QR算法的变体

QR算法是一个最成功的和强大的工具在数学软件。

MATLAB^®核心库包括几个不同的QR算法。这些变异计算实对称矩阵的特征值,实非对称矩阵,对真正的矩阵,复杂的矩阵,对复杂的矩阵,和各种类型的矩阵的奇异值。这些核心库函数用于各种MATLAB工具箱找到稀疏矩阵的特征值和奇异值和线性算子,找到多项式的零,解决特殊的线性系统,评估数值稳定性和执行其他任务。

几十人发展了QR算法的变体。第一个论文主题来自J.G.F.弗朗西斯在1961年和1962年,维拉在1963年联合国Kublanovskaya。但是是J.H.威尔金森发达的第一个完整实现QR算法。威尔金森也开发了一个重要的收敛性分析。威尔金森的书代数特征值问题和他的两个文件是出版于1965年。这意味着我们可以庆祝2015年黄金周年实用QR算法。

QR算法的变体使用奇异值分解(圣)发表在1965年由基因Golub Velvel卡亨和完善1969年由Golub基督教Reinsch。

“QR”这个名字

“QR”这个名字来源于字母Q正交矩阵,用来表示字母R,用来表示对三角矩阵。有一个qr在MATLAB函数,但它计算QR分解,不是QR算法。任何矩阵,是否真实的或复杂的,正方形或者矩形,可以分解成一个矩阵的乘积问与正交矩阵列和R只在上层的非零,或正确的,三角形。你可能还记得克施密特的过程,这也差不多,虽然在其原来的形式是数值不稳定。

一行程序

使用qrQR算法的函数,一个简单的变体可以表示一行的MATLAB代码。让一个是一个广场,n——- - - - - -n矩阵,让我眼睛= (n, n)。然后给出了迭代QR的一步

s = (n, n);(Q, R) = qr(*我);一个= R * Q + s *我

的数量\ \)转变;它加速收敛。\ \()方法一个上三角矩阵,\(\)方法一个特征值。如果你输入一行上的这三个语句,您可以使用向上箭头键进行迭代。

QR分解产生一个上三角\ (R \)。

\ [QR晶硅= \]

然后倒序乘法,\ (RQ \),恢复特征值,因为

中移动\ [+ sl =问^ {T} (sl) Q + sl = Q ^ {T} AQ \]

所以新的\(\)类似于原始\ (\)。每个迭代有效转移一些“质量”从下到上的三角形,同时保留特征值。随着迭代的进行,矩阵开始接近一个上三角矩阵的特征值方便地显示在对角线。

一个例子

来说明这一过程我们将使用一个矩阵从MATLAB美术馆收藏。

一个=画廊(3)= -149 -50 -154 537 180 546 -27 9 -25

它是不明显的,但是这个矩阵构造特征值1,2,3。我们一行的第一次迭代QR代码生成

一个= 28.8263 -259.8671 773.9292 1.0353 -8.6686 33.1759 -0.5973 5.5786 -14.1578

矩阵是现在更接近上三角,但特征值仍不明显。然而,在五个迭代

一个= 3.0321 -8.0851 804.6651 0.0017 0.9931 145.5046 -0.0001 0.0005 1.9749

我们开始看到特征值3,1和2新兴对角线上。八个迭代给

A = 3.0716 -7.6952 802.1201 0.0193 0.9284 158.9556 2.0000 0 0

特征值2.0已经计算显示的准确性,和相邻below-diagonal元素,已经成为零。在这一点上需要继续迭代2×2左上角子矩阵。

QR算法不会在这个简单的形式进行。之前总是减少到一个紧凑的形式,所有副斜杆下面的元素为零。迭代保留了这一简化型,分解可以更快地完成。的转变策略是更复杂的,是不同的各种形式的算法。此外,形式是至关重要的减少迭代的收敛性质。

对称矩阵

数字1 - 3说明QR算法的三个最重要的变量。从数据快照输出生成的程序eigsvdgui.m从与MATLAB数值计算。

最简单的变体涉及真实的,对称矩阵。一个n——- - - - - -n真实的,可以简化为三对角对称矩阵的形式n -户主倒影,序列相似性变换保留特征值。QR迭代适用于三对角形式。威尔金森转变策略,让他提供证明全局收敛性和局部立方收敛速度。即使在舍入误差的存在,这个算法是成功的保证。

图1显示了一个初始对称矩阵,情况中途减少三对角,三对角,半道上,QR迭代,最后,特征值。实际上,由于矩阵是对称的,计算是只执行一个一半的数组,但是我们的图反映了结果显示整个矩阵。

非对称矩阵

真实的情况,非对称矩阵要复杂得多。最初的减少使用n -户主相似转换来创建一个Hessenberg矩阵,这是上三角加上一个“额外的”副斜杆。一个迭代QR然后使用双转移战略。这种保存Hessenberg形式而试图创建一个真正舒尔的形式,这是上三角除了2×2块对应于双对角线上的共轭复数特征值。

非对称Hessenberg QR算法并不可靠。这是一个迭代的过程并不总是保证收敛。30年前,反例的基本迭代是已知的。威尔金森引入一个额外的“临时”转向处理它们,但是没有人能够证明一个完整的收敛定理。所以,在极少数情况下,MATLAB用户可能看到这个消息:

错误使用= = > eig,解决方案将不收敛

年前,此消息的接收者可能已经接受了这是不可避免的。但今天,大多数人都会感到惊讶或生气;他们所期望的绝对可靠。

现在我们知道可能导致实际的一个4×4例,非对称QR算法某些电脑上失败,即使威尔金森的特设的转变。矩阵是

\ [= \ {bmatrix}开始0 & 2 & 0 & 1 \ \ 1 & 0 & 0 & 0 \ \ 0 & 1 & 0 & 0 \ \ 0 & 0 & 1 & 0 \ {bmatrix}结束\]

这是同伴的矩阵多项式\ (p (x) = x ^ 4 - 2 x ^ 2 + 1 \),和声明

根((1 0 2 0 1))

要求的计算eig (A)。值\ \λ= 1 \和\(\λ= 1 \)都是特征值,或与多样性两个多项式的根,。真正\ (x \)多项式\ (p (x) \)从来不是消极的。这些双根减缓迭代,以至于,在一些电脑,变幻莫测的舍入误差影响收敛之前检测到。迭代可以永远游荡,试图收敛,但转个弯的时候关闭。

类似行为的例子所示的形式

\[开始\ {bmatrix} & 1 & 0 & 0 \ \ 1 & 0 & - \ & 0 \ \ 0 & \δ1 \ \ & 0 & 0 & 0 & 1 & 0 \ {bmatrix}结束\]

在\三角洲(\ \)neglected-say很小但不足够小,\ \(δ= 10 ^ {8}\)。的特征值接近的一对双根。威尔金森双重转变从每一对迭代使用一个特征值。这个迭代改变矩阵,但不足以得到快速收敛。所以我们必须使用一个不同的双重转变基于重复的一个特征值较低的2×2块。

这些不同的临时改变策略纳入LAPACK的最新版本,因此,MATLAB。我们现在的情况,我们不知道任何原因的矩阵eig或根显示“不收敛”消息,但是我们没有证明这些不同的修饰的非对称代码是可靠的。

图2显示了一个最初的非对称矩阵,情况中途减少Hessenberg形式,Hessenberg形式,经过迭代QR的中途,最后真正舒尔的形式。对于这个特殊的矩阵,它发生有四个实特征值和三个复杂的共轭双,总共十个特征值。

奇异值

可能矩形矩阵的奇异值\(\)对称矩阵的特征值的平方根\ (^ {T} \)。这一事实可以用来激励和分析一个算法,但是它不应该是实际计算和有限精度算法的基础。Golub-Kahan-Reinsch算法的初始阶段包括户主反射操作在左派和右派减少到两对角线矩阵的形式。这个阶段是紧随其后的是一个圣言两对角线QR算法的变异操作。威尔金森的分析对称三对角QR也适用于这个算法,所以这个过程是保证全局收敛的。

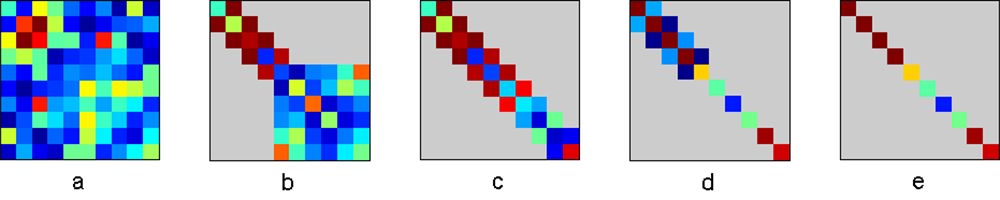
图3显示了初始长方形矩阵,情况中途减少两对角线形式,两对角线形式,经过迭代QR的中途,最后对角形式包含奇异值。

QR算法应用

虽然QR算法计算特征值和奇异值密切相关,结果的应用程序通常是非常不同的。特征值通常用来分析常微分方程组,行为作为时间的函数是非常重要的。奇异值,另一方面,是有用的分析静态系统的线性方程组,方程的数量通常是不一样的未知数的数目。

控制理论和控制设计自动化使大量使用特征值。经典控制理论中状态空间微分方程组的研究

{对齐}\ \[\开始点{x} & y = Ax +布鲁里溃疡\ \ & =残雪+ Du \{对齐}结束\]

使用QR算法计算的特征值\(\)等问题的调查是至关重要的稳定性和可控性。

在统计数据,计算数值可靠的方式获取的主要组件。主成分分析(PCA)是一种技术分析线性方程组的一个超定的系统

\ [Ax = b \]

\ \()行比列。使用QR算法计算的奇异值向量\(\)产生的主要组件。

为进一步阅读和观看

Golub基因H。查尔斯·f·范贷款,矩阵计算,第四版约翰·霍普金斯大学出版社,1996年,697页。

硅藻土、克里夫与MATLAB数值计算第十章,“特征值和奇异值”。

硅藻土、克里夫1976矩阵奇异值分解的电影。

威尔金森,J.H代数特征值问题牛津大学出版社,1965年,662页。