适应自定义分布
这个例子展示了如何使用自定义分布来适应单变量数据最大似然误差函数。
你可以使用最大似然误差函数来计算最大似然参数估计,并估计内置分布和自定义分布的精度。要适应自定义发行版,需要在文件中或使用匿名函数为自定义发行版定义函数。在最简单的情况下,您可以编写代码来计算您想要匹配的分布的概率密度函数(pdf)或pdf的对数,然后调用最大似然误差来适应分布。这个例子涵盖了以下使用pdf或pdf的对数的情况:
为截断数据拟合分布
拟合两个分布的混合
拟合加权分布
利用参数变换寻找小样本的参数估计的精确置信区间
请注意,您可以使用TruncationBounds的名称值参数最大似然误差对于截断的数据,而不是定义自定义函数。此外,对于两个正态分布的混合,可以使用fitgmdist作用此示例使用最大似然误差函数和自定义函数。
拟合零截断泊松分布
计数数据通常使用泊松分布建模,您可以使用poissfit或fitdist函数来拟合泊松分布。然而,在某些情况下,数据中没有记录为零的计数,因此,由于缺少零,拟合泊松分布并不简单。在这种情况下,拟合一个泊松分布到零截断数据最大似然误差函数和自定义分布函数。
首先,生成一些随机泊松数据。
rng(18,“旋风”)%为了再现性λ= 1.75;n = 75;x1 = poissrnd(λ,n, 1);
接下来,从数据中删除所有的零来模拟截断。
>: = cross (>);
检查中的样本数量x1后截断。
长度(x1)
ans=65
绘制模拟数据的直方图。
直方图(x1, 0:1:马克斯(x1) + 1)

数据看起来像泊松分布,只是不包含零。您可以使用与正整数上的泊松分布相同的自定义分布,但概率为零。通过使用自定义分布,您可以估计泊松参数兰姆达同时对缺失的零进行解释。
您需要通过概率质量函数(pmf)定义零截断泊松分布。创建一个匿名函数来计算每个点的概率x1,给定泊松分布的平均参数值兰姆达这个pmf for a zero-truncated Poisson distribution is the Poisson pmf normalized so that it sums to one. With zero truncation, the normalization is1–概率(x1<0)。
Pf_truncpoiss = @(x1,lambda) poisspdf(x1,lambda)./(1-poisscdf(0,lambda));
为简单起见,假设所有x1指定给此函数的值为正整数,不进行任何检查。对于错误检查或需要多行代码的更复杂的分发,必须在单独的文件中定义函数。
为参数找到一个合理的粗略猜测兰姆达。在这种情况下,使用样本均值。
开始=意味着(x1)
开始= 2.2154
提供最大似然误差使用数据、自定义pmf函数、初始参数值和参数的下限。由于泊松分布的平均参数必须为正,因此还需要为参数指定下限兰姆达这个最大似然误差函数返回函数的最大似然估计兰姆达,以及(可选)参数的近似95%置信区间。
[lambdaHat,lambdaCI]=mle(x1,“pdf”pf_truncpoiss,“开始”开始,...“LowerBound”,0)
lambdaHat=1.8760
兰巴奇=2×11.4990 2.2530
参数估计值小于样本平均值。最大似然估计值解释了数据中不存在的零。
或者,可以使用TruncationBounds名称值参数。
[lambdaHat2,lambdaCI2]=mle(x1,“分配”,“泊松”,...“TruncationBounds”[0正])
lambdaHat2=1.8760
lambdaCI2=2×11.4990 2.2530
您还可以计算的标准误差估计兰姆达通过使用mlecov。
avar=mlecov(λ,x1,“pdf”,pf_truncpois);标准偏差=sqrt(avar)
标准差=0.1923
要目视检查拟合,请根据原始数据的标准化直方图绘制拟合的pmf
直方图(x1,“正常化”,“pdf”) xgrid = min(x1):max(x1);pmfgrid = pf_truncpoiss (xgrid lambdaHat);持有在绘图(xgrid、pmfgrid、,“- - -”)包含(“x1”) ylabel (“概率”)传奇(样本数据的,“安装pmf”,“位置”,“最好的”)举行从

拟合上截断正态分布
连续数据有时会被截断。例如,由于数据收集的限制,大于某个固定值的观测值可能不会被记录。
在这种情况下,模拟截断正态分布的数据。首先,生成一些随机正态数据。
n=500;μ=1;σ=3;rng(“默认”)%为了再现性x2=正常值(μ,西格玛,n,1);
接下来,删除任何超出截断点的观测值xTrunc。假设xTrunc是一个您不需要估计的已知值。
xTrunc = 4;x2 = x2(x2 < xTrunc);
检查中的样本数量x2后截断。
长度(x2)
ans=430
创建模拟数据的柱状图。
直方图(x2)
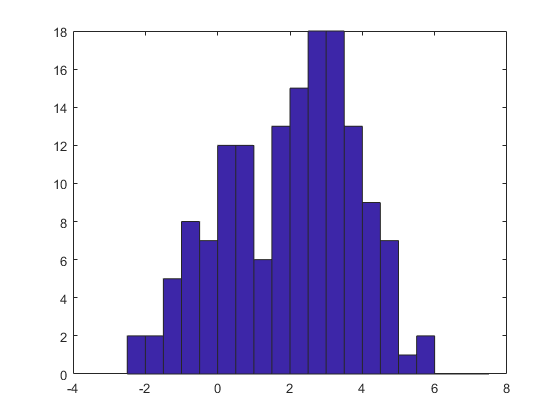
用与正态分布相同的自定义分布拟合模拟数据x2xTrunc。通过使用自定义分布,您可以估计正态参数μ和σ在解释丢失的尾巴时。
通过pdf定义截断正态分布。创建一个匿名函数,以计算x中每个点的概率密度值,给定参数值μ和σ。在截断点固定且已知的情况下,截断正态分布的pdf是截断后的pdf,然后进行归一化,以便将其集成到一个。归一化是在xTrunc。为简单起见,假设所有x2值小于xTrunc,没有检查。
pdf_truncnorm=@(x2,mu,sigma)...normpdf (x2,μ、σ)。/ normcdf (xTrunc、μ、σ);
因为不需要估计截断点xTrunc,它不包含在自定义PDF函数的输入分布参数中。xTrunc也不是数据向量输入参数的一部分。匿名函数可以访问工作区中的变量,因此您不必传递xTrunc将匿名函数作为附加参数。
为参数估计提供一个粗略的开始猜测。在这种情况下,因为截断不是极端的,所以使用样本平均值和标准偏差。
开始=[平均值(x2),标准值(x2)]
开始=1×20.1585 2.4125
提供最大似然误差使用数据、自定义pdf函数、初始参数值和参数的下限。因为σ必须为正,还需要指定参数下限。最大似然误差的最大似然估计μ和σ作为单个向量,以及两个参数的近似95%置信区间矩阵。
[参数,参数]=mle(x2,“pdf”pdf_truncnorm,“开始”开始,...“LowerBound”,[-Inf 0])
护理人员=1×21.1298 3.0884
paramCIs =2×20.5713 2.7160 1.6882 3.4607
的估计μ和σ大于样本平均值和标准偏差。模型拟合解释了分布缺失的上尾。
或者,可以使用TruncationBounds名称值参数。
[paramEsts2, paramCIs2] =大中型企业(x2,“分配”,“正常”,...“TruncationBounds”,[-Inf xTrunc])
paramEsts2 =1×21.1297 - 3.0884
paramCIs2 =2×20.5713 2.7160 1.6882 3.4607
可以使用计算参数估计的近似协方差矩阵mlecov这个approximation typically works well for large samples, and you can approximate the standard errors by the square roots of the diagonal elements.
acov = mlecov (paramEsts x2,“pdf”pdf_truncnorm)
acov =2×20.0812 0.0402 0.0402 0.0361
stderr =√诊断接头(acov))
stderr =2×10.2849 - 0.1900
要直观地检查拟合情况,请根据原始数据的标准化直方图绘制拟合pdf。
直方图(x2,“正常化”,“pdf”)xgrid=linspace(最小(x2),最大(x2));pdfgrid=pdf_truncnorm(xgrid,参数(1),参数(2));保持在情节(xgrid pdfgrid,“- - -”)包含(“x2”) ylabel (“概率密度”)传奇(样本数据的,“安装pdf”,“位置”,“最好的”)举行从

拟合两个正态分布的混合
一些数据集显示双模态,甚至多模态,用标准分布来拟合这些数据通常是不合适的。然而,简单的单峰分布的混合通常可以很好地模拟这样的数据。
在这种情况下,将两个正态分布的混合物拟合到模拟数据。
首先,掷一枚有偏见的硬币。
如果硬币正面朝上,从一个有均值的正态分布中随机选取一个值 和标准差 。
如果硬币落在背面,从一个有均值的正态分布中随机选择一个值 和标准差 。
从混合的学生信息生成数据集t而不是使用你拟合的相同模型。通过使用不同的分布(类似于在蒙特卡罗模拟中使用的技术),您可以测试拟合方法对偏离拟合模型假设的稳健程度。
rng(10)%为了再现性x3=[trnd(20,1,50)trnd(4,1100)+3];直方图(x3)

通过创建一个匿名函数来计算概率密度,定义适合的模型。两个正态分布的混合pdf是两个正态分量的pdf的加权和,由混合概率加权。匿名函数接受6个输入:一个用于评估pdf的数据向量和5个分布参数。每个分量都有其均值和标准差的参数。
pdf_normmixture = @ (x3, p, mu1、mu2 sigma1, sigma2)...p*normpdf(x3,mu1,sigma1)+(1-p)*normpdf(x3,mu2,sigma2);
您还需要对参数进行初步猜测。随着模型参数数量的增加,定义起点变得更加重要。在这里,从等量的混合物(p=0.5),以数据的两个四分位数为中心,具有相等的标准偏差。标准偏差的起始值来自混合物方差公式,即各成分的平均值和方差。
pStart = 5;muStart =分位数(x3,[。25。)
muStart =1×20.3351 - 3.3046
sigmaStart=sqrt(变量(x3)-.25*diff(muStart)。^2)
sigmaStart = 1.1602
start = [pStart muStart sigmaStart sigmaStart]; / /开始
为混合概率指定0和1的界限,为标准偏差指定0的下限。将边界向量的其余元素设置为+Inf或负,表示没有限制。
lb = [0 -Inf -Inf 0 0];ub = [1 Inf Inf Inf Inf];paramEsts =大中型企业(x3,“pdf”pdf_normmixture,“开始”开始,...“LowerBound”磅,“UpperBound”,ub)
警告:最大似然估计不收敛。迭代超过限制。
护理人员=1×50.3273 -0.2263 2.9914 0.9067 1.2059
警告消息表明该函数不收敛于默认迭代设置。显示默认选项。
斯塔塞特(“定制”)
ans =结构体字段:显示:'off'MaxFunEvals:400 MaxIter:200 TolBnd:1.0000e-06 TolFun:1.0000e-06 TolTypeFun:[]TolX:1.0000e-06 TolTypeX:[]GradObj:'off'Jacobian:[]DerivStep:6.0555e-06 FunValCheck:'on'Robust:[]RobustWgtFun:[]调谐:[]使用并行:[]使用子流:[]流:[]输出:[]
自定义发行版的默认最大迭代次数是200。控件创建的选项结构覆盖默认值以增加迭代次数斯塔塞特函数。此外,增加最大函数求值。
选项=statset(“MaxIter”, 300,“MaxFunEvals”,600); 参数=mle(x3,“pdf”pdf_normmixture,“开始”开始,...“LowerBound”磅,“UpperBound”,ub,“选项”,选项)
护理人员=1×50.3273 -0.2263 2.9914 0.9067 1.2059
最终的收敛迭代只在结果的最后几位有意义。然而,最佳实践是始终确保达到收敛。
为了直观地检查拟合情况,将拟合密度绘制到原始数据的概率直方图上。
直方图(x3,“正常化”,“pdf”)举行在xgrid = linspace(1.1 *分钟(x3), 1.1 *马克斯(x3), 200);pdfgrid = pdf_normmixture (xgrid,...参数(1)、参数(2)、参数(3)、参数(4)、参数(5));绘图(xgrid、pdfgrid、,“- - -”)举行从xlabel(“x3”) ylabel (“概率密度”)传奇(样本数据的,“安装pdf”,“位置”,“最好的”)
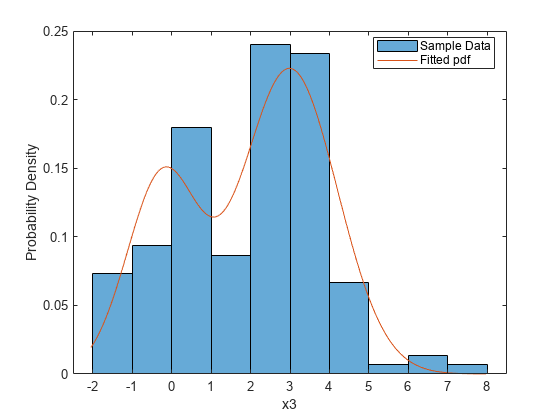
或者,对于正态分布的混合,可以使用fitgmdist函数。由于初始估计和迭代算法的设置,估计可能会有所不同。
Mdl = fitgmdist (x3 ', 2)
Mdl=一维两组分的高斯混合分布组分1:混合比例:0.329180平均值:-0.2200组分2:混合比例:0.670820平均值:2.9975
Mdl。σ
Ans = Ans (:,:,1) = 0.8274
对精度不等的数据拟合加权正态分布
假设你有10个数据点,每个数据点实际上是1到8个观测值的平均值。原始的观测数据是不存在的,但是每个数据点的观测数据的数量是已知的。每个点的精度取决于其相应的观测数。你需要估计原始数据的均值和标准差。
X4 = [0.25 -1.24 1.38 1.39 -1.43 2.79 3.52 0.92 1.44 1.26]';M = [8 2 1 3 8 4 2 5 2 4]';
每个数据点的方差与其相应的观测次数成反比,因此使用1/m以最大似然拟合对每个数据点的方差进行加权。
w=1./m;
在这个模型中,您可以通过pdf定义分发版。但是,使用对数格式的pdf更合适,因为普通的pdf有这种形式
C .* exp(-0.5 .* z.^2),
和最大似然误差获取PDF的日志以计算日志可能性。因此,创建一个直接计算pdf对数的函数。
pdf函数的对数必须计算中每个点的概率密度的对数x,给出正态分布参数μ和σ. 它还需要考虑不同的方差权重。定义一个名为助手日志PDF\U wn1单独归档helper\u logpdf\u wn1.m。
函数逻辑=helper\u logpdf\u wn1(x,m,mu,sigma)%HELPER_LOGPDF_WN1权重正态分布的pdf的对数%这个函数只支持Fit Cust金宝appom Distributions示例% (customdist1demo.mlx),并可能在未来的版本中更改。v =σ。^ 2。/ m;呆呆的= - (xμ)。^2 ./ (2.*v) - 5.*log(2.*pi.*v);结束
为参数估计提供粗略的初步猜测。在这种情况下,使用未加权样本平均值和标准偏差。
开始=[平均值(x4),标准值(x4)]
开始=1×21.0280 1.5490
因为σ必须是正的,需要指定参数的下界。
[paramEsts1, paramCIs1] =大中型企业(x4,“logpdf”,...@(x,mu,sigma)helper_logpdf_wn1(x,m,mu,sigma),...“开始”开始,“LowerBound”,[-Inf,0])
paramEsts1 =1×20.6244 2.8823
paramCIs1 =2×2-0.2802 1.6191 1.5290 4.1456
估计μ小于样本平均值估计值的三分之二。估计受最可靠的数据点的影响,即基于最大原始观测数的点。在该数据集中,这些点倾向于将估计值从未加权样本均值中拉低。
利用参数变换拟合正态分布
的最大似然误差函数计算参数的置信区间使用大样本正态逼近的分布的估计,如果一个精确的方法是不可得的。对于小样本容量,可以通过转换一个或多个参数来改进正态逼近。在这种情况下,将正态分布的比例参数转换为其对数。
首先,定义一个名为助手日志PDF\U wn2使用转换后的参数σ。
函数logy=helper\u logpdf\u wn2(x,m,mu,logsigma)%HELPER_LOGPDF_WN2为权重正态分布的pdf的对数%日志(σ)参数化%这个函数只支持Fit Cust金宝appom Distributions示例% (customdist1demo.mlx),并可能在未来的版本中更改。v = exp (logsigma)。^ 2。/ m;呆呆的= - (xμ)。^2 ./ (2.*v) - 5.*log(2.*pi.*v);结束
使用转换为新参数化的相同起始点σ,即样本标准差的对数。
开始=[平均值(x4),对数(标准值(x4))]
开始=1×21.0280 - 0.4376
因为σ可以是任何正值,对数(西格玛)是无界的,不需要指定下界或上界。
[参数2,参数2]=mle(x4,“logpdf”,...@ (x,μ、σ)helper_logpdf_wn2 (x, m,μ、σ),...“开始”,开始)
paramEsts2 =1×20.6244 1.0586
paramCIs2 =2×2-0.2802 0.6203 1.5290 1.4969
因为参数化使用对数(西格玛),您必须转换回原始比例,以获得的估计值和置信区间σ。
sigmaHat=exp(参数2(2))
sigmaHat=2.8823
sigmaCI = exp (paramCIs2 (:, 2))
sigmaCI =2×11.8596 4.4677
两者的估计μ和σ与第一次拟合相同,因为最大似然估计对参数化是不变的σ稍微不同于参数1(:,2)。

