函数导数教程

打开直播脚本

此示例演示如何在符号数学工具箱中使用函数导数™ 以波动方程为例。本例以符号方式进行计算，以获得分析结果。固定在两端的弦的波动方程使用函数导数进行求解。函数导数是函数相对于函数所依赖函数的导数。符号数学工具箱™ 使用功能性动机作用

波动方程的求解是泛函导数的一个应用。它描述了波的运动，从弦的运动到电磁波的传播，是物理学中的一个重要方程。你可以将本例中说明的技术应用于从求解短杆方程到变分法中的应用ochrone问题用于寻找肥皂泡的最小表面。

考虑一串长度L暂停在两点之间x = 0.和x = L..该弦每单位长度具有特征密度和特征张力。定义后来使用的常量长度，密度和张力。为简单起见，将这些常量设置为1..

长度= 1;密度= 1;张力= 1;

如果弦在运动，弦的动能和势能是其相对于静止位移的函数s（x，t），它随位置而变化x时间呢T如果D是单位长度的密度，动能是

$T = \int_{0}^{L} \frac{D}{2.} {(\frac{D}{D T} s (x, T))}^{2.} D x .$

势能是

$v = \int_{0}^{L} \frac{R}{2.} {(\frac{D}{D x} s (x, T))}^{2.} D x,$

哪里R是紧张。

在MATLAB®中输入这些等式。由于长度必须是正的，因此设置了这个假设。这个假设允许简化将结果方程简化为预期形式。

符号s（x，t）DRvL假设（L> 0）T（x，t）= int（d / 2 * diff（s，t）^ 2，x，0，l）;v（x，t）= int（r / 2 * diff（s，x）^ 2，x，0，l）;

那个行动A.是电视.最小行动的原则指出，该行动总是最小化。通过找到功能衍生物来确定最小动作的条件A.关于s使用功能性动机并将其等同于零。

A=T-V；方程n=函数驱动（A，S）==0

EQN（x，t）=
                
                  $L R \frac{\partial^{2.}}{\partial x^{2.}} s (x, T) - L D \frac{\partial^{2.}}{\partial T^{2.}} s (x, T) = 0$

使用简化.将方程式转换为其预期形式，替换为研发与波速的平方成正比v.

EQN =简化（EQN）/ R;EQN =子（EQN，R / D，V ^ 2）

EQN（x，t）=
                
                  $\frac{\frac{\partial^{2.}}{\partial T^{2.}} s (x, T)}{v^{2.}} = \frac{\partial^{2.}}{\partial x^{2.}} s (x, T)$

用分离变量的方法求解方程S（x，t）=U（x）*V（t）分离对位置的依赖x时间呢T.使用以下方法分离所得等式的两侧：孩子们.

符号U（x）V（t）eqn2=subs（eqn，S（x，t），U（x）*V（t））；eqn2=eqn2/（U（x）*V（t））

方程n2（x，t）=
                
                  $\frac{\frac{\partial^{2.}}{\partial T^{2.}} v (T)}{v^{2.} v (T)} = \frac{\frac{\partial^{2.}}{\partial x^{2.}} U (x)}{U (x)}$

TMP =儿童（EQN2）;

等式的两侧依赖于不同的变量，但却是相等的。只有在每一侧是常数，才有可能。将每一侧等同于任意常数C得到两个微分方程。

符号C方程n3=tmp（1）==C

eqn3 =
                
                  $\frac{\frac{\partial^{2.}}{\partial T^{2.}} v (T)}{v^{2.} v (T)} = C$

方程n4=tmp（2）==C

方程4=
                
                  $\frac{\frac{\partial^{2.}}{\partial x^{2.}} U (x)}{U (x)} = C$

使用求解微分方程Dsolve.在位移为0在x = 0.和t = 0..使用以下公式将方程简化为其预期形式：简化与之脚步选项设置为50.

v（t）= dsolve（eqn3，v（0）== 0，t）;u（x）= dsolve（eqn4，u（0）== 0，x）;v（t）=简化（v（t），'脚步'，50）

v（t）=
                 $- 2. C_{1.} 信义 (\sqrt{C} T v)$

U（x）=简化（U（x），'脚步'，50）

U（x）=
                 $2. C_{1.} 信义 (\sqrt{C} x)$

获得方程中的常数。

p1 = setdiff（symvar（u（x）），sym（[c，x]））

P1 =
                 $C_{1.}$

p2=setdiff（symvar（V（t）），sym（[C，V，t]））

p2 =
                 $C_{1.}$

绳子固定在两个位置x = 0.和x = L..条件U（0）= 0已存在。请应用U（L）=0并解决C.

eqn_bc = u（l）== 0;[solc，param，cond] =解决（eqn_bc，c，“返回条件”，对）

索尔克=
                
                  $- \frac{K^{2.} {π.}^{2.}}{L^{2.}}$

param =
                 $K$

Cond =.
                 $K \in Z \land C_{1.} \neq 0 \land 1. \leq K$

假设（Cond）

解决方案s（x，t）是U（x）和V（t）.找到解决方案，并将字符串的特征值替换为解决方案以获得解决方案的最终形式。

S（x，t）=U（x）*V（t）；S=subs（S，C，solC）；S=subs（S[lv]，[长度sqrt（张力/密度）]；

参数P1和P2.确定振动的幅度。放P1和P2.到1.为了简单起见。

S=subs（S，[p1p2]，[11]）；S=简化，'脚步'，50）

s（x，t）=
                 $4. 罪 (π. K T) 罪 (π. K x)$

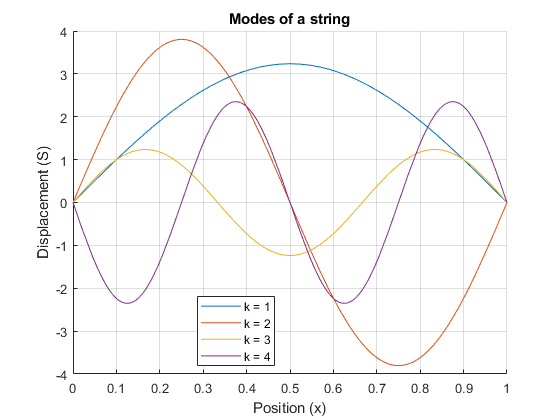
对于不同的振动值，弦具有不同的振动模式K.绘制任意时间值的前四种模式T.使用param由返回的参数解决要解决参数K.

Splot（x）=S（x，0.3）；图（1）保持在网格在ymin=双（系数（Splot））；对于i=1:4 yplot=subs（Splot，参数，i）；fplot（yplot，[0长度]）终止ylim（[ -  ymin ymin]）传奇（'k = 1','k = 2','k = 3','k = 4','地点',“最好的”）Xlabel（‘位置（x）’）ylabel（'流离失所（s）'） 标题（'字符串的模式')

图包含轴对象。具有字符串的标题模式的轴对象包含4个函数线的4个对象。这些对象表示k = 1，k = 2，k = 3，k = 4。

波动方程是线性的。这意味着允许模式的任何线性组合是波动方程的有效解决方案。因此，具有给定边界条件和初始值的波动方程的完整解决方案是允许模式的总和

$F (x, T) = \sum_{K = N}^{M} {A.}_{K} 罪 (π. K T) 罪 (π. K x),$

哪里 ${A.}_{K}$ 表示任意常数。

用Symsum.将字符串的前五个模式相加。在一个新图形上，在与先前波形相同的时刻显示生成的波形，以进行比较。

图（2）S5（x）=1/5*symsum（S，参数，1,5）；fplot（子部件（S5，t，0.3），[0长度]）ylim（[-ymin-ymin]）网格在Xlabel（‘位置（x）’）ylabel（'流离失所（s）'） 标题（“前5种模式之和”)

图包含轴对象。具有前5个模式的标题求和的轴对象包含类型函数线的对象。

该图显示求和模式允许您对不同的波形进行定性建模 $s (x, T = 0) = 0$ 总的来说 $x$ .

您可以计算值 ${A.}_{K}$ 在等式中 $F (x, T) = \sum_{K = N}^{M} {A.}_{K} 罪 (π. K T) 罪 (π. K x)$ 通过指定初始速度的条件

$U_{T} (x, T = 0) = F_{T} (x, 0) .$

模式的适当总和可以表示任何波形，这与使用傅里叶级数表示字符串的运动相同。

函数导数教程

符号数学工具箱文档

金宝app

用符号数学工具箱进行数学建模