拉普拉斯算子的特征值

这个例子展示了如何解决拉普拉斯算子的特征值问题在一个l型地区。

膜的问题

考虑一个膜,是固定的边界 $\partial Ω$ 的一个地区 $Ω$ 在平面上。它的位移 $u (x, y)$ 是所描述的特征值问题 $Δ u = λ u$ ,在那里 $Δ u = u_{x x} + u_{y y}$ 拉普拉斯算子和吗 $λ$ 是一个标量参数。边界条件是 $u (x, y) = 0$ 对所有 $(x, y) \in \partial Ω$ 。

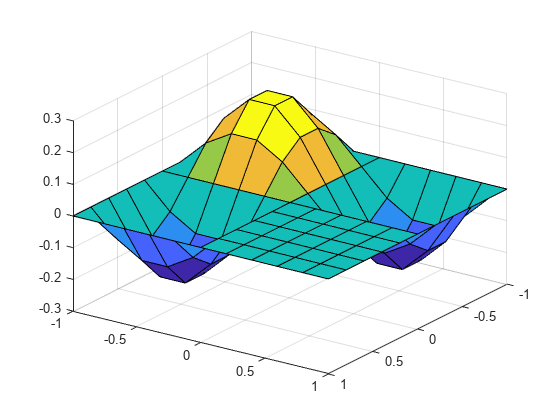
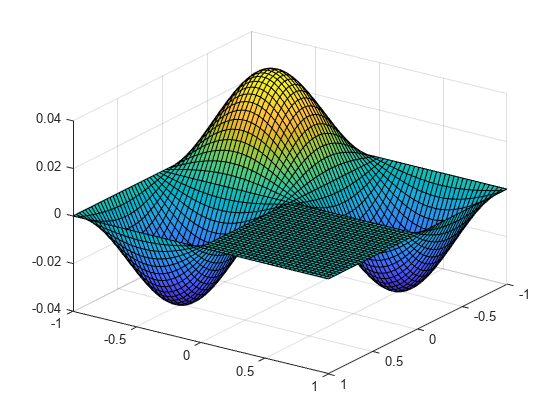
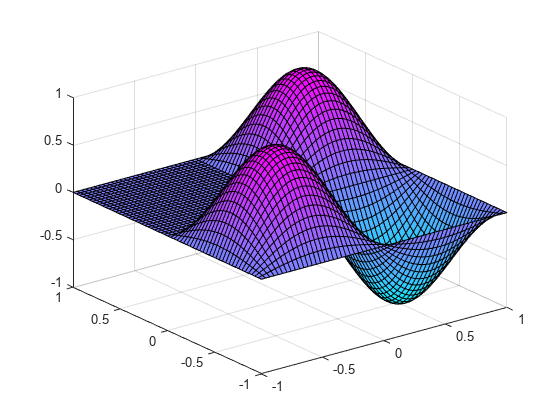
拉普拉斯算子自伴的和消极的,也就是说,只有真正的负特征值 $λ$ 存在。有一个最大的(负面)离散特征值,相应的本征函数 $u$ 被称为基态。在这个例子中, $Ω$ 是一个l型地区,基态与这个地区的l型膜MATLAB®商标。

9分有限差分近似

最简单的方法是近似拉普拉斯算子的特征值问题 $Δ u$ 由有限差分逼近(a钢网在正方形网格点的距离hx在 $x$ 方向和距离沪元在 $y$ 方向。在这个例子中,近似 $Δ u$ 用一笔S_h九个正则网格点的中点 $(x, y)$ 。未知的权重 ${一个}_{- - - - - - 1 - - - - - - 1}, \dots, {一个}_{11}$ 。

信谊u (x, y)每股收益a11a10a1_1a01a00a0_1a_11a_10a_1_1信谊hx沪元积极的S_h = a_11 * u (x - Eps * hx y + Eps * hy) +…a01 * u (x, y + Eps *沪元)+…a11 * u (x + Eps * hx y + Eps * hy) +…a_10 * u (x - Eps * hx, y) +…a00 * u (x, y) +…a10 * u (x + Eps * hx y) +…a_1_1 * u (x - Eps * hx y - Eps *沪元)+…a0_1 * u (x, y - Eps *沪元)+…a1_1 * u (x + Eps * hx y - Eps *衔接);

使用符号参数每股收益将这个表达式的权力的扩张hx和沪元。知道重量,可以近似的拉普拉斯算子的设置每股收益= 1。

t =泰勒(S_h,每股收益,“秩序”7);

使用多项式系数函数来提取它们的系数与相同的权力每股收益。包含的每个系数表达式hx,沪元和衍生品u关于 $x$ 和 $y$ 。自S_h代表 $u_{x x} + u_{y y}$ ,所有其他衍生品的系数u必须是零。提取系数代替所有的衍生品u,除了 $u_{x x}$ 和 $u_{y y}$ ,0。取代 $u_{x x}$ 和 $u_{y y}$ 1。这减少了泰勒展开式系数计算,并导致以下六个线性方程。

C =公式(多项式系数(t,每股收益,“所有”));eq0 =潜艇(C (7), u (x, y), 1) = = 0;eq11 =潜艇(C (6), (diff (u, x) diff (u, y)], [1,0]) = = 0;eq12 =潜艇(C (6), (diff (u, x) diff (u, y)], [0,1]) = = 0;eq21 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [1, 0, 0)) = = 1;eq22 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [0, 1,0]) = = 0;eq23 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [0, 0, 1]) = = 1;

因为有九个未知权重S_h,添加进一步要求所有三阶导数的方程u都是0。

eq31 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [1, 0, 0, 0) = = 0;eq32 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0 1 0,0]) = = 0;eq33 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0, 0, 1, 0]) = = 0;eq34 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0, 0, 0, 1]) = = 0;

解决由此产生的十个九个未知权重方程。使用ReturnConditions找到所有的解决方案包括任金宝搏官方网站意参数。

(a11 a10, a1_1、a01 a00、a0_1, a_11, a_10, a_1_1,参数、条件)=…解决([eq0, eq11、eq12 eq21, eq22, eq23, eq31, eq32, eq33, eq34),…(a11 a10, a1_1、a01 a00、a0_1, a_11, a_10, a_1_1),…“ReturnConditions”,真正的);扩大([a_11 a01, a11;…a_10、a00 a01;…a1_1、a0_1 a_1_1])

ans =
                  
                    $(\begin{array}{c} z & \frac{1}{{沪元}^{2}} - - - - - - 2 z & z \\ \frac{1}{{hx}^{2}} - - - - - - 2 z & 4 z - - - - - - \frac{2}{{hx}^{2}} - - - - - - \frac{2}{{沪元}^{2}} & \frac{1}{{沪元}^{2}} - - - - - - 2 z \\ z & \frac{1}{{沪元}^{2}} - - - - - - 2 z & z \end{array})$

参数

参数=
                   $z$

使用潜艇函数来代替权重计算的值。

C =简化(潜艇(C));

的表情C (7),C (6),C (4)包含第0、1和3的衍生品u消失。

[C (7)、C (6)、C (4))

ans =
                   $(\begin{array}{c} 0 & 0 & 0 \end{array})$

表达式C (5)的拉普拉斯算子u。

C (5)

ans =
                  
                    $\frac{\partial^{2}}{\partial x^{2}} u (x, y) + \frac{\partial^{2}}{\partial y^{2}} u (x, y)$

因此,在上面的值权重的计算中,模板S_h接近拉普拉斯算子的秩序hx ^ 2,hy ^ 2对于任何任意参数的值z,前提是z选择的顺序O (1 / hx ^ 2, 1 / hy ^ 2)。

包含第四和高阶导数

尽管解决方案包含一个自由参数z,该表达式C (3)包含四阶的导数u不能变成零的一个合适的选择z。另一个选择是把它变成一个多平方的拉普拉斯算子。

信谊d拉普拉斯= @ (u)拉普拉斯算子(u (x, y));扩大(d *拉普拉斯(拉普拉斯(u)))

ans (x, y) =
                  
                    $d \frac{\partial^{4}}{\partial x^{4}} u (x, y) + 2 d \frac{\partial^{2}}{\partial y^{2}} \frac{\partial^{2}}{\partial x^{2}} u (x, y) + d \frac{\partial^{4}}{\partial y^{4}} u (x, y)$

ans =

$\frac{{hx}^{2}}{12} = d$

ans =

{hx}^{2} {沪元}^{2} z = 2 d

ans =

$\frac{{沪元}^{2}}{12} = d$

ans =

$(\begin{array}{c} \frac{1}{360年} & h & h & h & h & \frac{\partial^{6}}{\partial x^{6}} u (x, y) + 5 \frac{\partial^{2}}{\partial y^{2}} \frac{\partial^{4}}{\partial x^{4}} u (x, y) + 5 \frac{\partial^{4}}{\partial y^{4}} \frac{\partial^{2}}{\partial x^{2}} u (x, y) + \frac{\partial^{6}}{\partial y^{6}} u (x, y) \end{array})$

ans (x, y) =

$\frac{\partial^{6}}{\partial x^{6}} u (x, y) + 3 \frac{\partial^{2}}{\partial y^{2}} \frac{\partial^{4}}{\partial x^{4}} u (x, y) + 3 \frac{\partial^{4}}{\partial y^{4}} \frac{\partial^{2}}{\partial x^{2}} u (x, y) + \frac{\partial^{6}}{\partial y^{6}} u (x, y)$

u (: 1) = 0;%左边界u (1) = 0;%下边界u(1:纽约,Nx) = 0;%对边界,上部u(纽约:纽约,nx) = 0;%对边界,下部u (Ny, 1: nx) = 0;%上限,剩下的部分nx u(纽约:nx) = 0;%上边界,对部分

u =

$(\begin{array}{c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & u_{2, 2} & u_{2, 3} & u_{2, 4} & u_{2, 5} & u_{2, 6} & u_{2, 7} & u_{2, 8} & u_{2, 9} & u_{2, 10} & 0 \\ 0 & u_{3, 2} & u_{3, 3} & u_{3, 4} & u_{3, 5} & u_{3, 6} & u_{3, 7} & u_{3, 8} & u_{3, 9} & u_{3, 10} & 0 \\ 0 & u_{4, 2} & u_{4, 3} & u_{4, 4} & u_{4, 5} & u_{4, 6} & u_{4, 7} & u_{4, 8} & u_{4, 9} & u_{4, 10} & 0 \\ 0 & u_{5, 2} & u_{5, 3} & u_{5, 4} & u_{5, 5} & u_{5, 6} & u_{5, 7} & u_{5, 8} & u_{5, 9} & u_{5, 10} & 0 \\ 0 & u_{6, 2} & u_{6, 3} & u_{6, 4} & u_{6, 5} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & u_{7, 2} & u_{7, 3} & u_{7, 4} & u_{7, 5} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & u_{8, 2} & u_{8, 3} & u_{8, 4} & u_{8, 5} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & u_{9, 2} & u_{9, 3} & u_{9, 4} & u_{9, 5} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & u_{10, 2} & u_{10, 3} & u_{10, 4} & u_{10, 5} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array})$

n =长度(var);陆=符号(0 (n, 1));为k = 1: n i =我(k);j = (k);陆(k) = 1/6 * u (i + 1, j - 1) + 2/3 * u (i + 1, j) + 1/6 * u (i + 1, j + 1)…+ 2/3 * u (i, j - 1) - 10/3 * (i, j) + 2/3 * u (i, j + 1)…j - 1 + 1/6 * u(张)+ 2/3 * u(张,j) + 1/6 *(张,j + 1);结束陆=陆/ hx ^ 2;

ans =

(\begin{array}{c} - - - - - - 9.5214641572625960021345709535953 & - - - - - - 14.431096242107969492574666743957 & - - - - - - 18.490392088545609858994660377955 \end{array})

μ=

- - - - - - 18.490392088545609858994660377955

λ=

- - - - - - 19.796765119155672176257649532142

xmin = 1;xmax = 1;ymin = 1;ymax = 1;nx = 30;Nx = 2 * nx-1;hx = (xmax-xmin) / (Nx-1);纽约= 30;纽约= 2 * ny-1;hy = (ymax-ymin) / (Ny-1); u = ones(Ny,Nx); u(:,1) = 0;%左边界u(1:纽约,Nx) = 0;%对边界,上部u(纽约:纽约,nx) = 0;%对边界,下部u (1) = 0;%下边界u (Ny, 1: nx) = 0;%上限,剩下的部分nx u(纽约:nx) = 0;%上边界,对部分u(纽约+ 1:纽约,nx + 1: nx) = 0;(I, J) =找到(u ~ = 0);n =长度(我);S_h =稀疏(n, n);为k = 1: n i =我(k);j = (k);S_h (k,我= = + 1 & J = = + 1) = 1/6;S_h (k,我= = + 1 & J = =) = 2/3;S_h (k,我= = + 1 & J = = J - 1) = 1/6;S_h (k,我= = & J = = + 1) = 2/3;S_h (k,我= = & J = =) = 10/3;S_h (k,我= = & J = = J - 1) = 2/3;张S_h (k,我= = & J = = + 1) = 1/6;张S_h (k,我= = & J = =) = 2/3; S_h(k,I==i-1 & J==j-1)= 1/6;结束S_h = S_h. / hx ^ 2;

另请参阅

功能

拉普拉斯算子的特征值

膜的问题

9分有限差分近似

包含第四和高阶导数

总结

使用符号矩阵来解决特征值问题

使用双精度矩阵来解决特征值问题

另请参阅

功能