ベ@ @ズの推論

ベイズの推論は,モデルまたはモデルパラメーターについての予備知識を取り込んで統計モデルを解析する処理です。このような推論の根底にあるのは，ベ。

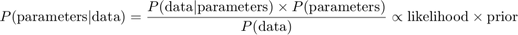
たとえば，次のような正規の観測値があるとします。

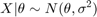
ここでsigmaは既知でありの予備知識は次のとおりです。

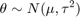
この式で，“ハパパラメタ”と呼ばれることもあるmuとtauも既知です。Xのn個の標本が観測される場合，次のようなthetaの事後分布を得ることができます。

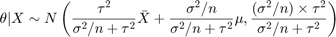
Thetaの事前分布，尤度分布，および事後分布を次のグラフに示します。

rng (0,“旋风”);N = 20;Sigma = 50;X = normrnd(10,sigma,n,1);Mu = 30;Tau = 20;Theta = linspace(- 40,100,500);Y1 = normpdf(mean(x)，theta,sigma/√(n));Y2 = normpdf(theta,mu,tau);postMean =τ^ 2 *意味着(x) /(τ)^ 2 +σ^ 2 / n) +σ^ 2 *亩/ n /(τ)^ 2 +σ^ 2 / n); postSD = sqrt(tau^2*sigma^2/n/(tau^2+sigma^2/n)); y3 = normpdf(theta, postMean,postSD); plot(theta,y1,“- - -”θ,y2,“——”,θ,y3,“-”。)传说(“可能性”，“之前”，“后”)包含(‘\θ)

自動車実験デ，タ

前に示した正規平均推定の例などの単純な問題では，閉じた形での事後分布を理解するのは簡単です。しかし,非共役事前分布が関係する一般的な問題では,事後分布を解析的に計算するのは困難または不可能です。そこで，例としてロジスティック回帰を検討します。この例には,燃費テストで不合格になった,さまざまな重量の自動車の割合をモデル化するのに役立つ実験が含まれています。デ，タには，重量，テストした自動車の台数，および不合格台数の観測値が含まれています。重量を変換して，回帰パラメ，タ，推定における相関を低減させます。

一套汽车砝码重量= [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';重量= (Weight -2800)/1000;%重新集中和缩放每种重量测试的汽车数量。%Total = [48 42 31 34 31 21 23 23 21 16 17 21]';在每个重量下，每加仑行驶里程表现不佳的汽车数量。%Poor = [1 2 0 3 8 8 14 17 19 15 17 21]';

ロジスティック回帰モデル

ロジスティック回帰は,一般化線形モデルの特殊ケースであり,応答変数が2項なのでここで示したデータにとって適切です。ロジスティック回帰モデルを次のように記述することができます。

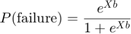
ここで，Xは計画行列で，bはモデルパラメ，タ，を格納したベクトルです。Matlab®では，この式を次のように記述できます。

logitp = @ (b, x) exp (b(1) +(2)。* x) / (1 + exp (b(1) +(2)。* x));

予備知識または無情報事前分布がある場合には,モデルパラメーターの事前確率分布を指定することができます。たとえば，この例では，截取パラメ，タ，b1とslopeパラメ，タ，b2に正規事前分布を使用します。まり，次のようになります。

Prior1 = @(b1) normpdf(b1,0,20);截距先验%Prior2 = @(b2) normpdf(b2,0,20);斜率先验%

ベズの定理により，モデルパラメタの結合事後分布は，尤度と事前分布の積に比例します。

Post = @(b) prod(binopdf(poor,total,logitp(b,weight)))).．.%的可能性* prior1(b(1)) * prior2(b(2));%先验

このモデルにおける事後分布の正規化定数は，解析的に処理しにくいことに注意してください。ただし,正規化定数が不明である場合でも,モデルパラメーターのおおよその範囲が既知であれば,事後分布を可視化することはできます。

B1 = linspace(-2.5， - 1,50);B2 = linspace(3, 5.5, 50);Simpost = 0 (50,50);为I = 1:长度(b1)为j = 1:长度(b2) simpost后(i, j) = ((b1(我),b2 (j)]);结束；结束；网格(b2, b1, simpost)包含(“坡”) ylabel (“拦截”) zlabel (“后验密度”)视图(-110,30)

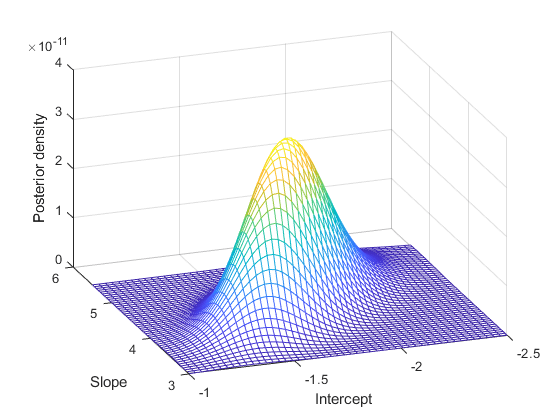
この事後分布は，パラメ，タ，空間内で対角線方向に延ばされています。これは，デ，タを調べた結果，パラメ，タ，が相関していると思われることを示しています。これは興味深いことです。なぜなら，デ，タを収集する前は，独立しているものと想定していたからです。この相関は，事前分布と尤度関数を組み合わせたことに由来します。

スラ@ @スサンプリング

デタのベズ解析では，事後分布を集計するためにモンテカルロ法がよく使用されます。これは,事後分布を解析的に計算できない場合でも,分布から無作為標本を生成し,このランダムな値を使用して事後分布または派生統計量(事後分布の平均値,中央値,標準偏差など)を推定できるという考え方です。スラ@ @スサンプリングは、比例定数 (これはまさに、正規化定数が未知である解析しにくい事後分布から標本を抽出するために必要とされるものです) までしかわかっていないときに、任意の密度関数を使用して分布から標本を抽出することを目的とするアルゴリズムの一種です。このアルゴリズムでは、独立した標本は生成されず、定常分布が対象の分布であるマルコフ系列が生成されます。このように、スライス サンプラーは、マルコフ連鎖モンテ カルロ (MCMC) アルゴリズムの一種です。ただし、スライス サンプラーは、よく知られている他の MCMC アルゴリズムとは異なります。指定する必要があるのは、スケーリングされた事後分布だけであるからです。提案分布と周辺分布を指定する必要はありません。

スライスサンプラーを燃費テストのロジスティック回帰モデルのベイズ解析の一部として使用する方法を次の例に示します。これには,モデルパラメーターの事後分布から無作為標本を生成し,サンプラーの出力を解析し,モデルパラメーターについて推定を行うことも含まれます。最初の手順は乱数標本を生成することです。

Initial = [1 1];Nsamples = 1000;Trace = slicesample(initial,nsamples，“pdf”的帖子,“宽度”20 [2]);

サンプラ，出力の解析

スラ。これは,その標本が,対象の事後分布から得られる無作為の実現の集合として妥当に処理され得るかどうかを判断するためです。出力を調べる最も簡単な方法は，周辺のトレ，スプロットを確認することです。

Subplot (2,1,1) plot(trace(:，1))“拦截”);Subplot (2,1,2) plot(trace(:，2)) ylabel(“坡”);包含(的样本数量);

これらのプロットから,50件ほどの標本でパラメーターの開始値の影響が消えて,プロセスが変動しないように見えるまでにしばらく時間がかかることは明らかです。

また,収束の有無を確認する際に,移動ウィンドウを使用して統計量(標本の平均値,中央値,標準偏差など)を計算することも役に立ちます。これにより,生のサンプルトレースより滑らかなプロットが得られるので,非定常性の識別と理解が簡単になります。

Movavg = filter((1/50)*ones(50,1)， 1, trace);Subplot (2,1,1) plot(movavg(:，1)) xlabel(“样本数量”) ylabel (“拦截手段”);Subplot (2,1,2) plot(movavg(:，2)) xlabel(“样本数量”) ylabel (“斜率均值”);

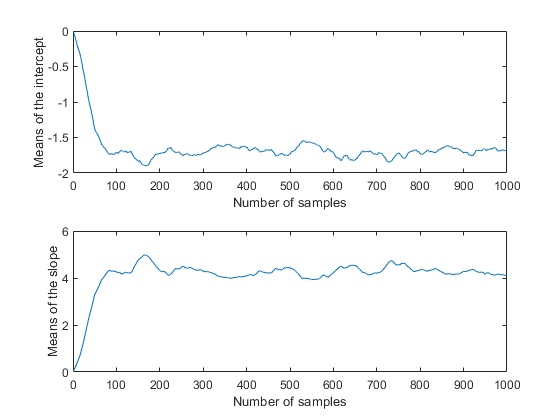
これらは,反復回数50回の間の移動平均なので,最初の50個の値はプロットのその他の値とは比較できません。ただし,各プロットの残りは,パラメーターの事後平均が100回ほどの反復の後に定常性に収束したことを裏づけているように思われます。また2つのパラメーターが,事後密度の前のプロットに一致して相互に相関し合っていることも明らかです。

沈静化期間の標本は対象の分布から得られる無作為の実現として適切には処理できないため,スライスサンプラーの出力の最初の50個ほどの値は使用しないことをお勧めします。単にそれらの出力行を削除することもできますが，“バンン”期間を指定することも可能です。これは、適切なバ、ン、ン長が(以前の実行例から)、既にわかっている場合に便利です。

Trace = slicesample(initial,nsamples，“pdf”的帖子,.．.“宽度”20 [2],“燃烧”, 50);Subplot (2,1,1) plot(trace(:，1))“拦截”);Subplot (2,1,2) plot(trace(:，2)) ylabel(“坡”);

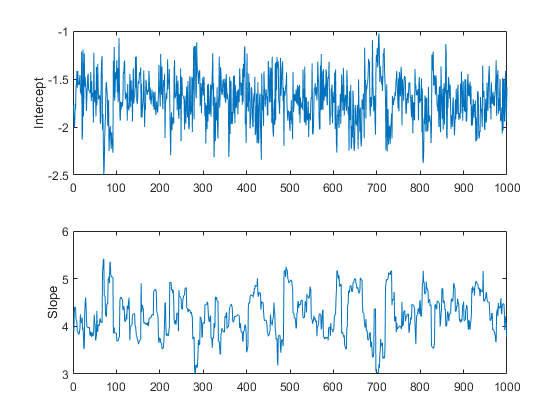
これらのトレースプロットは,非定常性を示しているようには見えず,バーンイン期間が自己の仕事を完了したことを示しています。

ただし，トレ，スプロットには別の面があり，これも調査する必要があります。拦截パラメーターのトレースが高周波ノイズのように見えるのに対して,斜率パラメーターのトレースの周波数成分は比較的低いようです。これは，隣接する反復箇所で値間に自己相関があることを示します。この自己相関標本から平均値を計算することはできますが,標本内の冗長部分を取り除いて,必要とされるストレージを下げると都合が良い場合がよくあります。これにより自己相関が排除された場合には,これを複数の独立値で構成される標本として扱うこともできます。たとえば10個に1個の比率で10番目の値だけを残すことにより,標本を減らすことができます。

Trace = slicesample(initial,nsamples，“pdf”的帖子,“宽度”20 [2],.．.“燃烧”, 50岁,“薄”10);

この間引きの効果を確認するには,標本の自己相関関数をトレースから推定し,その関数を使用して標本がすぐに混合するかどうかを確認します。

F = fft(趋势(跟踪，“不变”）);F = F .* conj(F);ACF = ifft(F);Acf = Acf (1:21，:);%保留延迟高达20。ACF = real([ACF(1:21,1) ./ ACF(1,1)).．.Acf (1:21,2) ./ Acf (1,2)]);%正常化。边界=√(1/nsamples) * [2;2);% 95% CI为iid正常实验室= {“拦截ACF样本”，“斜坡的ACF样本”};为lineHandles = stem(0:20, ACF(:，i)，“填充”，“r-o”);lineHandles。MarkerSize = 4;网格(“上”)包含(“滞后”) ylabel(实验室{i}) hold住在图([0.5 0.5;20 20]， [bounds([1 1])) bounds([2 2])]，“- b”);Plot ([0 20]， [0 0]，“- k”);持有从A =轴;轴([1](1:3));结束

最初のラグにおける自己相関値は,拦截パラメーターにとって重要ですが,斜率パラメーターにとってはさらに重要です。相関度をさらに引き下げるため,より大きい間引きパラメーターを使用してサンプリングを繰り返すことができます。ただし，この例では現在の標本を引き続き使用します。

モデルパラメ，タ，の推定

予想どおり，標本のヒストグラムは事後密度のプロットによく似ています。

次要情节(1,1,1)hist3(跟踪,(25、25));包含(“拦截”) ylabel (“坡”) zlabel (“后验密度”)视图(-110,30)

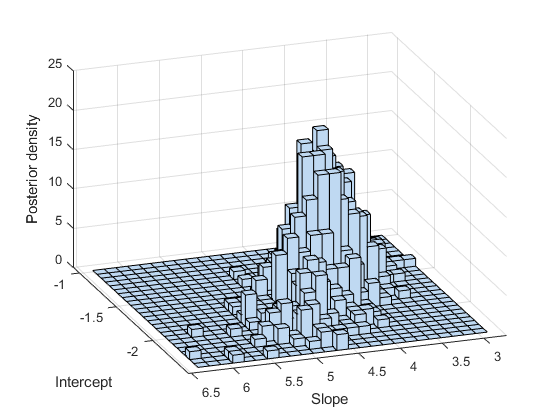
ヒストグラムまたはカーネルの平滑化密度推定を使用して,事後標本の周辺分布プロパティを集計することができます。

Subplot (2,1,1) hist(trace(:，1)) xlabel(“拦截”);Subplot (2,1,2) ksdensity(trace(:，2)) xlabel(“坡”);

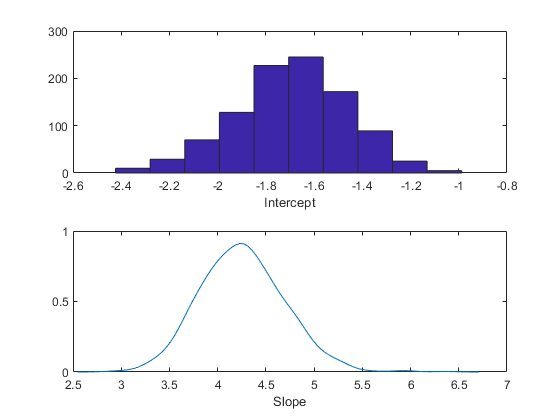
また，記述統計量(事後平均値や乱数標本の百分位など)を計算することもできます。標本サイズが目的の精度を得るのに十分な大きさかどうかを判断するには,標本数の関数としてトレースの目的の統計量を監視します。

Csum = cumsum(trace);次要情节(2,1,1)情节(csum(: 1)“。/ (1:nsamples))包含(“样本数量”) ylabel (“拦截手段”);次要情节(2,1,2)情节(csum(:, 2)’。/ (1:nsamples))包含(“样本数量”) ylabel (“斜率均值”);

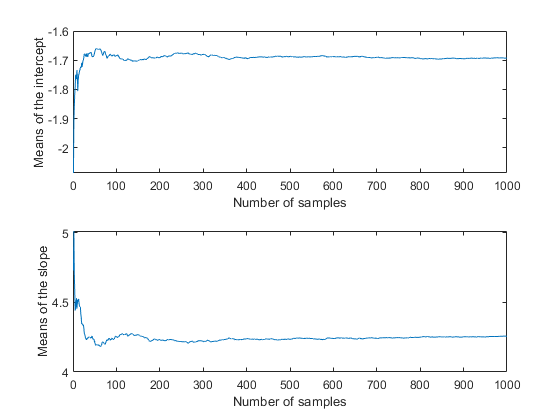
このケースでは,良好な精度の事後平均値推定を得るために,標本サイズ1000は十分すぎるほどの大きさがあるようです。

bHat = mean(trace)

bHat = -1.6931 4.2569

まとめ

统计和机器学习工具箱™には,尤度と事前分布を簡単に指定できる各種の関数が用意されています。それらの関数を組み合わせて，1の事後分布を導き出すことができます。関数slicesampleを使用すると,マルコフ連鎖モンテカルロシミュレーションを使用してMATLABでベイズ解析を実行することができます。この関数は,標準の乱数発生器を使用して標本を抽出するのが難しい事後分布に関する問題にも使用することができます。