このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。
積分
は、 は、 数学的演算 MATLAB
g=cos(在+b时)
微分とは対照的に、シンボリックな積分はより複雑な作業です。多くの難問が、積分の計算において生じ得ます。
積分 馴染みのない関数を定義する 不定積分が存在しても、ソフトウェアがそれを求められない 大型コンピューターでは不定積分の検出が可能でも、使用しているマシンではメモリと時間の不足で求められない それにもかかわらず、多くの場合、MATLABはシンボリックな積分をうまく実行できます。たとえば、次のシンボリック変数を作成します。
次の表に、これらの変数を含んだ式の積分を示します。
F int(f) 最後の例 MATLABが関数 定積分も行えます。
定積分 コマンド
ここで、別の例をいくつか示します。
F a、 b int(f,a,b) ベッセル関数 ( は以下を返します。
コマンド
は以下を返します。
シンボリック積分における困難の 1.つは、さまざまなパラメーターの "値" です。たとえば A.が任意の正の実数の場合、式
は、xが ただし、次の積分を計算しようとする場合
A.に値が与えられていない場合は、MATLABは A.を複素数であると仮定します。そのため、A.の偏角に依存する区分的解を返します。A.が正の実数の場合のみを考える場合、 次のコマンド群を使って、前述の積分を計算します。
次の値が返されます。
以下の積分
を 前のコマンドは、複素数出力を行います。
関数
高精度の数値積分が 符号数学工具箱™ の関数 詳細は、Fがシンボリック式の場合、
int(f)
=Fとなる別のシンボリック式int(f,v)
整数(x^n)または
int(sin(2*x),0,pi/2)または
g=cos(a*t+b)int(g)または
int(贝塞尔(1,z))または
符号
符号x n f=x^n;
int(f)
ans=分段(n==-1,对数(x),n=-1,。。。(n+1)/(n+1))
syms y f=y^(-1);
int(f)
ans=对数(y)
符号x n f=n^x;
int(f)
ans=n^x/日志(n)
符号a bθf=sin(a*θ+b);
int(f)
ans=-cos(b+a*θ)/a
符号u f=1/(1+u^2);
int(f)
ans=atan(u)
符号x f=exp(-x^2);
int(f)
ans=(pi^(1/2)*erf(x))/2
int(f,a,b)
int(f,v,a,b)
符号x f=x^7;
a=0;b=1;
int(f,a,b)
ans=1/8
符号x f=1/x;
a=1;b=2;
int(f,a,b)
ans=日志(2)
syms x f=对数(x)*sqrt(x);
a=0;b=1;
int(f,a,b)
ans=-4/9
符号x f=exp(-x^2);
a=0;b=inf;
int(f,a,b)
ans=pi^(1/2)/2
symszf=besselj(1,z)^2;
a=0;b=1;
int(f,a,b)
ans=超几何([3/2,3/2][2, 5/2, 3], -1)/12
贝塞尔) の例に対して、関数双重的を使って、積分値の数値近似を計算することが可能です。コマンド
符号za=int(贝塞尔(1,z)^2,0,1)
a=超几何([3/2,3/2],[2,5/2,3],-1)/12
a=双(a)
a=0.0717
実数パラメーターをもつ積分
符号
符号a假设(a>0)
符号x f=exp(-a*x^2);int(f,x,-inf,inf)
ans=pi^(1/2)/a^(1/2)
複素数パラメーターの積分
符号a x f=1/(a^2+x^2);F=int(F,x,-inf,inf)
符号を使用して、変数のすべての仮定を消去します。シンボリック変数と仮定の詳細は、F=(pi*signIm(1i/a))/a
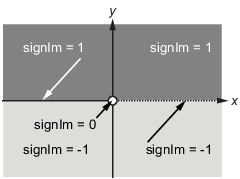
a=1+iのときのg=子系统(F,1+i)
g=pi*(1/2-1i/2)
双(g)
ans=1.5708-1.5708i
可変精度演算を使用した高精度の数値積分
vpaintegralに実装されています。完整的とは異なり、可変精度の演算を使用します。
贝塞利(5,25*u)。*exp(-u*25)を、符号u f=贝塞利(5,25*x)。*exp(-x*25);乐趣=@(u)贝塞利(5,25*u)。*exp(-u*25);usingIntegral=积分(fun,0,30)usingpaintegral=vpaintegral(f,0,30)
警告:遇到无限或非数字值。usingIntegral=NaN UsingPaintegral=0.688424
vpaintegralを参照してください。