生成拟随机数字
准随机序列
拟随机数字生成器(QRNG)产生高度均匀的单位超立方体样本。QRNG最小化差异生成点的分布与超立方体的均匀划分的每个子立方体中具有相同比例的点的分布之间。因此,qrng系统地在生成的准随机序列的任何初始片段中填充“空穴”。
与中描述的伪随机序列不同常见伪随机数生成方法,准随机序列无法通过许多随机性统计测试。然而,近似真实随机性并不是它们的目标。准随机序列寻求均匀填充空间,并以这样的方式使初始段近似此行为,直到达到指定的密度。
QRNG应用程序包括:
准蒙特卡罗(QMC)积分。蒙特卡罗技术通常用于计算困难的多维积分,而没有封闭形式的解。QMC使用准随机序列来改善这些技术的收敛性。
空间填充实验设计。在许多实验设置中,对每个因素设置进行测量是昂贵的或不可行的。拟随机序列提供了有效的、均匀的设计空间采样。
全局优化。优化算法通常在初始值附近找到局部最优值。通过使用初始值的准随机序列,搜索全局最优值,均匀地采样所有局部极小值的吸引域。
例如:使用Scramble、Leap和Skip
想象一个简单的一维序列,它产生从1到10的整数。这是基本序列,前三个点是(1、2、3):
![]()
现在看看怎么做爬,跳过,飞跃协同工作:
爬-置乱以几种不同的方式之一对点进行置乱。在本例中,假设置乱将序列转换为1,3,5,7,9,2,4,6,8,10.前三点是现在[1,3,5]: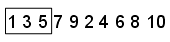
跳过——一个跳过Value指定要忽略的初始点的数量。在本例中,设置跳过值设置为2。序列现在为5、7、9、2、4、6、8、10前三点是[5,7,9]:
飞跃——一个飞跃值指定每次获取时要忽略的点数跳过设置为2,如果你设置飞跃对于1,序列使用每隔一个点。在本例中,序列现在为5、9、4、8前三点是[5 9 4]:
拟随机点集
统计和机器学习工具箱™ 函数支持这些准随机序列:金宝app
准随机序列是从正整数到单位超立方体的函数。为了在应用中有用,初始点集必须生成一个序列。点集是大小矩阵N——- - - - - -D,在那里N点数是多少D为被采样的超立方体的维数。的函数haltonset和索波尔塞特构造具有指定准随机序列特性的点集。点集的初始线段由净的方法haltonset和索波尔塞特类,但可以更普遍地使用括号索引生成和访问点。
由于准随机序列的生成方式,它们可能包含不需要的相关性,尤其是在其初始段中,尤其是在更高维度中。为了解决这个问题,准随机点集跳过,飞跃结束,或争夺序列中的值。的haltonset和索波尔塞特函数允许你指定两个跳过和飞跃拟随机序列的性质,以及争夺的方法haltonset和索波尔塞特类允许应用各种置乱技术。置乱减少了相关性,同时也提高了一致性。
生成拟随机点集
这个例子展示了如何使用haltonset构造一个二维Halton拟随机点集。
创建一个haltonset对象P,跳过序列的前1000个值,然后保留每个101点。
rng违约%的再现性p=哈尔顿组(2,“跳过”1 e3,“飞跃”1 e2)
p = Halton点设置在2维(89180190640991点)属性:跳过:1000跳过:100 ScrambleMethod:无
对象P封装指定的准随机序列的属性。点集是有限的,其长度由跳过和飞跃性质和对点集指数大小的限制。
使用争夺应用反向基数置乱。
p=扰码(p,“RR2”)
p=二维中的Halton点集(89180190640991点)属性:跳过:1000跳跃:100跳跃方法:RR2
使用净生成前500点。
X0=净(p,500);
这个等价于
X0=p(1:500,:);
点集的值X0在访问之前不会生成并存储在内存中P使用净或括号索引。
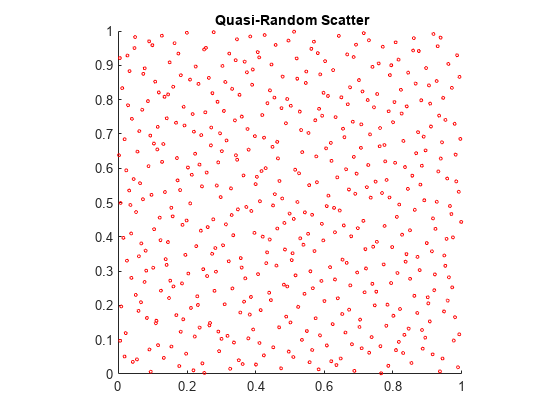
要了解准随机数的性质,请在中创建二维散点图X0.
散射(X0 (: 1), X0 (:, 2), 5,“r”)轴广场标题(“{\bf准随机散射}”)
将其与由兰德函数。
X=rand(500,2);散射(X(:,1),X(:,2),5,“b”)轴广场标题(“{\bf均匀随机散射}”)
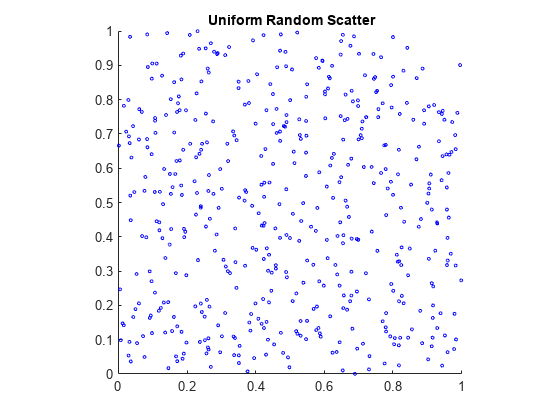
准随机散射看起来更加均匀,避免了伪随机散射中的聚集。
从统计学意义上讲,准随机数过于统一,无法通过传统的随机性测试。例如,Kolmogorov-Smirnov测试,由键糟,用于评估点集是否具有均匀的随机分布。当对均匀的伪随机样本重复执行时,例如兰德,该测试产生了均匀分布的P-价值观。
NTEST=1e5;样本大小=50;PVALS=0(NTEST,1);对于测试=1:NTESTx=rand(sampSize,1);[h,pval]=kstest(x[x,x]);PVALS(test)=pval;结束直方图(PVALS,100) h = findobj(gca,“类型”,“补丁”);xlabel(“{\ p}值”)伊拉贝尔(“测试次数”)
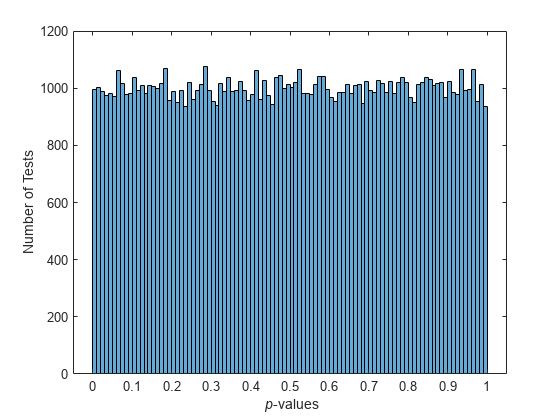
在均匀的准随机样本上反复进行试验,结果有很大的不同。
p = haltonset (1,“跳过”1 e3,“飞跃”1 e2);p=扰码(p,“RR2”); nTests=1e5;sampSize=50;PVALS=零(NTEST,1);对于测试=1:NTESTx=p(测试:测试+(sampSize-1),:);[h,pval]=kstest(x,[x,x]);PVALS(测试)=pval;结束直方图(PVALS,100)xlabel(“{\ p}值”)伊拉贝尔(“测试次数”)
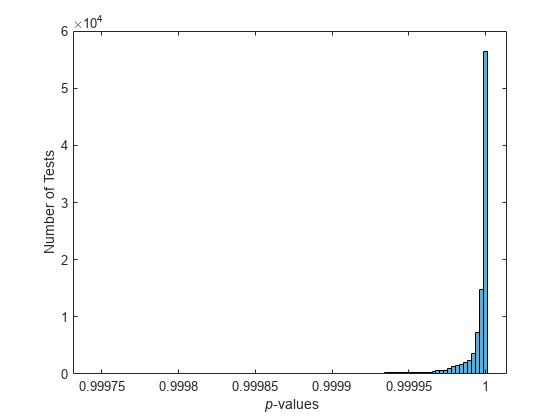
小的P-这些值对数据均匀分布的无效假设提出了质疑。如果这个假设是真的,大约5%的P-值预计将低于0.05。结果是非常一致的,他们没有挑战假设。
准随机流
准随机流,由qrandstream函数,用于生成序列的准随机输出,而不是特定大小的点集。流的使用类似于pseudoRNGS,例如兰德,当客户端应用程序需要可以间歇访问的大小不定的准随机数源时。准随机流的属性,比如它的类型(Halton或Sobol)、维度、跳过、跳跃和混乱,在构造流时设置。
在实现中,准随机流本质上是非常大的准随机点集,尽管它们的访问方式不同。的状态准随机流的标量索引是从流中取下的下一个点的标量索引。使用基兰的方法qrandstream类从流中生成点,从当前状态开始重置方法将状态重置为1.。与点集不同,流不支持括号索引。金宝app
生成一个准随机流
此示例演示如何从准随机点集生成样本。
使用haltonset创建准随机点集的步骤P,然后重复将索引增加到点集中测验生成不同的样本。
p = haltonset (1,“跳过”1 e3,“飞跃”1 e2);p=扰码(p,“RR2”); nTests=1e5;sampSize=50;PVALS=零(NTEST,1);对于测试=1:NTESTx=p(测试:测试+(sampSize-1),:);[h,pval]=kstest(x,[x,x]);PVALS(测试)=pval;结束
同样的结果通过使用qrandstream构造一个准随机流Q基于点集P并让流处理索引的增量。
p = haltonset (1,“跳过”1 e3,“飞跃”1 e2);p=扰码(p,“RR2”);q = qrandstream (p);NTEST=1e5;样本大小=50;PVALS=0(NTEST,1);对于测试=1:NTESTx=qrand(q,sampSize);[h,pval]=kstest(X[X,X]);PVALS(test)=pval;结束



