整合
int(f)
试图找到另一种象征性的表达方式, 使用符号对象 数学运算 MATLAB
G=cos(在+B)
与微分相比,符号积分是一项更复杂的任务。在计算积分时可能会出现一些困难:
反导数, 反导数可以定义一个不熟悉的函数。 反导数可能存在,但软件找不到。 该软件可以在较大的计算机上找到反导数,但在可用的计算机上时间或内存不足。 然而,在许多情况下,MATLAB可以成功地执行符号积分。例如,创建符号变量
下表说明了包含这些变量的表达式的集成。
F int(f) 在最后一个例子中, 如果MATLAB无法找到函数积分的答案 定积分也是可能的。
定积分 命令
这里有一些额外的例子。
F a、 b int(f,a,b) 关于贝塞尔函数( 回来
指挥部呢
返回
符号集成涉及的一个微妙之处是各种参数的“值”A.是任何正实数,表达式
是正的钟形曲线,当x倾向于 但是,如果您尝试计算积分
不给它赋值A.,MATLAB假设A.表示复数,因此返回取决于A.. 如果你只对这个案子感兴趣A.是一个正实数,使用 现在可以使用命令计算前面的积分
这是回报
计算积分
对于 使用 前面的命令生成复杂的输出
功能
评价 该系统实现了高精度的数值积分 整合 有关详细信息,请参阅=F.就是,int(f,v)
整数(x^n)或
int(sin(2*x),0,pi/2)或
g=cos(a*t+b)int(g)或
int(贝塞尔(1,z))或
符号
符号x n f=x^n;
int(f)
ans=分段(n==-1,log(x),n~=-1,…x^(n+1)/(n+1))
syms y f=y^(-1);
int(f)
ans=对数(y)
符号x n f=n^x;
int(f)
ans=n^x/日志(n)
符号a bθf=sin(a*θ+b);
int(f)
ans=-cos(b+a*θ)/a
符号u f=1/(1+u^2);
int(f)
ans=atan(u)
符号x f=exp(-x^2);
int(f)
ans=(pi^(1/2)*erf(x))/2
int(f,a,b)
int(f,v,a,b)
符号x f=x^7;
a=0;b=1;
int(f,a,b)
ans=1/8
符号x f=1/x;
a=1;b=2;
int(f,a,b)
ans=日志(2)
syms x f=对数(x)*sqrt(x);
a=0;b=1;
int(f,a,b)
ans=-4/9
符号x f=exp(-x^2);
a=0;b=inf;
int(f,a,b)
ans=pi^(1/2)/2
symszf=besselj(1,z)^2;
a=0;b=1;
int(f,a,b)
ans=超几何([3/2,3/2],…[2,5/2,3],-1)/12
贝塞尔)例如,可以使用双重的功能。命令
符号za=int(贝塞尔(1,z)^2,0,1)
a=超几何([3/2,3/2],[2,5/2,3],-1)/12
a=双(a)
a=0.0717
实参数积分
符号
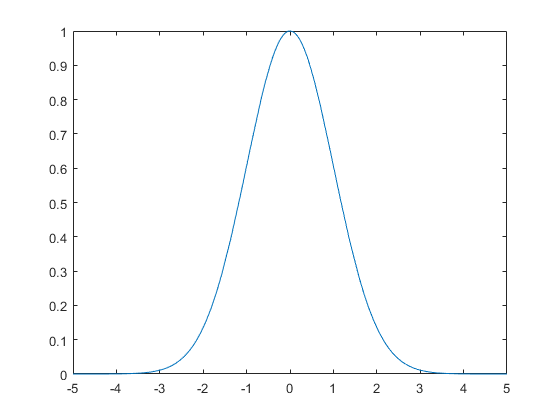
符号a假设(a>0)
符号x f=exp(-a*x^2);int(f,x,-inf,inf)
ans=pi^(1/2)/a^(1/2)
复杂参数的积分
符号a x f=1/(a^2+x^2);f=int(f,x,-inf,inf)
F=(pi*signIm(1i/a))/a

g=子系统(F,1+i)
g=pi*(1/2-1i/2)
双(g)
ans=1.5708-1.5708i
采用变精度算法的高精度数值积分
vpaintegral符号数学工具箱的功能™.完整的函数,它使用双精度算法。
符号u f=besseli(5,25*x)。*exp(-x*25);fun=@(u)besseli(5,25*u)。*exp(-u*25);usingIntegral=integral(fun,0,30)usingVpaintegral=vpaintegral(f,0,30)
警告:遇到无限或非数字值。usingIntegral=NaN UsingPaintegral=0.688424
vpaintegral.