选择样本量
这个例子展示了如何确定进行统计检验所需的样本或观察的数量。它举例说明了一个简单问题的样本量计算,然后说明了如何使用sampsizepwr函数用于计算两个更实际问题的能力和样本大小。最后,它说明了使用统计学和机器学习工具箱™函数来计算测试所需的样本大小sampsizepwr函数不支持。金宝app
用已知标准差检验正态平均数,单边
为了介绍一些概念,让我们考虑一个不现实的简单例子我们想测试均值,我们知道标准差。我们的数据是连续的,可以用正态分布来建模。我们需要确定样本容量N,以便区分平均值为100和平均值为110。我们知道标准差是20。
当我们进行统计检验时,我们通常检验a零假设针对一个替代假设。我们找到一个检验统计量T,并查看它在零假设下的分布。如果我们观察到一个异常值,比如说如果零假设为真,发生概率小于5%,那么我们会拒绝零假设,而选择另一个。(5%的概率称为显著性水平测试的)。如果值不是异常的,我们不拒绝零假设。
在这种情况下,检验统计量T是样本均值。在零假设下,均值为100,标准差为20/根号N。首先我们来看固定的样本容量,假设N=16。我们拒绝零假设如果T在阴影区域,也就是分布的上尾。这是一个片面的检验,因为我们不会拒绝T在下尾。阴影区域的截止点是均值以上1.6个标准差。
rng (0,“旋风”);mu0 = 100;sig = 20;N = 16;α= 0.05;参看= 1α;cutoff = norminv(conf, mu0, sig/sqrt(N)); / /配置文件X = [linspace(90,cutoff), linspace(cutoff,127)];y = normpdf (x, mu0团体/√(N));h1 =情节(x, y); xhi = [cutoff, x(x>=cutoff)]; yhi = [0, y(x>=cutoff)]; patch(xhi,yhi,“b”);标题('样本均值分布,N=16');包含(样本均值的);ylabel (“密度”);文本(96 .01 sprintf (“拒绝如果意味着> %。4 g \ nProb = 0.05 ',截止),“颜色”,“b”);
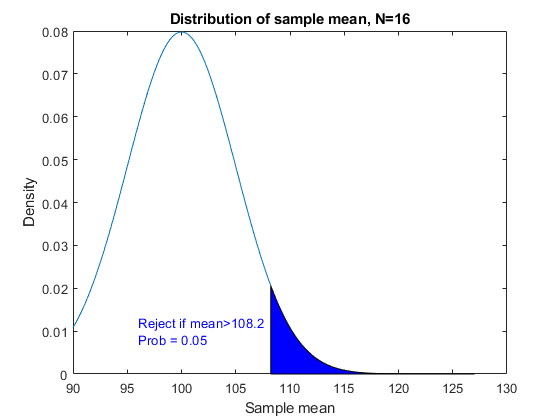
这就是T在零假设下的表现,但在另一种情况下呢?备选分布的均值是110,用红色曲线表示。
mu1 = 110;y2 = normpdf (x, mu1团体/√(N));h2 =线(x, y2,“颜色”,“r”);Yhi = [0, y2(x>=cutoff)];补丁(xhi yhi,“r”,“FaceAlpha”P=1-normcdf(截止,mu1,sig/sqrt(N));文本(115.06,sprintf('如果T>%.4g,则拒绝\n广播=%.2g',截止,P),“颜色”, (1 0 0));传奇((h1 h2),“无效假设”,备择假设的);
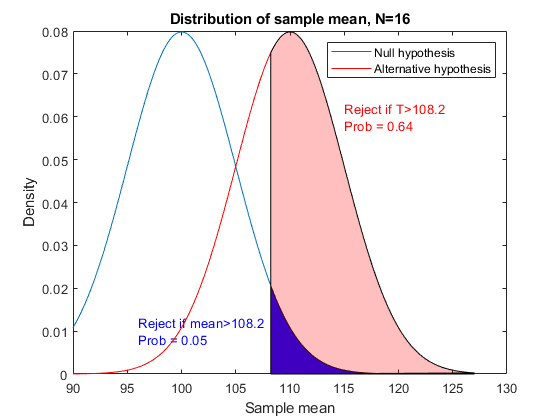
如果选择是正确的,那么拒绝无效假设的可能性更大。这正是我们想要的。如果我们看累积分布函数(cdf)而不是密度(pdf),就更容易可视化。我们可以直接从这个图中读取概率,而不必计算面积。
ynull = normcdf (x, mu0团体/√(N));yalt = normcdf (x, mu1团体/√(N));ynull h12 =情节(x,“b -”,x,yalt,的r -); zval=norminv(conf);截止值=mu0+zval*sig/sqrt(N);行([90,截止,截止],[conf,conf,0],“线型”,':');msg=sprintf('截止值= 100 + %。2g \\乘以20 / \\surd{n}', zval);文本(截止,酒精含量、味精、“颜色”,“b”); 文本(最小值(x)、配置、sprintf(“% % % g测试”,100*alpha),“颜色”,“b”,...“verticalalignment”,“高级”) palt = normcdf(cutoff,mu1,sig/根号(N));线([90,截止],[palt palt],“颜色”,“r”,“线型”,':');文本(91年,palt + .02 sprintf (“权力是1%。2 g = % .2g ',palt,1-palt),“颜色”, (1 0 0));传奇(h12“无效假设”,备择假设的);
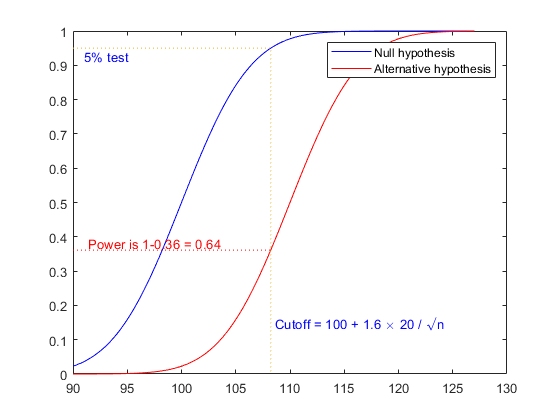
该图显示了当N=16时,两个不同mu值获得显著统计(拒绝零假设)的概率。
的幂函数定义为当备择为真时拒绝零假设的概率。它取决于备选方案的价值和样本量。我们将把幂(即1减去cdf)作为N的函数画出来,将其固定为110。我们将选择N来达到80%的乘方。从图中可以看出,我们需要N=25。
DesiredPower = 0.80;Nvec = 1:30;cutoff = mu0 + norminv(conf)*sig./sqrt(Nvec);电源= 1 - normcdf(cutoff, mu1, sig./sqrt(Nvec));情节(Nvec、电力、“博——”,[0 30],[DesiredPower DesiredPower],“k:”);包含('N =样本量') ylabel (“权力”)头衔('备用电源功能:\mu=110')

在这个过于简单的示例中,有一个公式可以直接计算所需的值,以获得80%的幂:
Mudiff = (mu1 - mu0) / sig;N80 = ceiv (((norminv(1-DesiredPower)-norminv(conf)) / mudiff)^2)
歌曲到手机上= 25
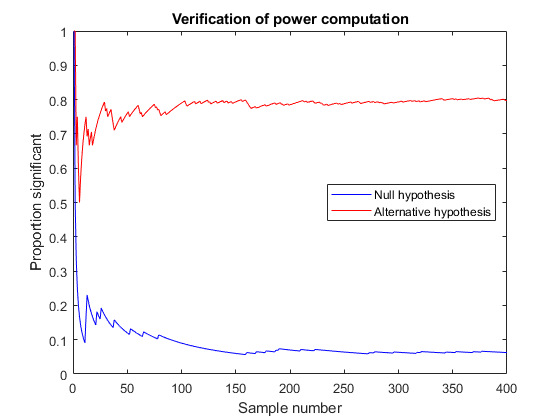
为了验证这一方法的有效性,让我们进行蒙特卡洛模拟,生成400个样本,大小为25,均在零假设(均值为100)和备择假设(均值为110)下。如果我们测试每个样本,看看其均值是否为100,我们应该预期第一组的5%和第二组的80%是显著的。
nsamples = 400;samplenum = 1: nsamples;N = 25;nsamples h0 = 0 (1);h1 = h0;为j=1:NsamplesZ0=normrnd(mu0,sig,N,1);h0(j)=ztest(Z0,mu0,sig,alpha,“对”);Z1 = normrnd (mu1,团体,N, 1);h1 (j) =中兴通讯(Z1、mu0团体,α,“对”);结束p0=cumsum(h0)。/samplenum;p1=cumsum(h1)。/samplenum;plot(samplenum,p0,“b -”samplenum p1,的r -)包含(“样本编号”) ylabel (的比例显著)头衔(“功率计算的验证”)传说(“无效假设”,备择假设的,“位置”,“东方”)
测试标准偏差未知的正态平均值,双侧
假设我们不知道标准差,我们想进行双侧检验,也就是拒绝零假设不管样本均值是高是低。
检验统计量为t统计量,即样本平均值与被测平均值之间的差值除以平均值的标准误差。在零假设下,这具有N-1个自由度的Student t分布。在另一种假设下,分布为非中心t分布,非中心参数等于真实平均值和被测平均值之间的归一化差。
对于这个双边检验,我们必须在零假设下为两个反面分配5%的错误概率,如果检验统计量在任何一个方向上都太极端,则拒绝。我们还必须考虑任意选项下的两个反面。
N = 16;df = n - 1;α= 0.05;参看= 1α;cutoff1 = tinv(α/ 2,df);cutoff2 = tinv(1α/ 2,df);X = [linspace(-5,cutoff1), linspace(cutoff1,cutoff2),linspace(cutoff2,5)];y = tpdf (x, df);h1 =情节(x, y);xlo = [x (x < = cutoff1) cutoff1]; ylo = [y(x<=cutoff1),0]; xhi = [cutoff2,x(x>=cutoff2)]; yhi = [0, y(x>=cutoff2)]; patch(xlo,ylo,“b”);补丁(xhi yhi,“b”);标题('t统计量分布,N=16');包含(“t”);ylabel (“密度”);文本(2.5,0。,sprintf (“拒绝如果t > %。4 g \ nProb = 0.025 ',截止日期2),“颜色”,“b”);文本(-4.5.05,sprintf)('如果t<%.4g\n预测值=0.025,则拒绝'cutoff1),“颜色”,“b”);

我们可以把它看成是mu的函数而不是在零假设下的幂函数。当mu在任意方向远离零假设值时,幂会增加。我们可以使用sampsizepwr命令功能,用于计算功率。对于功率计算,我们需要指定一个标准偏差的值,我们认为它大约是20。这是样本容量N=16时的幂函数图。
N=16;x=linspace(90127);power=sampsizepwr(“t”20 [100], x, [], N);情节(x,权力);包含(“真实平均值”) ylabel (“权力”)头衔(' N=16的幂函数')

均值是110时,我们需要80%的幂。根据这张图,在样本量N=16时,我们的能力小于50%。什么样的样本量才能满足我们的需求?
N = sampsizepwr (“t”20[100], 110年,0.8)
N=34
我们需要34个样本。与前面的例子相比,我们需要额外的9个观察来允许一个双边检验,以弥补不知道真实的标准偏差。
我们可以画出不同N值的幂函数图。
Nvec=2:40;功率=sampsizepwr(“t”, 110年20 [100],[],Nvec);情节(Nvec、电力、“博——”,[0 40],[DesiredPower DesiredPower],“k:”);包含('N =样本量') ylabel (“权力”)头衔('备用电源功能:\mu=110')
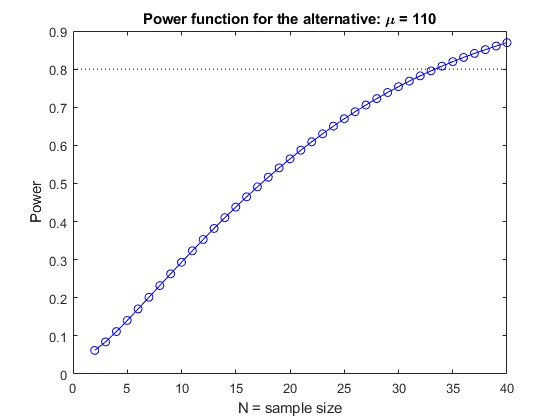
我们可以做一个类似于前一个的模拟来验证我们是否得到了所需的能量。
nsamples = 400;samplenum = 1: nsamples;N = 34;nsamples h0 = 0 (1);h1 = h0;为j = 1:nsamples Z0 = normrnd(mu0,sig,N,1);h0 (j) = tt (Z0 mu0,α);Z1 = normrnd (mu1,团体,N, 1);h1 (j) = tt (Z1、mu0α);结束p0=cumsum(h0)。/samplenum;p1=cumsum(h1)。/samplenum;plot(samplenum,p0,“b -”samplenum p1,的r -)包含(“样本编号”) ylabel (的比例显著)头衔(“功率计算的验证”)传说(“无效假设”,备择假设的,“位置”,“东方”)

假设我们能够承受50%的样本量。假设我们检测备选值mu=110的能力大于80%。如果我们将该能力保持在80%,我们可以检测到什么备选值?
mu1 = sampsizepwr (“t”20[100],[]。8,50)
mu1 = 108.0837
测试比例
现在我们来讨论区分两个比例所需的样本量。假设我们抽样的总体中有30%的人倾向于某个候选人,我们想抽样足够多的人这样我们就能把这个值和33%区分开来。
这里的想法和以前一样。在这里,我们可以使用样本计数作为我们的测试统计。此计数具有二项分布。对于任何样本量N,我们都可以计算拒绝零假设的截止值P=0.30。例如,对于N=100,如果样本计数大于按以下方式计算的截止值,我们将拒绝零假设:
N = 100;α= 0.05;p0 = 0.30;p1 = 0.33;cutoff = binoinv(1-alpha, N, p0)
截止= 38
二项分布的复杂之处在于它是离散的。超过截止值的概率不准确为5%:
1 - binocdf(截止,N, p0)
ans = 0.0340
再一次,让我们计算一个样本大小范围内的替代P=0.33的能力。我们将使用单侧(右尾)测试,因为我们只对大于30%的可选值感兴趣。
Nvec=50:50:2000;功率=sampsizepwr(“p”,p0,p1,[],Nvec,“尾巴”,“对”);情节(Nvec、电力、“博——”,[0 2000],[DesiredPower DesiredPower],“k:”);包含('N =样本量') ylabel (“权力”)头衔('备选方案的功率函数:p=0.33')
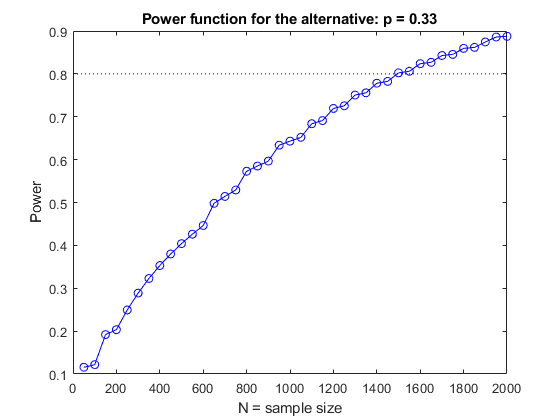
我们可以使用sampsizepwr函数要求80%的幂次所需的样本量。
approxN = sampsizepwr (“p”0.80 p0, p1, [],“尾巴”,“对”)
警告:值N>200是近似值。将功率绘制成N的函数可以显示具有所需功率的较低的N个值。approxN = 1500
一个警告信息告诉我们答案只是近似的。如果我们观察不同样本容量下的幂函数,我们会发现函数一般是递增的,但不规则因为二项分布是离散的。让我们看看在样本容量从1470到1480的范围内,p=0.30和p=0.33都拒绝零假设的概率。
子批次(3,1,1);Nvec=1470:1480;功率=sampsizepwr(“p”,p0,p1,[],Nvec,“尾巴”,“对”);情节(Nvec、电力、“ro-”[min (Nvec), max (Nvec)], [DesiredPower DesiredPower),“k:”);ylabel (sprintf (的概率(T >截止)\ nif p = 0.33 ') h_gca = gca;h_gca。XTickLabel ='';ylim([78.82]);子批次(3,1,2);alf=sampsizepwr(“p”Nvec p0, p0, [],“尾巴”,“对”);情节(Nvec,阿尔夫,“博——”[min (Nvec), max (Nvec)],[αα],“k:”);ylabel (sprintf (的概率(T >截止)\ nif p = 0.30 ') h_gca = gca;h_gca。XTickLabel ='';ylim([0.04,.06]);子批次(3,1,3);截止值=binoiv(1-alpha,Nvec,p0);绘图(Nvec,截止值,“去——”);包含('N =样本量') ylabel (“截止”)
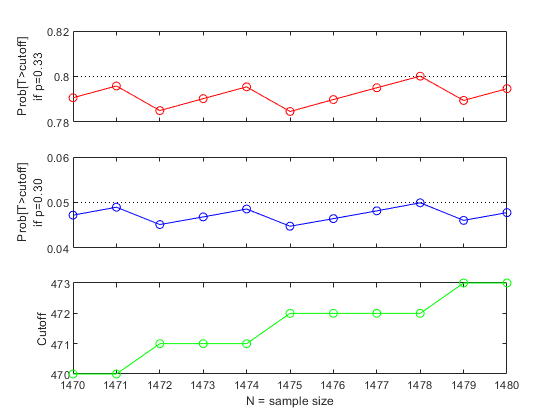
这张图揭示了幂函数曲线(上图)不仅是不规则的,而且在某些样本量下也会减小。为了使显著性水平(中间图)不大于5%,有必要增加临界值(底部图)。我们可以在这个范围内找到一个更小的样本量,提供所需的80%的功率:
最小值(Nvec(功率>=0.80))
ans = 1478
测试相关
在我们目前所考虑的例子中,我们能够计算出检验统计量达到某一显著性水平的临界值,并计算在备选假设下超过该临界值的概率。对于最后一个例子,让我们考虑一个不那么容易的问题。
假设我们可以从两个变量X和Y中抽取样本,我们想知道需要多大的样本容量来测试它们是否不相关,而另一种情况是它们的相关性高达0.4。虽然可以通过将样本相关性转换为t分布来求出样本相关性的分布,但我们可以使用一种方法,即使在无法求出检验统计量分布的问题中也可以使用这种方法。
对于给定的样本量,我们可以使用蒙特卡罗模拟来确定一个近似的截止值来检验相关性。让我们做一个大的模拟运行,这样我们可以准确地得到这个值。我们的样本量是25。
nsamples = 10000;N = 25;α= 0.05;参看= 1α;r = 0(1、nsamples);为j = 1:nsamples xy = normrnd(0,1,N,2);r (j) = corr (xy (: 1), xy (:, 2));结束截止=分位数(r, conf)
截止= 0.3372
然后我们可以在备择假设下生成样本,并估计检验的威力。
nsamples = 1000;μ= [0;0);Sig = [1 0.4;0.4 - 1];r = 0(1、nsamples);为j = 1:nsamples xy = mvnrnd(mu,sig,N);r (j) = corr (xy (: 1), xy (:, 2));结束(电力、powerci) = binofit(和(r >截止),nsamples)
Power = 0.6470 powerci = 0.6165 0.6767
我们估计幂是65%,我们有95%的信心真值在62%到68%之间。为了得到80%的幂,我们需要更大的样本量。我们可以尝试将N增加到50,估计这个样本大小的截止值,并重复功率模拟。
nsamples = 10000;N = 50;α= 0.05;参看= 1α;r = 0(1、nsamples);为j = 1:nsamples xy = normrnd(0,1,N,2);r (j) = corr (xy (: 1), xy (:, 2));结束Cutoff = quantile(r,conf) nsamples = 1000;μ= [0;0);Sig = [1 0.4;0.4 - 1];r = 0(1、nsamples);为j = 1:nsamples xy = mvnrnd(mu,sig,N);r (j) = corr (xy (: 1), xy (:, 2));结束(电力、powerci) = binofit(和(r >截止),nsamples)
Cutoff = 0.2315 power = 0.8990 powerci = 0.8786 0.9170
这个样本量比我们80%的目标更有效。我们可以继续以这种方式进行实验,试图找到一个小于50的样本量来满足我们的要求。
结论
统计和机器学习工具箱中的概率函数可用于确定在假设检验中达到所需功率水平所需的样本量。在某些问题中,样本量可直接计算;在另一些问题中,有必要搜索一系列样本量,直到找到正确的值。随机数发电机可帮助验证是否满足所需功率,也可用于研究替代条件下特定测试的功率。

