好吧，我写得太有趣了上一篇博文探索算法缩放。我想用一些“真实”的代码来探索这一点，还有什么比函数计算更真实的可爱斐波纳契数是面试问题、算法课程的宠儿我们的自己的以前的博客。这将是很有趣的探索，不仅是为了巩固我们用于探索可伸缩性的方法，而且因为看到在MATLAB中编写斐波那契函数是多么快速和优雅是很有趣的。

首先，让我们直接根据定义来看看最明显的解决方案:

函数F = fibonacci1(n)如果N < 1 f = 0;elseifN < 3 f = 1;其他的F = fibonacci1(n-1) + fibonacci1(n-2);结束结束

这是非常好的和可读的，读起来完全像斐波那契数的定义，但我们会看到不幸的是，它不是非常有效的。这是低效的，因为递归方法需要不断地重新计算$n$的较低值。

让我们创建一个参数化测试来调用这个算法。正如我提到的，这个解爆炸得很快所以我要从0到25取10个线性间隔的点。还要注意，对于较小的n，计算速度很快，因此我们需要在循环中执行此操作以获得有效的测量值。

classdefFirstFibonacciTest < matlab.perftest.TestCase属性(TestParameter) size = num2cell(round(linspace(0,25,10)));结束方法(测试)函数testFibonacci(~、大小)为Idx = 1:1000 fibonacci1(size);结束结束结束结束

它是怎么做的?

递归结果= runperf(“FirstFibonacciTest”）;findMins = @(resultArray) arrayfun(@(result) min(result. samples . measuredtime)， resultArray);Ax =轴(“XScale”，“日志”，“YScale”，“日志”）;ylabel (“执行时间(秒)”）;包含(“问题大小”）;持有在;网格在;问题大小= linspace(0,25,10);plot(ax, problemSize, findMins(recursiveResult)，“线宽”， 2) leg = legend({“递归”}）;

运行FirstFibonacciTest  .......... .......... .......... .......... .......... .......... .......... .......... .Done FirstFibonacciTest __________

$ \ mathcal {O} (2 ^ n)美元。指数。大于25的问题规模很快就会变得无效。

那么，下一个方法是什么?计算斐波那契数的一个常见解决方案是认识到我们不需要为每个$n$重新计算$n-1$和$n-2$。相反，我们可以将这些值存储到一个数组中，然后计算数字迭代。注意，这实际上是动态规划的一种简单形式，因为它在内存中保留问题的先前解决方案，并使用这些先前的解决方案来计算后续的值。金宝搏官方网站从本质上讲，我们获得了相当可观的效率提升，因为我们利用了内存的优势。这看起来怎么样?我们可以将第n个$ fibonacci数与$n+1$和$n+2$的fibonacci数一起存储在一个三元素数组中，并迭代地处理每个fibonacci数，不断更新我们的3元素向量。

函数F = fibonacci2(n) values = [0 1 1];为Q = 1:n个值(1:2)=值(2:3);Values (3) = sum(Values (1:2));结束F = values(1);结束

为了观察它是如何扩展的，我将修改我们的测试，将算法作为另一个测试参数传递进来，这样我们就可以重用我们已经编写的测试，并确保测量的一致性。我们不希望一种算法使用1000个循环来测量，而另一种算法意外地使用2000个循环来测量。

在不同的fibonacci实现中添加了包含函数句柄的算法测试参数，测试看起来是一样的。

classdefSecondFibonacciTest < matlab.perftest.TestCase属性(TestParameter)算法= struct…“递归”@fibonacci1,…“迭代”, @fibonacci2);Size = num2cell(round(linspace(0,25,10)));结束方法(测试)函数testFibonacci(~，算法，大小)为Idx = 1:1000算法(大小);结束结束结束结束

注意，我使用了结构语法来定义参数，这允许我们给每个参数值起一个好听的名字，比如“递归”和“迭代”。这也允许我们只选择这些参数并运行感兴趣的确切子集，在这种情况下，迭代算法。

迭代结果= runperf(“SecondFibonacciTest”，“ParameterName”，“迭代”）;plot(ax, problemSize, findMins(iterativeResult)，“线宽”， 2)腿=传说;字符串,“迭代”]);

运行SecondFibonacciTest  .......... .......... .......... .......... .......... .......... .......... .......... ...Done SecondFibonacciTest __________

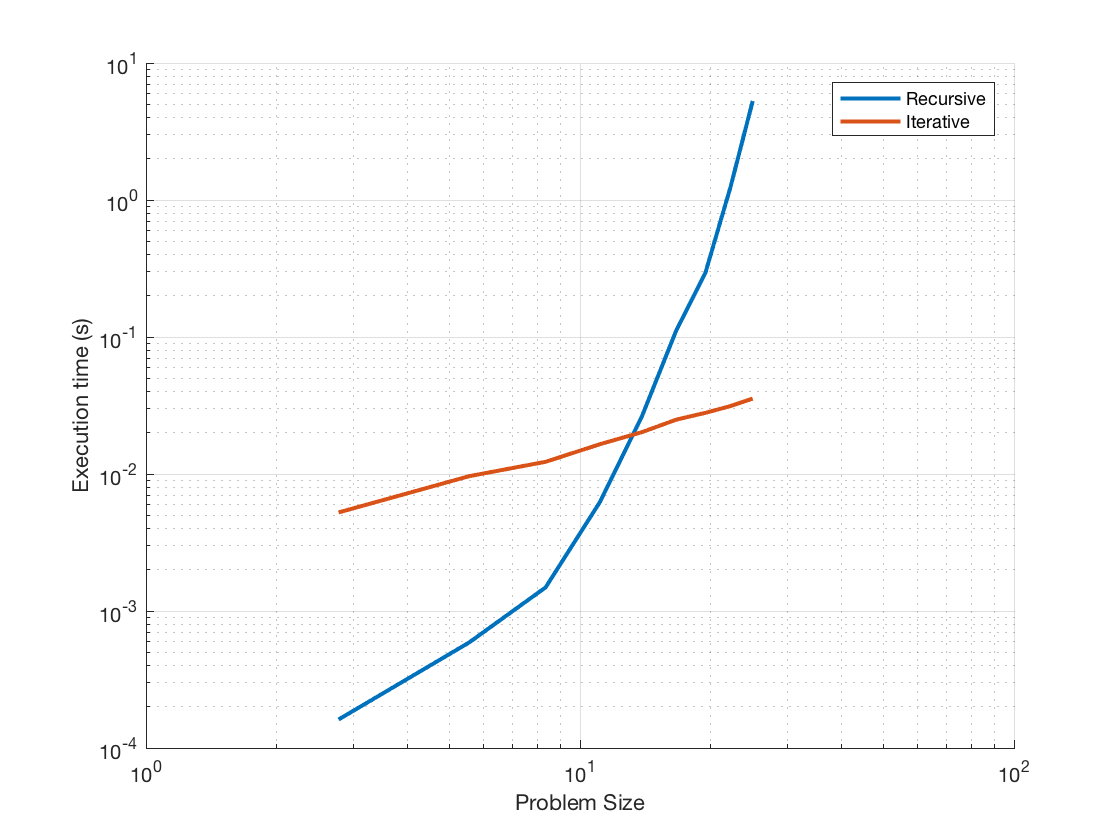
好了，我们现在看到迭代方法是线性缩放的($\mathcal{O}(n)$))，这让我们看起来更好，但实际上我们可以用封闭形式的解决方案来做得更好比奈的公式：

$ $ fn = \压裂{(1 + \ sqrt {5}) ^ n - (1 - \ sqrt {5}) ^ n} {2 ^ n \√{5}}$ $

下面是我们用MATLAB编写的代码:

函数F = fibonacci3(n) sqrt5 = sqrt(5);Num = (1 + sqrt5) n - (1 - sqrt5) n;Denom = (2^n)*sqrt5;F = num/denom;结束

…现在我们可以简单地将这个新算法作为新参数添加到我们现有的测试中:

属性(TestParameter) size = num2cell(round(linspace(0,25,10)));算法= struct(…“递归”@fibonacci1,…“迭代”@fibonacci2,…“ClosedForm”, @fibonacci3);结束

快跑!

closedFormResult = runperf(“FibonacciTest”，“ParameterName”，“ClosedForm”）;plot(ax, problemSize, findMins(closedFormResult)，“线宽”， 2)腿=传说;字符串,“闭型”]);

运行FibonacciTest  .......... .......... .......... .......... .......... .......... .......... .......... .Done FibonacciTest __________

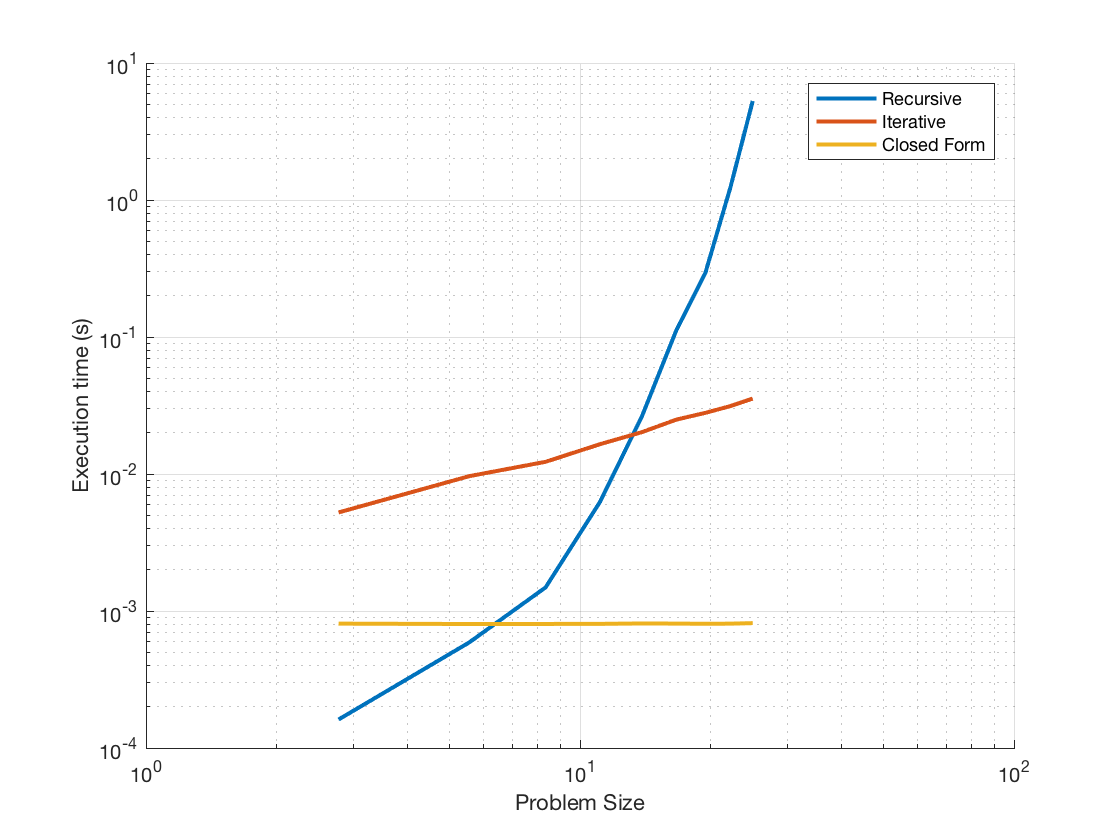
看起来很不错!事实上，它演示了$\mathcal{O}(1)$ constant行为。从复杂性的角度来看，没有比这更好的了。然而，还有一个解决方案，我想用矩阵指数来展示。嗯，我好像听说过MATLAB很擅长处理矩阵。这听起来熟悉吗?我们很幸运，因为用MATLAB的能力解起来很简单。这是因为第n个$ fibonacci数$f_n$由以下公式控制:

左$ $ \[开始\{数组}{cc} 1 & 1 \ \ 1 & 0 \结束数组{}\右)^ n = \离开[\{数组}开始f {n + 1} {cc} & fn \ \ fn & f {n}{数组}\ \端)$ $

是的，就是这样，MATLAB中的解就是这么简单。

函数f = fibonacci4(n) f = [1 1;1 0]^n;f = f (1,2);结束

这个比例是怎样的呢?添加测试并运行它。

属性(TestParameter) size = num2cell(round(linspace(0,25,10)));算法= struct(…“递归”@fibonacci1,…“迭代”@fibonacci2,…“ClosedForm”@fibonacci3,…“MatrixExponential”, @fibonacci4);结束

matrixResult = runperf(“FibonacciTest”，“ParameterName”，“MatrixExponential”）;plot(ax, problemSize, findMins(matrixResult)，“线宽”， 2)腿=传说;字符串,矩阵指数的]);

运行FibonacciTest  .......... .......... .......... .......... .......... .......... .......... .......... .......... ..........Done FibonacciTest __________

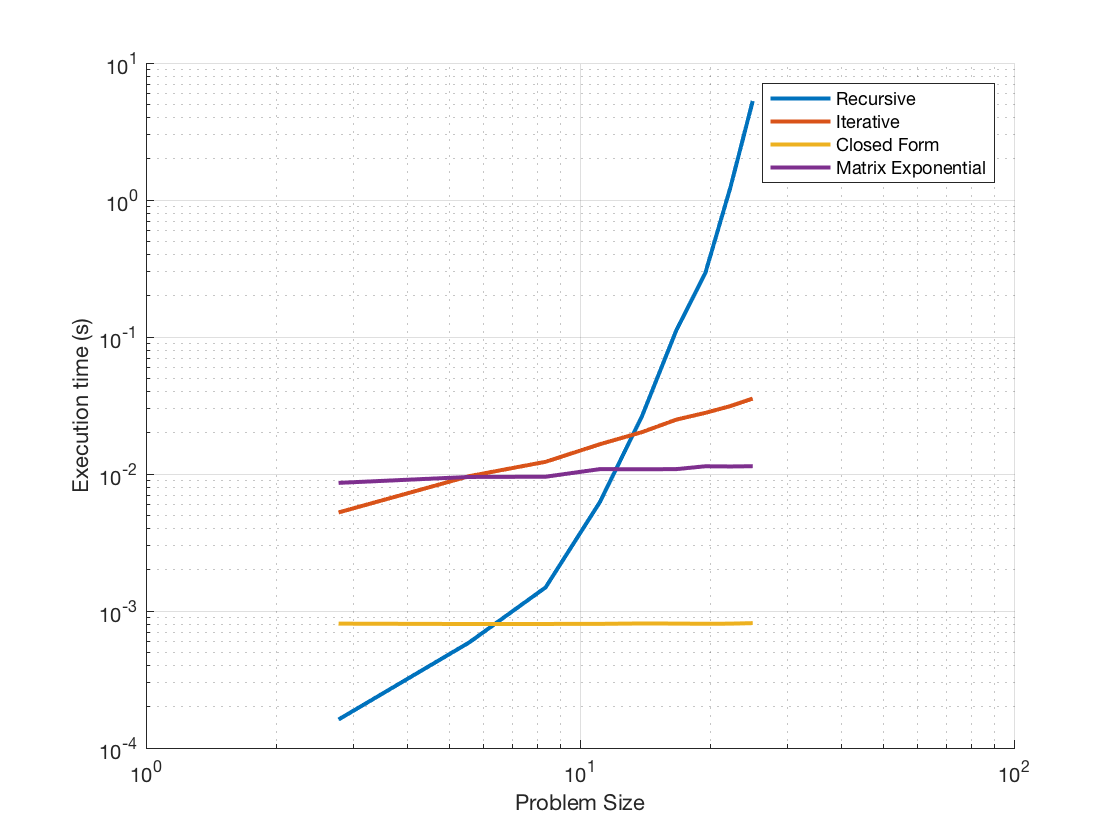
快看!封闭形式和矩阵解都显示出非常可伸缩的行为，但矩阵形式不太好，显金宝搏官方网站示对数($\mathcal{O}(\log n)$)缩放而不是常数，常数因子对于矩阵情况更大。然而，矩阵指数解还有另一个好处，而不是封闭形式的解。为了证明这一点，我将在这个测试中添加一个快速抽查，以确认我们实际上得到了正确的答案。注意，在这篇文章中，我将添加另一个测试方法来验证单个尺寸，但如果需要，这可以在现有的测试方法中对所有尺寸进行验证。

classdefVerifiedFibonacciTest < matlab.perftest.TestCase属性(TestParameter) size = num2cell(round(linspace(0,25,10)));算法= struct(…“递归”@fibonacci1,…“迭代”@fibonacci2,…“ClosedForm”@fibonacci3,…“MatrixExponential”, @fibonacci4);结束方法(测试)函数testFibonacci(~，算法，大小)为Idx = 1:1000算法(大小);结束结束函数testCase. verifyequal(算法(16)，987，…第16个斐波那契数应该是987）;结束结束结束

让我们运行它runtests确认正确性。

结果=运行测试(“VerifiedFibonacciTest”）

运行VerifiedFibonacciTest  .......... .......... .......... .......... ..================================================================================ 验证失败VerifiedFibonacciTest / testCorrectAnswer(算法= ClosedForm)。---------------- 测试诊断 : ---------------- 16斐波纳契数应该是987  --------------------- 框架的诊断 : --------------------- verifyEqual失败了。——>使用"isequal "两个值不相等。——>失败表:实际RelativeError预期错误  ______ ________ ____________________ ____________________ 987 987 4.54747350886464 4.60736930989325 e-13 e-16实际双:9.870000000000005 e + 02预期两倍:987  ------------------ 堆栈信息 : ------------------ 在/ mathworks / /文件/ dev /工具/ tia / mdd / performanceScaling / VerifiedFibonacciTest。在21米(VerifiedFibonacciTest.testCorrectAnswer)  ================================================================================ ..完成VerifiedFibonacciTest  __________ 失败失败总结:名字不完整的原因(s ) ============================================================================================================ VerifiedFibonacciTest / testCorrectAnswer(算法= ClosedForm) X验证失败。TestResult = 1x44带有属性的TestResult数组:Name Passed Failed Incomplete Duration Details总计:43 Passed, 1 Failed, 0 Incomplete. 7.3549秒测试时间。

…这是封闭形式解的问题。它受到浮点精度误差的影响。当然，我们可以通过利用verifyEqual中的容差来简单地通过这个测试

987年testCase.verifyEqual(算法(16),“RelTol”1 e-14…第16个斐波那契数应该是987）;

但事实是，使用封闭形式的解决方案，我们计算的东西接近第n $斐波那契数，但矩阵解决方案准确地计算它。使用哪一个取决于您的应用程序，但考虑到常数因子如此之小，而对数行为对于大问题规模接近常数，我想我会倾向于选择精确的解决方案。你呢?

获取MATLAB代码

发布与MATLAB®R2016a