I have recently handled several help requests for solving differential equations in MATLAB. All of the cases I worked on boil down to how to transform the higher-order equation(s) given to a system of first order equations. In this post I will outline how to accomplish this task and solve the equations in question. What I amnotgoing to talk about is details of ODE solving algorithms (maybe another time).

Contents

Simple System

Let's start with a simple, linear, second order system, a mass-spring system with motion constrained to one-dimension, a horizontal one (and therefore no gravity). Ifis the mass andis the spring constant, the equations of motion for the system are:

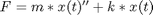
Conditions, Initial and Otherwise

To solve this system, we need to know,,, and initial conditions, e.g.,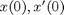(also known as position and velocity). Let's simplify things and set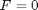, i.e., no external forces. Let's also set some initial conditions,, in other words, start with the spring unstretched and the mass moving. I end up with this system:

Transform Equation

Looking in the help, I need to set up an system of equations to enable me to use one of thenumerical ODE solversin MATLAB.

To start the transformation, let me define a new variable that I will substitute in the system.

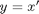
I can derive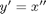

and now rewrite my ODE system in terms of.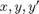

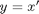
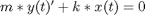
with initial conditions as above.

Now let me reorganize these 2 equations in a vector/matrix equation where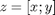

I now write me equation solely in terms of, the new vector (consisting of position and velocity). With that in mind, I will reorganize the existing equations first so I have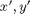on the left-hand sides.

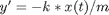
or, in terms of,

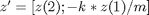
Try It!

Let's try it. Set values formandk

m = 1; k = 10;

I can create the ODE code in a file, or I can set up the equations as an anonymous function which is what I'll do here.

springmass = @(t,z)[z(2); -k * z(1)/ m];

Set up the initial conditions.

ic = [0; 1];

Solve between.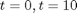

tspan = [0 10];

Call an ODE solver and plot the results.

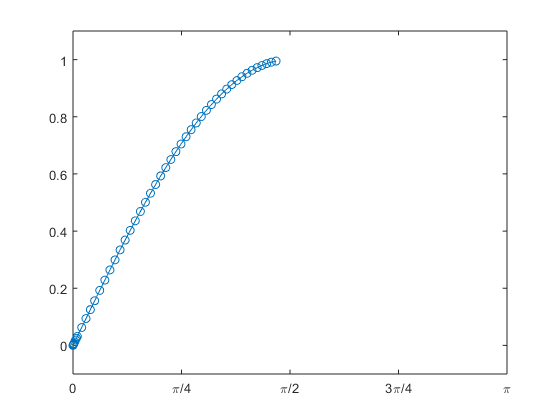
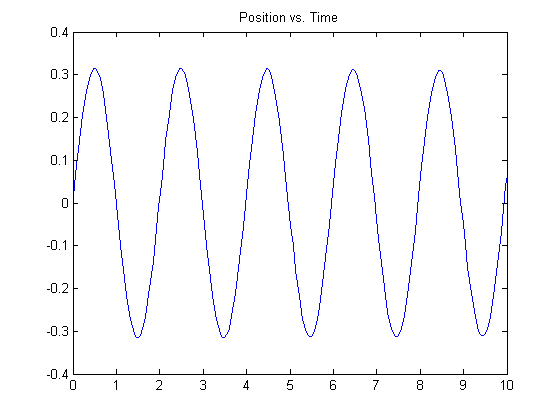
[t,y] = ode23(springmass, tspan, ic); plot(t,y(:,1)), title('Position vs. Time')

And the velocity.

plot(t,y(:,2)), title('Velocity vs. Time')

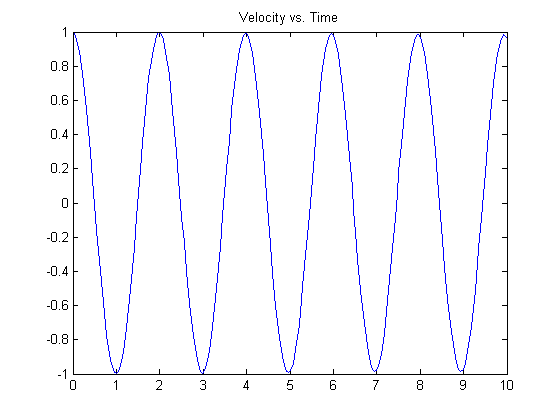
You can see the left-most points on the plots match the initial conditions specified.

Transforming Equations

Do you need to recast problems to fit into a particular formulation such as for solving ODEs? Let's hear about themhere.

Get the MATLAB code

Published with MATLAB® 7.10