Simplifying Symbolic Results
I am pleased to introduce guest blogger Kai Gehrs. Kai is a developer for theSymbolic Math Toolbox。His main focus in this post is on special approaches to symbolic simplification and equation solving.
Contents
Have You Noticed Results Not Being Simplified Well?
When using the Symbolic Math Toolbox for symbolic simplification, have you ever been wondering why it does not apply certain classic book rules automatically to return the results you have in mind?
Some of these classic book rules are:
Just usingsimplifyto get the result on input
on input does not work:
does not work:
symsabsimplify(log(a)+log(b))
ans = log(a) + log(b)
Using Assumptions on Variables
Of course, we all know that the rule applies only under appropriate mathematical assumptions on
applies only under appropriate mathematical assumptions on and
and 。For example, if we assume that
。For example, if we assume that and
and are positive, we will get the desired result:
are positive, we will get the desired result:
symsabpositivesimplify(log(a)+log(b))
ans = log(a*b)
To get rid of all previously specified assumptions, use
symsabclear
When Things Get More Complicated
Does it mean that setting the right assumptions is a universal solution here? Well, not always!
Assume and
and appear as intermediate results in some really huge symbolic computations somewhere in, lets say, line 454 of your MATLAB script. From the context of your application, you know that
appear as intermediate results in some really huge symbolic computations somewhere in, lets say, line 454 of your MATLAB script. From the context of your application, you know that and
and are positive. Now you want MATLAB to automatically compute a simplified form of
are positive. Now you want MATLAB to automatically compute a simplified form of in line 455. How will you manage to set the right assumptions?
in line 455. How will you manage to set the right assumptions?
As an example, think of and
and as being something like
as being something like
symsxya = -(x + 1)^(1/2)/((exp(x - y) - sin(x + y)) *。..(log((x^2 + 1)/(y^2 + 1))/exp(y) + (x - y)^y +。..1/(x - y)^x)); b = (cos(x)*sin(y))/((x - y)^x*(x + 1)^(1/2)) -。..(exp(x)*(x - y)^y)/(exp(y)*(x + 1)^(1/2)) +。..(cos(y)*sin(x))/((x - y)^x*(x + 1)^(1/2)) -。..(exp(x)*log((x^2 + 1)/(y^2 + 1)))/。..(exp(2*y)*(x + 1)^(1/2)) - exp(x)/。..(exp(y)*(x - y)^x*(x + 1)^(1/2)) +。..(cos(x)*sin(y)*(x - y)^y)/(x + 1)^(1/2) +。..(cos(y)*sin(x)*(x - y)^y)/(x + 1)^(1/2) +。..(log((x^2 + 1)/(y^2 + 1))*cos(x)*sin(y))/。..(exp(y)*(x + 1)^(1/2)) + (log((x^2 + 1)/。..(y^2 + 1))*cos(y)*sin(x))/(exp(y)*(x + 1)^(1/2));
Now executing thesimplifycommand does not seem to be helpful:
S = simplify(log(a)+log(b)); pretty(S)
/ y | sin(x + y) sin(x + y) (x - y) log| ------------------- + ------------------- + | x 1/2 1/2 \ (x - y) (x + 1) (x + 1) y #1 sin(x + y) exp(x) (x - y) ------------- - --------------- - #2 #2 \ exp(x) #1 exp(x) | ------------------- - -------------------------- | + 1/2 x 1/2 | exp(2 y) (x + 1) exp(y) (x - y) (x + 1) / / 1/2 / log| - ((x + 1) ) / | (exp(x - y) - sin(x + y)) | | \ \ / #1 y 1 \ \ \ | ------ + (x - y) + -------- | | | | exp(y) x | | | \ (x - y) / / / where / 2 \ | x + 1 | #1 = log| ------ | | 2 | \ y + 1 / 1/2 #2 = exp(y) (x + 1)
假设 and
and to be positive does not significantly improve the result either. The reason is that we need to set such assumptions on
to be positive does not significantly improve the result either. The reason is that we need to set such assumptions on and
and that would make the expressions
that would make the expressions and
and positive. We can try to find the right assumptions for this example, but in general it seems like one has to be a genius to guess what's appropriate.
positive. We can try to find the right assumptions for this example, but in general it seems like one has to be a genius to guess what's appropriate.
Using Option IgnoreAnalyticConstraints for Simplification
A possible solution to the problem is to ignore certain analytic constraints, that is, to use theIgnoreAnalyticConstraintsoption forsimplify。
With this option the simplifier internally applies the following rules:
 for all values of
for all values of and
and 。In particular
。In particular for all values of
for all values of ,
, and
and 。
。 for all values of
for all values of and
and 。In particular
。In particular for all values of
for all values of ,
, and
and 。
。- If
 and
and are standard math functions and
are standard math functions and holds for all small positive numbers, then
holds for all small positive numbers, then is assumed to be valid for all
is assumed to be valid for all (for example as in case of
(for example as in case of ).
).
所以how does this work in our example?
simplify(log(a)+log(b),'IgnoreAnalyticConstraints',true)
ans = 0
The result is , because
, because 。Hence, under the above assumptions, we get
。Hence, under the above assumptions, we get 。
。
Of course, it is important to keep in mind that the rules applied byIgnoreAnalyticConstraintsare not correct in a strict mathematical sense. Nevertheless, in practice these rules are often very helpful to get simpler results. Another nice side effect is that ignoring some analytic constraints often helps you speed up your computations.
Thisdocumentationdescribes more details onIgnoreAnalyticConstraints。
Using IgnoreAnalyticConstraints for Equation Solving
Not surprisingly the concept of ignoring analytic constraints also makes sense for equation solving. Imagine that you want to solve the equation for
for 。Ignoring analytic constraints would certainly mean to write this as
。Ignoring analytic constraints would certainly mean to write this as 。假设
。假设 to be nonzero we get
to be nonzero we get and, finally,
and, finally, 。
。
Without using any restrictions, Symbolic Math Toolbox returns the result:
symsxnsolve(log(x^n),x)
Warning: The solutions are parametrized by the symbols: k = Z_ intersect Dom::Interval([-1/(2*Re(1/n))], 1/(2*Re(1/n))) ans = 1/exp((pi*k*2*i)/n)
So you get a parameterized solution which strongly depends on the values of 。This is reasonable, because, for example, for
。This is reasonable, because, for example, for you get the four solutions
you get the four solutions
solve(log(x^4),x)
ans = 1 -1 i -i
whereas for there only is one solution:
there only is one solution:
solve(log(x^(1/2)),x)
ans = 1
ApplyingIgnoreAnalyticConstraintswe get
solve(log(x^n),x,'IgnoreAnalyticConstraints',true)
ans = 1
Also for equations involving roots where no additional symbolic parameters are present, it may be useful to applyIgnoreAnalyticConstraintsto get simpler results:
solve(x^(5/2) - 8^(sym(10/3)),'IgnoreAnalyticConstraints', true)
ans = 16
Here the solver ignores branch cuts during internal simplifications and, hence, returns only one solution.
See the MATLAB doc page onsolvefor further details.
TheIgnoreAnalyticConstraintsoption can also be used for other Symbolic Math Toolbox functions like the functionintfor doing symbolic integration. The option is also available for the related MuPAD Notebook Interface functions.
Have You Tried IgnoreAnalyticConstraints?
Have you tried theIgnoreAnalyticConstraintsoption to get simpler, shorter, and easier to handle results?
Let me knowhere。
- Category:
- Symbolic














 Cleve’s Corner: Cleve Moler on Mathematics and Computing
Cleve’s Corner: Cleve Moler on Mathematics and Computing The MATLAB Blog
The MATLAB Blog Steve on Image Processing with MATLAB
Steve on Image Processing with MATLAB Guy on Simulink
Guy on Simulink Deep Learning
Deep Learning Developer Zone
Developer Zone Stuart’s MATLAB Videos
Stuart’s MATLAB Videos Behind the Headlines
Behind the Headlines File Exchange Pick of the Week
File Exchange Pick of the Week Hans on IoT
Hans on IoT Student Lounge
Student Lounge MATLAB Community
MATLAB Community MATLAB ユーザーコミュニティー
MATLAB ユーザーコミュニティー Startups, Accelerators, & Entrepreneurs
Startups, Accelerators, & Entrepreneurs
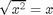


 for all values of
for all values of 。
。 for all values of
for all values of for all values of
for all values of and
and are standard math functions and
are standard math functions and holds for all small positive numbers, then
holds for all small positive numbers, then