低摆，甜蜜概率:猜测2015年橄榄球世界杯每场比赛的结果

今天的客座博主是Matt Tearle，他在MathWorks这里为我们的MATLAB培训材料工作。马特来自新西兰，他很高兴全黑队最近在2015年橄榄球世界杯上的胜利．还有什么比用MATLAB分析结果更好的庆祝方式呢?

内容

短暂的竞争

新西兰选项卡(博彩机构)为能够正确预测2015年橄榄球世界杯所有48场比赛结果的人提供了100万美元的奖金。近4.8万人参加了这场免费比赛。然而，只有79人正确选择了日本34-32爆冷南非。仅仅六场比赛之后，每一个选手出局了!

随机猜测是最好的策略吗?即使一切按计划进行，奖金又有多安全?随机抽取48个匹配结果的概率是多少?

赢或输:一个简单的分析

如果比赛只是在每场比赛中从两支队伍中选出胜者，那么猜测就相当于掷48次硬币。的概率k成功从n每次试验都有概率p由二项分布给出:

$ $ B (k) = \离开(\ n开始{数组}{c} \ \ k \结束数组{}\右)p ^ k (1 - p) ^ {n - k} $ $

这可以手动计算:

B48 = nchoosek(48,48) * 0.5^48 * (1 - 0.5)^0

B48 = 3.5527e-15

或者用binopdf统计和机器学习工具箱中的函数:

B48 = binopdf(48,48,0.5)

B48 = 3.5527e-15

漂亮的不可能!如果48000名参与者都是随机猜的，那么中奖的几率是

Anywin = 1 - binopdf(0,48000,b48)

Anywin = 1.7053e-10

也就是说，账单必须支付100万美元的几率不到十亿分之一。庄家永远赢!

让我们考虑一下一系列成功的可能性:

K = 0:48;B = binopdf(k,48,0.5);Bar (k,b) xlim([-1 49]) xlabel(“正确猜测结果的数目”) ylabel (“概率”）

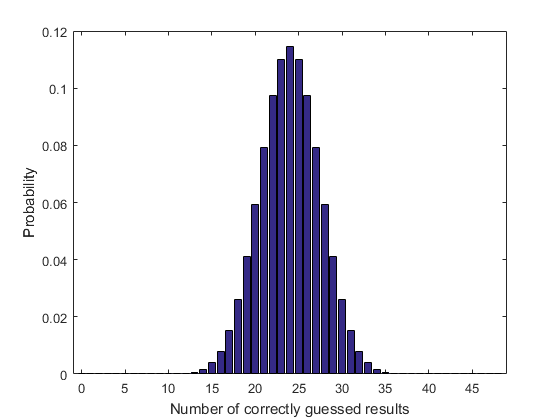
不足为奇的是，最有可能的结果是猜测结果的一半。可视化实现目标的机会也能提供信息至少正确数:给定数目的正确结果累积二项分布给出的概率k成功或更少．得到的概率最少k成功，我们需要手动积累:

栏(k, cumsum (b,“反向”)) xlim([-1 49]) ylim([0 1])网格在包含(“正确猜测结果的最少数量”) ylabel (“概率”）

高于35/48的概率非常小。

赢，输，或平局:一个更现实的方法

但更糟糕的是，游戏并没有那么简单。首先，在小组赛阶段，平局是可能的结果。此外，参赛者不仅需要猜测获胜队伍，还需要从“1-12分”或“13分或以上”两种可能性中猜测获胜的差距。总的来说，每场比赛有五种可能的选择(A队比13+，A队比1-12，平局，B队比1-12,B队比13+)。

尽管这似乎使事情变得相当复杂，但确定正确猜测给定数量结果的概率仍然是一个二项问题:一次成功的试验只是一个正确的预测。如果一切都相等，那么每次成功试验的概率是1/5而不是1/2。(最后8场淘汰赛的分析有点复杂，因为它们不是独立的，而且不允许平局。让我们把事情简单化，忽略那些细节。)

B = binopdf(k,48,0.2);Subplot (1,2,1) bar(k,b) xlim([-1 49]) xlabel({“数量”，“正确猜测的结果”}) ylabel (“概率”）%累积概率次要情节(1、2、2)栏(k, cumsum (b,“反向”)) xlim([-1 49]) ylim([0 1])网格在包含({“最小数量”，“正确猜测的结果”}) ylabel (“概率”）

奖金现在看起来更安全了!即使是20个正确的预测也不太可能。靠猜测获胜的概率低得可笑:

b(结束)

Ans = 2.8147e-34

所有事物都是不平等的:建立一个策略

但还是有一些希望的:这五项结果都是有希望的不同样可能。平局是罕见的事件。世界杯足球赛经常会出现误判(比如日本队对南非队——好吧，这是个糟糕的例子!)，这导致了巨大的胜利差距。因此，一个好的策略可能是猜测与典型结果分布相同的结果。

听起来是个好计划，但首先我们需要一些实际数据。方便,互联网的存在．使用选好就走的方便界面，我们可以查阅世界杯所有比赛的结果从1987年第一届世界杯到2015年RWC结束。结果存储在电子表格中WCresults.xlsx．

Wcdata =可读数据(“WCresults.xlsx”）;Wcdata = Wcdata (:，{“日期”，“分数”})；

警告:变量名已被修改为有效的MATLAB标识符。

分数被记录为字符串(“x - y”,在那里x而且y是每个队的分数)。我们需要把它变成一个结果。一种方法是使用正则表达式进行提取x而且y,使用str2double将它们转换为数字，然后计算结果。但这个结果将被计算为x-y．如果有一种方法可以直接将字符串解释为计算…但是，等等，有!的str2num函数实际上使用了eval将字符串解释为数值表达式(而不仅仅是数字)。然而,str2num适用于单个字符串，而不是字符串的单元格数组，所以我们需要使用cellfun也

wcdata。保证金= cellfun(@str2num,wcdata.Score);

这将添加一个新变量保证金到我们那桌去。现在我们需要bin保证金进入比赛要求的五个类别。这很容易用离散化R2015a中引入的函数。它甚至可以返回结果为分类变量。

Wincats = {“走13 +”，“客场1 - 12”，“画”，家1 - 12的，家13 + '};wcdata。结果=离散化(wcdata。保证金，[-Inf,-13,0,1,13,Inf],.．.“分类”, wincats);

现在我们需要将数据分成2015年之前的历史结果和用于测试我们的策略的2015年结果。我们可以把日期转换成adatetime变量，这使得逻辑变得简单。

wcdata。日期=日期时间(wcdata. Date =日期时间。目前为止,“InputFormat”，'eee, dd MM yyyy'）;Pre2015 = wcdata。Date < datetime(2015,1,1);Previous = wcdata(pre2015，:);Current = wcdata(~pre2015，:);

让我们来看看过去的结果是如何分布的:

次要情节(1 1 1)直方图(之前。结果,“归一化”，“pdf”）

果然，很少有平局，很多都是爆发式的。但有趣的是，这种分布并不对称。在世界杯上，除了主队，没有主队和客场之分，为什么会出现如此悬殊的情况呢?每场比赛的球队以特定的顺序列出(第一个被指定为“主队”)。显然，这个顺序不是完全随机的，因为有一个强烈的偏向于大的主场胜利。无论理由是什么，只要2015年世界杯的使用方式与前几届一样，这就无关紧要了。

假设根据这个分布猜结果的策略，猜对的概率是多少?如果我们能确定单个匹配的概率，那么剩下的就是另一个二项分布。虽然按照历史分布有直观的意义，但它可能有助于考虑如果我们猜测任何给定的分布会发生什么。

为了简单起见，让我们考虑抛硬币，75%的概率是正面朝上。假设我们选择随机猜，猜正面的概率是2/3。然后我们猜对这2/3次中的3/4次，猜错这2/3次中的1/4次。我们猜对反面的1/3次中的1/4次，猜错1/3次中的3/4次。总的来说,

dist_history = [3/4 1/4];Dist_guess = [2/3 /3];格式老鼠Allpossibilities = (dist_history ')*dist_guess

所有可能性= 1/2 1/4 1/6 1/12

总的来说，我们正确的1/2(猜测正面，是正面)+ 1/12(猜测反面，是反面)= 7/12，错误的1/6(猜测正面，是反面)+ 1/4(猜测反面，是正面)= 5/12。注意，总正确比例为

Totalright = sum(diag(所有可能性))

Totalright = 7/12

或者,同样,

Totalright = dist_historic*(dist_guess')

Totalright = 7/12

扩展到多种可能性，全部结果集就是外积。成功的概率是对角元素的和，相当于内积。

现在我们求实际的历史分布值。

格式短Dist_historic = histcounts(先前的。结果,“归一化”，“pdf”）

Dist_historic = 0.0605 0.1601 0.0107 0.1708 0.5979

如果我们用相同的分布进行猜测，那么我们在每个匹配预测中成功的概率是

Dist_guess = dist_historic;P = dist_historical *(dist_guess')

P = 0.4160

或者,同样,

P = sum(dist_history .^2)

P = 0.4160

所以这比抛硬币稍微糟糕一点。等等，最后一个元素dist_historic是0.6，所以我们应该能得到一个更高的值p只要把重点放在这一点上:

Dist_guess = [0 0 0 0.2 0.8];P = dist_history *(dist_guess') dist_guess = [0 0 0 0 1];P = dist_historical *(dist_guess')

P = 0.5125 P = 0.5979

这两个都是轻微的更好的比抛硬币还难。

B = binopdf(k,48,p);Subplot (1,2,1) bar(k,b) xlim([-1 49]) xlabel({“数量”，“正确猜测的结果”}) ylabel (“概率”）%累积概率次要情节(1、2、2)栏(k, cumsum (b,“反向”)) xlim([-1 49]) ylim([0 1])网格在包含({“最小数量”，“正确猜测的结果”}) ylabel (“概率”）%获胜概率b(结束)

Ans = 1.8921e-11

玩百分比:一个无聊但有效的策略

那么什么是最优猜测策略?我们需要确定dist_guess这样p是最大化。但是，作为一个分布，的元素dist_guess需要加1(并且在0和1之间)。这是一个约束优化问题。目标函数为p，是线性的dist_guess．因此,使用linprog从优化工具箱，

Dist_guess = linprog(-dist_historic'，[]，[]，.．.(1、5)1 0(5、1),1 (1))

优化终止。Dist_guess = 0.0000 0.0000 0.0000 0.0000 1.0000

作为一个线性问题，其解位于凸可行域的一个顶点上。因此，最好的策略就是一直猜测最有可能的结果。这个做得怎么样?理论结果如下:p= 0.6(意味着平均正确29/48)。

2015年的实际情况会如何?鉴于我们猜测每场比赛都有13个以上的主队获胜，我们只需要知道2015年发生了多少这样的结果。

Numcorrect = sum(当前。Result == wincats{5}) frcorrect = numcorrect/48

Numcorrect = 26 frcorrect = 0.5417

作为比较，应该指出的是，至少使用一些橄榄球的知识，我个人预测……27个结果正确!是的，我可以简单地预测每场比赛都有13+的主队获胜。(除非TAB将他们的数据公开，否则我不知道这与其他人相比如何。)

全职:谁赢了?

概率有时是违反直觉的。每次都猜同样的事情肯定不是最好的获胜方式吧?当然，大多数时候你会得到正确的答案，但你也一定会有错误的时候，对吧?除了没有概率的保证。如果匹配结果本身是给定分布的随机变量(dist_historic)，则总是猜测相同结果而得到48个正确预测的概率与随机选择的48个游戏有该结果的概率相同。

Rng (2015) nexp = 1e5;边= cumsum([0 dist_historic]);Simresults = rand(48,nexp);Simresults =离散化(Simresults,edges，“分类”, wincats);num13plusHome = sum(simresults == wincats{5});次要情节(1 1 1)直方图(num13plusHome,“BinMethod”，“整数”，“归一化”，“pdf”)包含(“正确猜测结果的数目”) ylabel (“概率”) b = binopdf(k,48,p);持有在情节(k, b)从

因此，赢得TAB奖金的概率是，

最佳机会= b(结束)

最佳机会= 1.8921e-11

比3 * 10^{-34}美元要好，但仍然很糟糕——500亿分之一的糟糕。如果我们把这个数字作为一个选手正确预测所有48个结果(不管他们的策略)的概率的代表数字，那么任何人获胜的概率为

Anywin = 1 - binopdf(0,48000，最好的机会)

Anywin = 9.0820e-07

如果TAB多次举办这种比赛，每次有48,000名参赛者，他们每次的预期(平均)奖金将是

avgpay = anywin*1e6

avg股利= 0.9082

1美元对于48,000人来说是不错的广告!

你能做得更好吗?

当然，我应该能做出比27/48正确的预测更好的预测。但如何?咨询金刚鹦鹉里奇(橄榄球对章鱼保罗的回应)?或者使用MATLAB构建更好的策略。统计数据?机器学习?某种排名系统?如果你能想出一个比我猜得更准的策略(我不确定我在这方面设定了一个特别高的标准)，请告诉我在这里．

获取MATLAB代码

发布与MATLAB®R2015b