用广义线性模型拟合数据
这个例子展示了如何使用glmfit和glmval. 普通线性回归可用于将直线或其参数为线性的任何函数拟合到具有正态分布误差的数据。这是最常用的回归模型;然而,这并不总是现实的。广义线性模型以两种方式扩展了线性模型。首先,通过引入连接函数,放松了参数线性假设。其次,可以对非正态分布的误差分布进行建模
广义线性模型
回归模型根据一个或多个预测变量(通常表示为x1、x2等)定义响应变量(通常一般表示为y)的分布。最常用的回归模型为普通线性回归,模型y为正态随机变量,其均值为预测因子b0+b1*x1+…,其方差为常数。在单个预测因子x的最简单情况下,该模型可表示为关于每个poi的高斯分布的直线新界。
mu=@(x)-1.9+.23*x;x=5:1:15;yhat=mu(x);dy=-3.5:1:3.5;sz=size(dy);k=(长度(dy)+1)/2;x1=7*one(sz);y1=mu(x1)+dy;z1=normpdf(y1,mu(x1),1;x2=10*one(sz);y2=mu(x2)+);z2=normpdf(y2,mu,mu(x2),1);x3=mu(x3,my3,mu),xm,x),x(x),x),“b -”,...(x1, y1, z1,的r -, x1([k k]),y1([k k]),[0 z1(k)],r:',...x2, y2、z2的r -, x2([k k]),y2([k k]),[0 z2(k)],r:',...x3, y3、z3、的r -, x3([k k]),y3([k k]),[0 z3(k)],r:');zlim ([0 1]);包含(“X”);ylabel (“是的”);zlabel (“概率密度”);网格在;视图(45 [-45]);

在广义线性模型中,响应的均值被建模为预测器g(b0 + b1*x1 +…)的线性函数的单调非线性变换。变换g的逆称为“连杆”函数。示例包括logit (sigmoid)链接和log链接。y也可以是非正态分布,如二项分布或泊松分布。例如,具有对数链接和单个预测器x的泊松回归可以表示为每一点具有泊松分布的指数曲线。
mu=@(x)exp(-1.9+.23*x);x=5:1:15;yhat=mu(x);x1=7个一(1,5);y1=0:4;z1=poisspf(y1,mu(x1));x2=10个一(1,7);y2=0:6;z2=poisspf(y2,mu(x2));x3=13*1(1,9);y3=0:8;z3=poisspf(y3,mu(x3));图3(x,yhat,零(尺寸(x)),“b -”,...[x1;x1],[日元;y1]、[z1;0(大小(y1))),的r -(x1, y1, z1,“r”。,...[x2;x2]、[y2;y2]、[z2;0(大小(y2))),的r -x2, y2, z2,“r”。,...[x3;x3]、[y3;y3]、[z3;0(大小(y3))),的r -z3、x3 y3,“r”。);zlim ([0 1]);包含(“X”);ylabel (“是的”);zlabel (“概率”);网格在;视图(45 [-45]);

拟合Logistic回归
这个例子涉及一个实验,以帮助模拟各种重量的汽车的比例,未能通过里程测试。这些数据包括对重量、测试车辆数量和失败车辆数量的观察。
%一套汽车衡重量=[2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300];每一重量测试的汽车数量已测试= [48 42 31 34 31 21 23 23 21 16 17 21]';每一重量未通过测试的汽车数量失败=[120388141719151721];每一重量所对应的汽车失败的比例比例=失败/测试;情节(重量、比例、“年代”)包含(“重量”);ylabel (“比例”);

这张图是失败汽车比例的曲线图,它是重量的函数。可以合理地假设失效计数来自二项分布,概率参数P随重量增加而增加。但P究竟应该如何依赖于重量呢?
我们可以试着用一条直线来拟合这些数据。
linearCoef = polyfit(重量比例1);linearFit = polyval (linearCoef、重量);情节(重量、比例、“年代”、重量、linearFit的r -, [2000 4500],[0 0],“k:”, [2000 4500],[1 1],“k:”)包含(“重量”);ylabel (“比例”);

这种线性拟合存在两个问题:
1) 该行预测的比例小于0且大于1。
2)比例不是正态分布,因为它们必然有界。这违背了拟合简单线性回归模型所需的假设之一。
使用高阶多项式似乎会有所帮助。
[cubicCoef,统计,ctr] = polyfit(重量、比例、3);cubicFit = polyval (cubicCoef、重量、[],ctr);情节(重量、比例、“年代”、重量、cubicFit的r -, [2000 4500],[0 0],“k:”, [2000 4500],[1 1],“k:”)包含(“重量”);ylabel (“比例”);
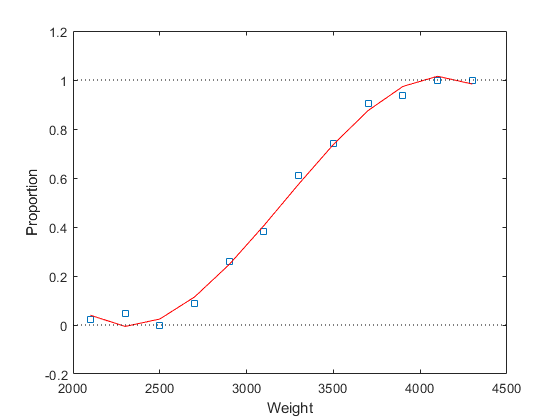
然而,这种契合仍然存在类似的问题。由图可知,当权重大于4000时,拟合比例开始减小;事实上,当权重值较大时,它将变为负值。当然,正态分布的假设仍然被违背了。
相反,更好的方法是使用glmfit拟合logistic回归模型。逻辑回归是广义线性模型的特例,对于这些数据比线性回归更合适,原因有二。首先,它使用适合于二项分布的拟合方法。其次,逻辑链接将预测比例限制在[0,1]范围内。
对于逻辑回归,我们指定预测器矩阵,和一个矩阵,其中一列包含失败计数,一列包含测试数。我们还指定了二项分布和logit链接。
[logitCoef,dev] = glmfit(weight,[failed tested],“二”,分对数的);logitFit = glmval (logitCoef、重量、分对数的);情节(重量、比例、“废话”、重量、logitFit的r -);包含(“重量”);ylabel (“比例”);
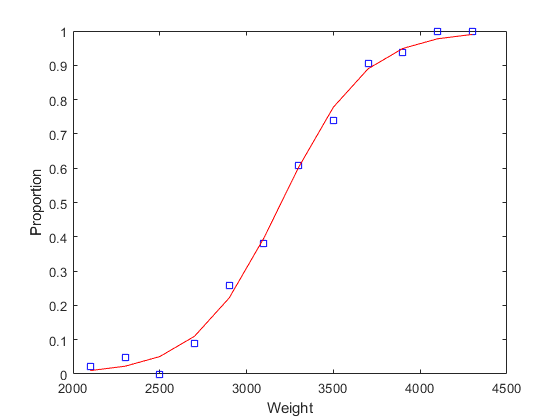
如图所示,当权重变小或变大时,拟合的比例渐近线为0和1。
模型诊断
的glmfit函数提供了许多用于检查拟合和测试模型的输出。例如,我们可以比较两个模型的偏差值,以确定平方项是否会显著改善拟合。
[logitCoef2,dev2] = glmfit([weight权重。^ 2],(未测试)“二”,分对数的);Pval = 1 - chi2cdf(dev-dev2,1)
pval=0.4019
较大的p值表明,对于这些数据,二次项并不能显著改善拟合。两种拟合的图显示,两者的拟合差别不大。
logitCoef2 = glmval(logitCoef2,[weight weight.^2],分对数的);情节(重量、比例、“废话”、重量、logitFit的r -,重量,物流配送2,“g -”);传奇(“数据”,“线性条件”,线性和二次项,“位置”,“西北”);
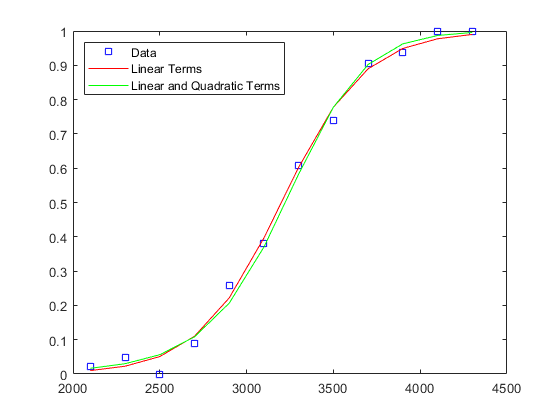
为了检验拟合的好坏,我们还可以看皮尔逊残差的概率图。这些都是标准化的,当模型与数据合理匹配时,它们有一个大致的标准正态分布。(如果没有这个标准化,残差就会有不同的方差。)
[logitcef,dev,stats]=glmfit(重量,[测试失败],“二”,分对数的);normplot (stats.residp);

残差图与正态分布符合得很好。
评估模型预测
一旦我们对模型感到满意,我们就可以用它来进行预测,包括计算置信范围。在这里,我们预测了在100辆被测试的汽车中,在四种重量下每一种都无法通过里程测试的预期数量。
weightPred = 2500:500:4000;[failedPred dlo,济]= glmval (logitCoef weightPred,分对数的统计,.95,100);dlo errorbar (weightPred failedPred,济,':');

二项模型的连接函数
对于这五个分布中的每一个glmfit金宝app支持,有一个规范(默认)链接函数。对于二项分布,规范链接是logit。但是,对于二项模型,还有三个其他链接是合理的。所有四个链接都在区间[0,1]内保持平均响应。
η= 5:.1:5;Plot (eta,1 ./ (1 + exp(-eta))“- - -”,eta,正常CDF(eta),“- - -”,...η1 - exp (exp (eta)),“- - -”,预计到达时间,预计到达时间(-exp(预计到达时间)),“- - -”);包含(“预测器的线性函数”);ylabel (“预测平均响应”);传奇(分对数的,“probit”,“补充日志”,“对数”,“位置”,“东”);

例如,我们可以将probit链接的匹配与logit链接的匹配进行比较。
probitCoef = glmfit(重量,[测试失败],“二”,“probit”);probitFit = glmval (probitCoef、重量、“probit”);情节(重量、比例、“废话”、重量、logitFit的r -、重量、probitFit“g -”);传奇(“数据”,“罗吉特模型”,“概率模型”,“位置”,“西北”);
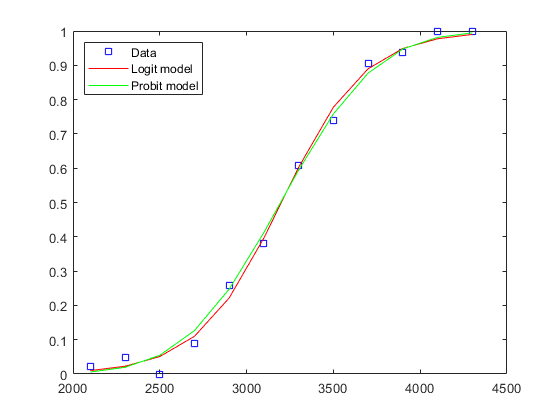
数据通常很难区分这四个连接函数,而且选择通常是基于理论基础。

