计算定点arctan
这个例子展示了如何使用CORDIC算法、多项式近似和查找表方法来计算定点,四象限反切线。这些实现是MATLAB®内置函数的近似值量化.一个有效的定点arctan算法来估计角度是许多应用的关键,包括机器人的控制,无线通信中的频率跟踪等等。
计算量化(y, x)使用CORDIC算法
简介
的cordicatan2函数近似MATLAB®量化函数,使用基于cordic的算法。CORDIC是坐标旋转数字计算机的首字母缩写。基于Givens旋转的CORDIC算法(见[1,2])是硬件效率最高的算法之一,因为它只需要迭代的shift-add操作。CORDIC算法消除了显式乘法器的需要,适用于计算各种函数,如正弦、余弦、反正弦、反余弦、反正切、矢量幅值、除、平方根、双曲和对数函数。
CORDIC矢量计算模式
CORDIC矢量模式方程被广泛用于计算(y / x)每股.在矢量模式下,CORDIC旋转器将输入矢量旋转到正x轴,以最小化 残差向量的分量。对于每次迭代,如果
残差向量的分量。对于每次迭代,如果 残差矢量坐标为正,CORDIC旋转器顺时针旋转(使用负角度);否则,它逆时针旋转(使用正角度)。如果角度累加器初始化为0,在迭代结束时,累积的旋转角度就是原始输入向量的角度。
残差矢量坐标为正,CORDIC旋转器顺时针旋转(使用负角度);否则,它逆时针旋转(使用正角度)。如果角度累加器初始化为0,在迭代结束时,累积的旋转角度就是原始输入向量的角度。
在矢量模式下,CORDIC方程为:


 是角度累加器吗
是角度累加器吗
在哪里 如果
如果 ,
, 否则;
否则;
 ,
, 是迭代的总数。
是迭代的总数。
作为 方法
方法 :
:




如上所述,可以使用矢量模式CORDIC rotator直接计算arctan,并将角度累加器初始化为零,即: 而且
而且 .
.
理解CORDICATAN2代码
简介
的cordicatan2函数计算x和y元素的四象限arctan,其中 .
.cordicatan2根据上面的CORDIC方程,使用矢量模式CORDIC算法计算arctan。
初始化
的cordicatan2函数执行以下初始化步骤:
 设置为初始X输入值。
设置为初始X输入值。 设置为Y的初始输入值。
设置为Y的初始输入值。 设置为0。
设置为0。
后 迭代时,这些初始值会导致
迭代时,这些初始值会导致
共享定点和浮点CORDIC内核代码
CORDIC算法(矢量模式)内核部分的MATLAB代码如下(对于标量的情况x,y,z).这段代码用于定点和浮点运算:
函数[x, y, z] = cordic_vectoring_kernel(x, y, z, inpLUT, n)对N个内核迭代执行CORDIC矢量内核算法。XTMP = x;Ytmp = y;为Idx = 1:n如果Y < 0 x(:) = x - ytmp;Y (:) = Y + xtmp;z(:) = z - inpLUT(idx);其他的X (:) = X + ytmp;Y (:) = Y - xtmp;z(:) = z + inpLUT(idx);结束XTMP = bitsra(x, idx);% bit-shift-right for乘以2^(-idx)Ytmp = bitsra(y, idx);% bit-shift-right for乘以2^(-idx)结束
可视化矢量模式CORDIC迭代
CORDIC算法通常通过指定的(常量)迭代次数运行,因为过早结束CORDIC迭代将破坏流水线代码,并且CORDIC收益 不是常数,因为
不是常数,因为 会有所不同。
会有所不同。
对于非常大的值 时,CORDIC算法保证收敛,但并不总是单调收敛。如下面的示例所示,中间迭代偶尔会比下面的迭代更靠近正x轴旋转向量。您通常可以通过增加迭代的总数来获得更高的精度。
时,CORDIC算法保证收敛,但并不总是单调收敛。如下面的示例所示,中间迭代偶尔会比下面的迭代更靠近正x轴旋转向量。您通常可以通过增加迭代的总数来获得更高的精度。
例子
在下面的例子中,迭代5提供了比迭代6更好的角度估计,并且CORDIC算法在后面的迭代中收敛。
用angle初始化输入向量 角度,大小= 1
角度,大小= 1
origFormat = get(0,“格式”);%存储原始格式设置;%在结束时恢复此设置。格式短%= 43*pi/180;%输入角度(以弧度为单位)镍= 10;迭代次数%inX = cos(theta);输入向量的% x坐标inY = sin(theta);输入向量的% y坐标%%预分配内存zf =零(1,镍);xf = [inX, 0 (1, Niter)];yf = [inY, zero (1, Niter)];angleLUT = atan(2.^-(0:Niter-1));%预计算角度查找表%调用CORDIC矢量内核算法为k = 1:Niter [xf(k+1), yf(k+1), zf(k)] = fixed.internal.cordic_vectoring_kernel_private(inX, inY, 0, angleLUT, k);结束
下面的输出显示了经过10次迭代的CORDIC角度积累(以度为单位)。请注意,第5次迭代产生的误差小于第6次迭代,并且计算出的角度很快收敛到实际输入角度。
angleAccumulator = zf*180/pi;angleError = angleAccumulator - theta*180/pi;流('迭代:%2d,计算角度:%7.3f,误差在度:%10g,误差在位:%g\n',...[(1:硝酸钠);angleAccumulator(:)”;angleError(:)”;log2 (abs (zf(:)的θ))));
迭代:1、计算角度:45.000,角度误差:2、比特数误差:-4.84036迭代:2、计算角度:18.435,角度误差:-24.5651,比特数误差:-1.22182迭代:3、计算角度:32.471,角度误差:-10.5288,比特数误差:-2.44409迭代:4、计算角度:39.596,角度误差:-3.40379,比特数误差:-4.07321迭代:5、计算角度:43.173,角度误差:0.172543,比特数误差:-8.37533迭代:6,计算角度:41.383,误差在角度:-1.61737,误差在位:-5.14671迭代:7,计算角度:42.278,误差在度:-0.722194,误差在位:-6.3099迭代:8,计算角度:42.725,误差在度:-0.27458,误差在位:-7.70506迭代:9,计算角度:42.949,误差在度:-0.0507692,误差在位:-10.1403迭代:10,计算角度:43.061,误差在度:0.0611365,误差在位:-9.87218
当N接近时 , CORDIC旋转增益
, CORDIC旋转增益 1.64676方法。在这个例子中,输入
1.64676方法。在这个例子中,输入 在单位圆上,所以初始旋转器的大小是1。下面的输出显示了经过10次迭代的旋转器的大小:
在单位圆上,所以初始旋转器的大小是1。下面的输出显示了经过10次迭代的旋转器的大小:
rotatorMagnitude =√(xf.^2+yf.^2);% CORDIC旋转器通过迭代获得流('迭代:%2d,旋转器大小:%g\n',...((0:硝酸钠);rotatorMagnitude (:)));
迭代:0,旋转器震级:1迭代:1,旋转器震级:1.41421迭代:2,旋转器震级:1.58114迭代:3,旋转器震级:1.6298迭代:4,旋转器震级:1.64248迭代:5,旋转器震级:1.64569迭代:6,旋转器震级:1.64649迭代:7,旋转器震级:1.64669迭代:8,旋转器震级:1.64674迭代:9,旋转器震级:1.64676迭代:10,旋转器震级:1.64676
请注意, 趋于0,且
趋于0,且 方法
方法 因为
因为 .
.
Y_n = yf(end)
Y_n = -0.0018
X_n = xf(end)
X_n = 1.6468
Figno = 1;fidemo。fixpt_atan2_demo_plot(figno, xf, yf)%矢量模式CORDIC迭代

Figno = Figno + 1;%累积角度和旋转幅度通过迭代fidemo。fixpt_atan2_demo_plot(figno,Niter, theta, angleAccumulator, rotatorMagnitude)

对CORDIC算法进行整体误差分析
总体误差由两部分组成:
由于CORDIC旋转角度由有限个基本角度表示而导致的算法错误。
由于角查找表的有限精度表示和用于定点运算的有限精度算法而产生的量化或舍入误差。
计算CORDIC算法错误
Theta = (-178:2:180)*pi/180;%以弧度表示的角度inXflt = cos(theta);%生成输入向量inYflt = sin(theta);镍= 12;总迭代次数的%zflt = cordicatan2(inYflt, inXflt, Niter);%浮点结果
通过将CORDIC计算与内置计算进行比较,计算CORDIC算法错误的最大幅度量化函数。
格式长cordic_algErr_real_world_value = max(abs(atan2(inYflt, inXflt) - zflt))))
cordic_algErr_real_world_value = 4.753112306290497e-04
以2为底的对数误差与迭代次数有关。在这个例子中,我们使用了12次迭代(即精确到11位二进制数字),因此误差的大小小于
cordic_algErr_bits = log2(cordic_algErr_real_world_value)
cordic_algErr_bits = -11.038839889583048
迭代次数与精度的关系
一旦量化误差大于总体误差,即量化误差大于算法误差,增加迭代总次数不会显著降低定点CORDIC算法的总体误差。你应该选择你的分数长度和迭代的总数,以确保量化误差小于算法误差。在CORDIC算法中,每迭代一次,精度提高一位。因此,没有理由选择大于输入数据精度的迭代次数。
另一种观察迭代次数和精度之间关系的方法是在算法的右移步中。例如,逆时针旋转
X (:) = x0 - bitsra(y,i);Y (:) = Y + bitsra(x0,i);
如果I等于y和x0的字长,那么bitsra (y,我)而且bitsra (x0,我)一直平移到0,不要对下一步做出任何贡献。
要测量来自定点算法的误差,而不是输入值的差异,请使用与定点CORDIC算法相同的输入计算浮点引用。
inXfix = sfi(inXflt, 16, 14);inYfix = sfi(inYflt, 16, 14);zref = atan2(double(inYfix), double(inXfix));zfix8 = cordicatan2(inYfix, inXfix, 8);zfix10 = cordicatan2(inYfix, inXfix, 10);zfix12 = cordicatan2(inYfix, inXfix, 12);zfix14 = cordicatan2(inYfix, inXfix, 14);zfix15 = cordicatan2(inYfix, inXfix, 15);Cordic_err = bsxfun(@minus,zref,double([zfix8;zfix10;zfix12;zfix14;zfix15]));
误差取决于迭代次数和输入数据的精度。在上面的例子中,输入数据的范围是[-1,+1],分数长度是14。从下面的表中显示了每次迭代的最大误差,以及图中显示了CORDIC算法的总体误差,您可以看到,在达到数据的精度之前,每次迭代误差都会减小约1位。
迭代= [8,10,12,14,15];max_cordicErr_real_world_value = max(abs(cordic_err'));流('迭代:%2d,真实世界值中的最大误差:%g\n',...[迭代;max_cordicErr_real_world_value]);
迭代:8,真实世界的最大误差值:0.00773633迭代:10,真实世界的最大误差值:0.00187695迭代:12,真实世界的最大误差值:0.000501175迭代:14,真实世界的最大误差值:0.000244621迭代:15,真实世界的最大误差值:0.000244621
max_cordicErr_bits = log2(max_cordicErr_real_world_value);流('迭代:%2d,最大误差位数:%g\n',(迭代;max_cordicErr_bits]);
迭代:8,最大错误比特:-7.01414迭代:10,最大错误比特:-9.05739迭代:12,最大错误比特:-10.9624迭代:14,最大错误比特:-11.9972迭代:15,最大错误比特:-11.9972
Figno = Figno + 1;fidemo。fixpt_atan2_demo_plot(figno, theta, cordic_err)

加速定点CORDICATAN2算法使用FIACCEL
您可以使用MATLAB®从MATLAB代码生成MEX函数fiaccel命令。通常,运行生成的MEX函数可以提高仿真速度,尽管实际速度的提高取决于所使用的仿真平台。下面的例子展示了如何加速定点cordicatan2算法使用fiaccel.
的fiaccel函数将MATLAB代码编译为MEX函数。这一步需要创建一个临时目录,并在该目录中具有写权限。
tempdirObj = fidemo.fiTempdir(“fixpt_atan2_demo”);
当您声明迭代次数为常数时(例如,12)使用coder.newtype(“常数”,12),编译后的角度查找表也将是常数,因此不会在每次迭代中计算。同样,当您调用已编译的MEX文件时cordicatan2_mex,您将不需要为迭代次数提供输入参数。如果传入迭代次数,则MEX函数将出错。
输入参数的数据类型决定是否cordicatan2函数执行定点或浮点计算。当MATLAB为该文件生成代码时,仅为特定的数据类型生成代码。例如,如果输入是定点,则只生成定点代码。
inp = {inYfix, inXfix, code .newtype(“不变”12)};%示例函数的输入fiaccel (“cordicatan2”,“o”,“cordicatan2_mex”,“参数”,输入)
首先,计算一个4象限的向量量化通过调用cordicatan2.
Tstart = tic;cordicatan2 (inYfix inXfix、硝石);telapsed_Mcordicatan2 = toc(tstart);
接下来,计算一个4象限的向量量化通过调用mex函数cordicatan2_mex.
cordicatan2_mex (inYfix inXfix);加载MEX文件Tstart = tic;cordicatan2_mex (inYfix inXfix);telapsed_MEXcordicatan2 = toc(tstart);
现在,比较一下速度。在MATLAB命令窗口中输入以下命令,查看特定平台上的速度改进:
fiaccel_speedup = telapsed_Mcordicatan2/telapsed_MEXcordicatan2;
使用实例清理临时目录。
清晰的cordicatan2_mex;status = tempdirObj.cleanUp;
计算量化(y, x)使用切比雪夫多项式逼近
多项式逼近是一种以乘累加(MAC)为中心的算法。它可以是一个很好的选择DSP实现的非线性函数,如(x)每股.
对于一个给定的多项式,和一个给定的函数F (x) = atan(x)在区间[-1,+1]上求值,多项式逼近理论试图找到使的最大值最小化的多项式 ,在那里
,在那里P (x)是近似多项式。一般来说,你可以通过用切比雪夫多项式来近似给定函数,并在所需的次数上截断多项式,从而获得非常接近最优多项式的多项式。
用第一类切比雪夫多项式在[-1,+1]区间上逼近arctan,总结如下式:

在哪里

![$$ x \in [-1, +1] $$](http://www.tatmou.com/help/examples/fixedpoint_product/win64/fixpt_atan2_demo_eq01792820127203503506.png)



因此,三阶切比雪夫多项式近似为

五阶切比雪夫多项式近似为

七阶切比雪夫多项式近似为

根据arctan函数的性质,通过角度修正可以得到四象限输出。
CORDIC算法与多项式逼近算法的算法误差比较
一般来说,多项式近似度越高,最终结果越准确。然而,更高的多项式近似度也增加了算法的复杂性,需要更多的MAC操作和更多的内存。与CORDIC算法和MATLAB一致量化函数时,输入参数由两者组成x而且y坐标而不是比率y / x.
为了消除量化误差,在下面的比较中使用了CORDIC和Chebyshev多项式近似算法的浮点实现。算法误差比较表明,增加CORDIC迭代次数可以减少误差。结果表明,12次迭代的CORDIC算法比5阶切比雪夫多项式近似的角度估计略好。三阶切比雪夫多项式的近似误差大约是五阶切比雪夫多项式的8倍。您应该根据所需的角度估计精度和硬件约束来选择多项式的阶数或阶数。
切比雪夫多项式近似的系数(x)每股按升序显示x.
constA3 = [0.970562748477141, -0.189514164974601];%三级constA5 = [0.994949366116654,-0.287060635532652,0.078037176446441];%第5次constA7 = [0.999133448222780 -0.320533292381664 0.144982490144465 ....-0.038254464970299);% 7阶Theta = (-90:1:90)*pi/180;%以弧度表示的角度inXflt = cos(theta);inYflt = sin(theta);zfltRef = atan2(inYflt, inXflt);% ATAN2函数的理想输出zfltp3 = fidemo.poly_atan2(inYflt,inXflt,3,constA3);%三阶多项式zflt5 = fidemo.poly_atan2(inYflt,inXflt,5,constA5);%五阶多项式zfltp7 = fidemo.poly_atan2(inYflt,inXflt,7,constA7);%七阶多项式zflt8 = cordicatan2(inYflt, inXflt, 8);% CORDIC alg与8次迭代zflt12 = cordicatan2(inYflt, inXflt, 12);% CORDIC alg与12迭代
CORDIC算法在8次和12次迭代时的最大算法误差幅度(或算法误差的无穷范数)如下所示:
cordic_algErr = [zfltRef;zfltRef] - [zflt8;zflt12];max_cordicAlgErr = max(abs(cordic_algErr'));流('迭代:%2d, CORDIC算法错误在真实世界值:%g\n',...[[8 12];max_cordicAlgErr (:)));
迭代:8,CORDIC算法错误在真实世界值:0.00772146迭代:12,CORDIC算法错误在真实世界值:0.000483258
log以2为底的误差表示精度的二进制位数。第12次迭代的CORDIC算法的估计角度精度为 :
:
max_cordicAlgErr_bits = log2(max_cordicAlgErr);流('迭代:%2d, CORDIC算法错误位:%g\n',...[[8 12];max_cordicAlgErr_bits (:)));
迭代:8,CORDIC算法错误在位:-7.01691迭代:12,CORDIC算法错误在位:-11.0149
下面的代码显示了阶3、阶5和阶7的多项式近似的最大算法误差的大小:
poly_algErr = [zfltRef;zfltRef;zfltRef] - [zfltp3;zfltp5;zfltp7];max_polyAlgErr = max(abs(poly_algErr'));流('阶数:%d,多项式逼近算法误差在真实世界值:%g\n',...[3:2:7;max_polyAlgErr (:)));
阶数:3,真实世界值多项式逼近算法误差:0.00541647阶数:5,真实世界值多项式逼近算法误差:0.000679384阶数:7,真实世界值多项式逼近算法误差:9.16204e-05
log以2为底的误差表示精度的二进制位数。
max_polyAlgErr_bits = log2(max_polyAlgErr);流('阶数:%d,多项式逼近算法误差:%g\n',...[3:2:7;max_polyAlgErr_bits (:)));
Order: 3,多项式逼近算法误差(比特):-7.52843 Order: 5,多项式逼近算法误差(比特):-10.5235 Order: 7,多项式逼近算法误差(比特):-13.414
Figno = Figno + 1;fidemo。fixpt_atan2_demo_plot(figno, theta, cordic_algErr, poly_algErr)

浮点切比雪夫多项式逼近算法到不动点的转换
假设输入和输出字长度被硬件限制为16位,并使用5阶切比雪夫多项式进行近似。因为输入的动态范围x,y而且y / x都在[-1,+1]之内,则可以通过选择字长为16位、分数长为14位的带符号定点输入数据类型来避免溢出。多项式的系数是纯分数,并且在(-1,+1)之内,因此我们可以选择它们的数据类型为带符号的固定点,字长为16位,分数长度为15位(精度最好)。算法的鲁棒性在于 在[-1,+1]范围内,系数和的乘法
在[-1,+1]范围内,系数和的乘法 在(-1,+1)内。因此,动态范围不会增长,并且由于预先确定的定点数据类型,预计不会溢出。
在(-1,+1)内。因此,动态范围不会增长,并且由于预先确定的定点数据类型,预计不会溢出。
类似CORDIC算法,基于四象限多项式逼近量化算法输出估计的角度![$$ [-\pi, \pi] $$](http://www.tatmou.com/help/examples/fixedpoint_product/win64/fixpt_atan2_demo_eq16108843240809288879.png) .因此,我们可以选择一个13位的输出分数长度来避免溢出,并提供一个动态范围[-4,+3.9998779296875]。
.因此,我们可以选择一个13位的输出分数长度来避免溢出,并提供一个动态范围[-4,+3.9998779296875]。
arctan在区间[-1,+1]上的基本浮点切比雪夫多项式近似被实现为chebyPoly_atan_fltpt的局部函数。poly_atan2.m文件。
函数z = chebyPoly_atan_fltpt(y,x,N,constA,Tz,RoundingMethodStr)
TMP = y/x;开关N case 3z = constA(1)*tmp + constA(2)*tmp^3;case 5 z = constA(1)*tmp + constA(2)*tmp^3 + constA(3)*tmp^5;case 7z = constA(1)*tmp + constA(2)*tmp^3 + constA(3)*tmp^5 + constA(4)*tmp^7;否则disp(' Chebysh金宝appev多项式的支持阶为3,5,7 ');结束
arctan在区间[-1,+1]上的基本定点切比雪夫多项式近似被实现为chebyPoly_atan_fixpt的局部函数。poly_atan2.m文件。
函数z = chebyPoly_atan_fixpt(y,x,N,constA,Tz,RoundingMethodStr)
z = fi(0,'numerictype', Tz, 'RoundingMethod', RoundingMethodStr);Tx =数字类型(x);tmp = fi(0, 'numerictype',Tx, 'RoundingMethod', RoundingMethodStr);tmp(:) = Tx.divide(y, x);% y / x;
tmp2 = fi(0, 'numerictype',Tx, 'RoundingMethod', RoundingMethodStr);tmp3 = fi(0, 'numerictype',Tx, 'RoundingMethod', RoundingMethodStr);Tmp2 (:) = tmp*tmp;% (y/x)^2 tmp3(:) = tmp2*tmp;% (y / x) ^ 3
z(:) = constA(1)*tmp + constA(2)*tmp3;对于N = 3阶
if (N == 5) || (N == 7) tmp5 = fi(0, 'numerictype',Tx, 'RoundingMethod', RoundingMethodStr);Tmp5 (:) = tmp3 * tmp2;% (y/x)^5 z(:) = z + constA(3)*tmp5;对于N = 5
如果N == 7 tmp7 = fi(0, 'numerictype',Tx, 'RoundingMethod', RoundingMethodStr);Tmp7 (:) = tmp5 * tmp2;% (y/x)^7 z(:) = z + constA(4)*tmp7;%for order N = 7 end结束
宇宙四象限量化计算采用切比雪夫多项式近似实现poly_atan2.m文件。
函数z = poly_atan2(y,x,N,constA,Tz,RoundingMethodStr)
if nargin < 5%浮点算法fhandle = @chebyPoly_atan_fltpt;Tz = [];RoundingMethodStr = [];Z = 0(大小(y));else %定点算法fhandle = @chebyPoly_atan_fixpt;%预分配输出z = fi(零(大小(y)), 'numerictype', Tz, 'RoundingMethod', RoundingMethodStr);结束
%应用角度校正获得四象限输出为idx = 1:长度(y) %第一象限如果abs(x(idx)) >= abs(y(idx)) % (0, pi/4] z(idx) = feval(fhandle, abs(y(idx)), abs(x(idx)), N, constA, Tz, RoundingMethodStr);else % (pi/4, pi/2) z(idx) = pi/2 - feval(fhandle, abs(x(idx)), abs(y(idx)), N, constA, Tz, RoundingMethodStr);结束
如果x(idx) < 0%第二和第三象限如果y(idx) < 0 z(idx) = -pi + z(idx);Else z(idx) = PI - z(idx);结束else %第四象限如果y(idx) < 0 z(idx) = -z(idx);结束结束
对多项式逼近算法进行总体误差分析
与CORDIC算法类似,多项式近似算法的总体误差由算法误差和量化误差两部分组成。在前一节中分析了多项式逼近算法的算法误差,并与CORDIC算法的算法误差进行了比较。
计算量化误差
通过比较定点多项式近似和浮点多项式近似来计算量化误差。
用收敛四舍五入量化输入和系数:
inXfix = fi(fi(inXflt, 1, 16, 14,“RoundingMethod”,“收敛”),“fimath”[]);inYfix = fi(fi(inYflt, 1,16,14,“RoundingMethod”,“收敛”),“fimath”[]);constAfix3 = fi(fi(constA3, 1,16,“RoundingMethod”,“收敛”),“fimath”[]);constAfix5 = fi(fi(constA5, 1,16,“RoundingMethod”,“收敛”),“fimath”[]);constAfix7 = fi(fi(constA7, 1,16,“RoundingMethod”,“收敛”),“fimath”[]);
计算量化误差的最大幅度地板上舍入:
Ord = 3:2:7;%使用三阶,五阶,七阶多项式Tz =数字类型(1,16,13);输出数据类型zfix3p = fidemo.poly_atan2(inYfix,inXfix,ord(1),constAfix3,Tz,“地板”);%三级zfix5p = fidemo.poly_atan2(inYfix,inXfix,ord(2),constAfix5,Tz,“地板”);%第5次zfix7p = fidemo.poly_atan2(inYfix,inXfix,ord(3),constAfix7,Tz,“地板”);% 7阶poly_quantErr = bsxfun(@minus, [zfltpp3;zfltp5;zfltp7], double([zfix3p;zfix5p;zfix7p]));max_polyQuantErr_real_world_value = max(abs(poly_quantErr'));max_polyQuantErr_bits = log2(max_polyQuantErr_real_world_value);流('PolyOrder: %2d,定量错误位:%g\n',...[奥德;max_polyQuantErr_bits]);
PolyOrder: 5,量化错误:-12.325 PolyOrder: 7,量化错误:-11.8416
计算总体误差
通过将定点多项式近似与内置近似进行比较来计算总体误差量化函数。理想的参考输出为zfltRef.由于输入数据、系数的有限精度和定点算术运算的舍入效应,7阶多项式逼近的总体误差主要由量化误差引起。
poly_err = bsxfun(@minus, zfltRef, double([zfix3p;zfix5p;zfix7p]));max_polyErr_real_world_value = max(abs(poly_err'));max_polyErr_bits = log2(max_polyErr_real_world_value);流('PolyOrder: %2d,总误差位数:%g\n',...[奥德;max_polyErr_bits]);
PolyOrder: 5,整体错误:-10.2497 PolyOrder: 7,整体错误:-11.5883
Figno = Figno + 1;fidemo。fixpt_atan2_demo_plot(figno, theta, poly_err)

多项式逼近中舍入模式的影响
与12次迭代、13位角累加器分数长度的CORDIC算法相比,五阶切比雪夫多项式近似给出了相似的量化误差阶数。在下面的例子中,最近的,轮而且收敛舍入模式给出的量化误差小于地板上舍入模式。
所使用的量化误差的最大幅度地板上舍入
poly5_quantErrFloor = max(abs(poly_quantErr(2,:)));poly5_quantErrFloor_bits = log2(poly5_quantErrFloor)
poly5_quantErrFloor_bits = -12.324996933210334
为了进行比较,计算量化误差的最大幅度使用最近的舍入:
zfixp5n = fidemo.poly_atan2(inYfix,inXfix,5,constAfix5,Tz,“最近的”);poly5_quantErrNearest = max(abs(zfltp5 - double(zfixp5n)));poly5_quantErrNearest_bits = log2(poly5_quantErrNearest) set(0,“格式”, origFormat);%重置MATLAB输出格式
poly5_quantErrNearest_bits = -13.175966487895451
计算量化(y, x)使用查找表
有许多基于查找表的方法可用于实现定点arctan近似。下面是一种基于单个实值查找表和简单的最近邻线性插值的低成本方法。
基于单查找表的方法
的量化方法fi对象在定点设计器™近似MATLAB®内置浮点量化函数,使用基于单一查找表的方法,并在值之间使用简单的最近邻线性插值。这种方法允许一个小的实值查找表,并使用简单的算术。
使用单个实值查找表简化了索引计算和实现非常准确的结果所需的整体算术。这些简化产生了相对较高的速度性能以及相对较低的内存需求。
基于查找表的理解量化实现
查找表的大小和准确性
查找表的两个重要设计考虑因素是它的大小和准确性。不可能为每一种可能创建一个表 输入值。由于查找表值的量化,也不可能完全准确。
输入值。由于查找表值的量化,也不可能完全准确。
作为妥协,量化定点设计器的方法fi对象使用8位查找表作为其实现的一部分。一个8位表只有256个元素长,所以它很小且高效。在许多平台上,8位也对应一个字节或一个单词的大小。与线性插值和16位输出(查找表值)精度结合使用,8位可寻址查找表提供了非常好的精度和性能。
算法实现概述
为了更好地理解定点设计器实现,首先考虑四象限的对称性量化(y, x)函数。如果你总是在x-y空间的第一个八分程中计算arctan(即,在角度0和/4弧度之间),那么你可以对任何y和x值的结果角执行八分程校正。
作为预处理部分的一部分,考虑y和x的符号和相对大小,并执行除法。根据y和x的符号和大小,只计算以下值中的一个:y/x, x/y, -y/x, -x/y, -y/-x, -x/-y。根据y和x的符号和大小的先验知识,计算保证非负且纯分数的无符号结果。该值使用无符号16位分数定点类型。
存储的纯分数无符号定点结果的无符号整数表示的8个最高有效位(msb)然后用于直接索引一个8位(长度-256)查找表值,其中包含0到pi/4弧度之间的角度值。执行两个表查找,一个在计算表索引位置lutValBelow,一个在下一个索引位置lutValAbove:
idxUint8MSBs = bitsliceget(idxUFIX16, 16,9);zeroBasedIdx = int16(idxUint8MSBs);(zeroBasedIdx + 1);lutValAbove = FI_ATAN_LUT(zeroBasedIdx + 2);
idxUFIX16的剩余8位最低有效位(lsb)用于在这两个表值之间进行插值。LSB值被视为具有8位分数数据类型的标准化缩放因子rFracNT:
rFracNT = numerictype(0,8,8);%分数余数数据类型idxfrac8lbs = reinterpretcast(bitsliceget(idxUFIX16,8,1), rFracNT);rFraction = idxfrac8lbs;
这两个查找表值和余数(rFraction)值用于执行简单的最近邻线性插值。实数乘法用于确定两点之间的加权差。这将导致一个简单的计算(相当于一个乘积和两个和),以获得插值的定点结果:
temp = rFraction * (lutValAbove - lutValBelow);rslt = lutValBelow + temp;
最后,基于y和x的原始符号和相对大小,使用简单的八进制修正逻辑和算法形成输出结果。将第一个八八分程[0,pi/4]角度值结果与常数加或减,形成八八分程校正的角度输出。
计算定点arctan使用量化
你可以致电量化函数直接使用定点或浮点输入。定点采用基于查找表的算法量化实现:
zFxpLUT = atan2(inYfix,inXfix);
计算总体误差
可以通过将基于定点查找表的近似值与内置近似值进行比较来计算总体误差量化函数。理想的参考输出为zfltRef.
lut_err = bsxfun(@minus, zfltRef, double(zFxpLUT));max_lutErr_real_world_value = max(abs(lut_err'));max_lutErr_bits = log2(max_lutErr_real_world_value);流('总误差:%g\n', max_lutErr_bits);
总体误差:-12.6743
Figno = Figno + 1;fidemo。fixpt_atan2_demo_plot(figno, theta, lut_err)

定点实现的总体误差比较
正如前面所做的,您可以通过比较定点近似值和内置近似值来计算总体误差量化函数。理想的参考输出为zfltRef.
zfixCDC15 = cordicatan2(inYfix, inXfix, 15);cordic_15I_err = bsxfun(@minus, zfltRef, double(zfixCDC15));poly_7p_err = bsxfun(@minus, zfltRef, double(zfix7p));Figno = Figno + 1;fidemo。fixpt_atan2_demo_plot(figno, theta, cordic_15I_err, poly_7p_err, lut_err)
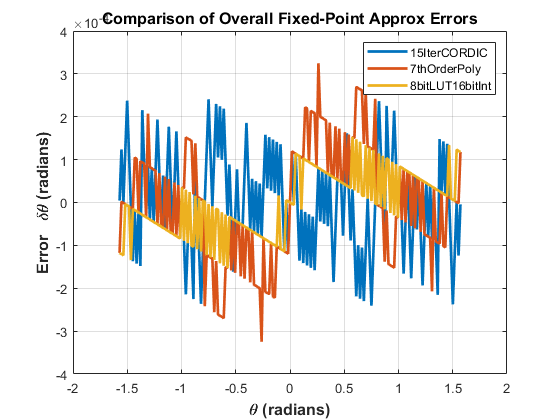
比较不动点逼近算法的代价
定点CORDIC算法需要进行如下操作:
1表查找每个迭代
2班每个迭代
3增加每个迭代
n阶定点切比雪夫多项式逼近算法需要进行如下操作:
1部
乘法(N + 1)
(n - 1) / 2添加
采用最近邻线性插值的简化单查表算法需要执行以下操作:
1部
2表查询
1乘法
2添加
在实际应用中,选择用于定点反切线计算的算法通常取决于所需的精度、成本和硬件限制。
关闭所有;%关闭所有图形窗口
参考文献
Jack E. Volder, CORDIC三角计算技术,IRE电子计算机学报,卷EC-8, 1959年9月,第330-334页。
Ray Andraka,基于FPGA的计算机CORDIC算法的调查,1998年ACM/SIGDA第六届现场可编程门阵列国际研讨会论文集,1998年2月22-24日,pp. 191-200。
% #好< * NOPTS >



