使用符号数学与优化工具箱™求解器

这个示例使用:

打开生活的脚本

这个例子展示了如何使用symbol Math Toolbox™函数雅可比矩阵和matlabFunction为优化求解人员提供分析导数。当你提供目标函数和约束函数的梯度和Hessians时，最优化工具箱™求解器通常更准确和高效。

基于问题的优化可以自动计算和使用梯度;看到优化工具箱中的自动微分．有关使用自动区分的基于问题的示例，请参见约束静电非线性优化，基于问题．

在使用优化函数的符号计算时，有几个注意事项:

优化目标和约束函数应该用向量来定义，例如x．然而，符号变量是标量或复数值，而不是向量值。这需要你在向量和标量之间进行转换。
优化梯度，有时是Hessians，应该在目标或约束函数体中计算。这意味着符号梯度或Hessian必须放置在目标或约束函数文件或函数句柄的适当位置。
象征性地计算梯度和Hessians是很耗时的。因此，您应该只执行一次这个计算，并通过matlabFunction，在求解器执行期间调用。
的符号表达式求值潜艇函数是耗时的。它使用起来更有效率matlabFunction．
matlabFunction生成依赖于输入向量方向的代码。自fmincon用列向量调用目标函数时，必须小心调用matlabFunction用符号变量的列向量。

第一个例子:无约束Hessian最小化

最小化的目标函数为:

$f （ x_{1} ， x_{2} ）＝日志（ 1 + 3. {（ x_{2} - （ x_{1}^{3.} - x_{1} ））}^{2} + （ x_{1} - 4 / 3. ）^{2} ）．$

这个函数是正的，在点处有一个唯一的最小值为零x1= 4/3,x2=(4/3)^3 - 4/3 = 1.0370…

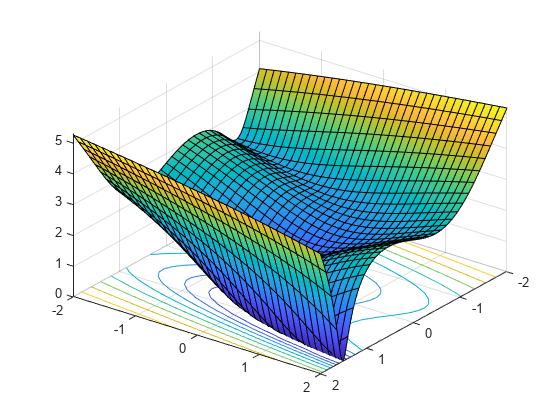
我们把自变量写成x1和x2因为在这种形式中，它们可以用作符号变量。作为向量的分量x他们会被写下来x (1)和x (2)．函数有一个曲折的山谷，如下图所示。

信谊x1x2真正的x = (x1, x2);%符号变量列向量日志(f = 1 + 3 * (x2 - (x1 ^ 3 - x1)) ^ 2 + (x1 - 4/3) ^ 2)

f =
                 
                   $日志 （ {(x_{1} - \frac{4}{3.})}^{2} + 3. {(- {x_{1}}^{3.} + x_{1} + x_{2})}^{2} + 1 ）$

fsurf (f (2 - 2),“ShowContours”，“上”38)视图(127)

图中包含一个坐标轴。坐标轴包含一个函数曲面类型的对象。

计算f的梯度和Hessian:

gradf =雅可比矩阵(f (x)。%列gradf

gradf =
                 
                   $\begin{array}{l} （ \begin{array}{c} - \frac{6 (3. {x_{1}}^{2} - 1) (- {x_{1}}^{3.} + x_{1} + x_{2}) - 2 x_{1} + \frac{8}{3.}}{σ_{1}} \\ \frac{- 6 {x_{1}}^{3.} + 6 x_{1} + 6 x_{2}}{σ_{1}} \end{array} ） \\ 在哪里 \\ σ_{1} ＝ {(x_{1} - \frac{4}{3.})}^{2} + 3. {(- {x_{1}}^{3.} + x_{1} + x_{2})}^{2} + 1 \end{array}$

hessf =雅可比矩阵(gradf, x)

hessf =
                 
                   $\begin{array}{l} （ \begin{array}{c} \frac{6 {(3. {x_{1}}^{2} - 1)}^{2} - 36 x_{1} (- {x_{1}}^{3.} + x_{1} + x_{2}) + 2}{σ_{2}} - \frac{{σ_{3.}}^{2}}{{σ_{2}}^{2}} & σ_{1} \\ σ_{1} & \frac{6}{σ_{2}} - \frac{{(- 6 {x_{1}}^{3.} + 6 x_{1} + 6 x_{2})}^{2}}{{σ_{2}}^{2}} \end{array} ） \\ 在哪里 \\ σ_{1} ＝ \frac{(- 6 {x_{1}}^{3.} + 6 x_{1} + 6 x_{2}) σ_{3.}}{{σ_{2}}^{2}} - \frac{18 {x_{1}}^{2} - 6}{σ_{2}} \\ σ_{2} ＝ {(x_{1} - \frac{4}{3.})}^{2} + 3. {(- {x_{1}}^{3.} + x_{1} + x_{2})}^{2} + 1 \\ σ_{3.} ＝ 6 (3. {x_{1}}^{2} - 1) (- {x_{1}}^{3.} + x_{1} + x_{2}) - 2 x_{1} + \frac{8}{3.} \end{array}$

的fminunc解算器希望传入一个向量x，然后SpecifyObjectiveGradient选项设置为真正的和HessianFcn选项设置为“目标”，期望一个包含三个输出的列表:(f (x), gradf (x) hessf (x))．

matlabFunction从一个包含三个输入的列表生成一个包含三个输出的列表。此外,使用var选项,matlabFunction接受向量输入。

跳频= matlabFunction (f, gradf hessf,“var”, {x});

现在求解从点[-1,2]开始的最小化问题:

选择= optimoptions (“fminunc”，．..“SpecifyObjectiveGradient”,真的,．..“HessianFcn”，“目标”，．..“算法”，“信赖域”，．..“显示”，“最后一次”）;[xfinal, fval exitflag、输出]= fminunc (fh、[1,2]选项)

局部最小值。Fminunc之所以停止，是因为函数值相对于初始值的最终变化小于函数的容差值。

xfinal =2×11.3333 - 1.0370

fval = 7.6623 e-12

exitflag = 3

输出=结构体字段:第一个迭代:3.4391e-05 algorithm: 'trust-region' message: '…“constrviolation: []

将其与不使用梯度或Hessian信息的迭代次数进行比较。这需要“拟牛顿”算法。

选择= optimoptions (“fminunc”，“显示”，“最后一次”，“算法”，“拟牛顿”）;fh2中= matlabFunction (f,“var”, {x});% fh2 =客观，无梯度或黑森[xfinal, fval exitflag output2] = fminunc (fh2中,[1,2]选项)

局部最小值。由于梯度的大小小于最优性公差的值，优化完成。

xfinal =2×11.3333 - 1.0371

fval = 2.1985 e-11

exitflag = 1

output2 =结构体字段:firstderopt: 2.4587e-06 algorithm: '拟牛顿' message: '…'

当使用梯度和Hessians时，迭代次数更少，函数计算也更少:

sprintf ([“使用渐变有%d次迭代”．..“和黑森，但没有他们。”]，．..output.iterations output2.iterations)

ans = '使用梯度和Hessian有14次迭代，但没有它们有18次。'

sprintf ([“使用梯度进行了%d函数评估”．..“和黑森，但没有他们。”]，．..output.funcCount output2.funcCount)

ans = '使用梯度和Hessian进行了15次函数评估，但没有使用梯度和Hessian的有81次。'

第二个例子:fmincon内点算法的约束最小化

我们考虑相同的目标函数和起点，但现在有两个非线性约束:

$5 \sinh （ x_{2} / 5 ） \geq x_{1}^{4}$

$5 双曲正切（ x_{1} / 5 ） \geq x_{2}^{2} - 1 ．$

约束使优化远离全局最小值点[1.333,1.037]。想象这两个约束条件:

(X, Y) = meshgrid (2: .01:3);Z = (5*sinh(y /5) >= X.^4);当满足第一个约束时，% Z=1，否则Z=0Z = Z+ 2*(5*tanh(X./5)) >= y ^2 - 1;% Z=2，其中第二个满足，Z=3，其中两个都满足冲浪(X, Y, Z,“线型”，“没有”）;无花果= gcf;fig.Color =' w '；%白色背景视图(0,90)在plot3(。43.96, .0373, 4,“o”，“MarkerEdgeColor”，“r”，“MarkerSize”8);%最佳点包含(“x”) ylabel (“y”)举行从

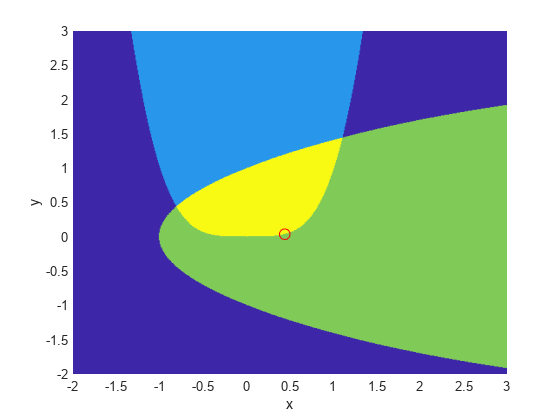
图中包含一个坐标轴。轴包含面、线两个对象。

我们在最优点周围画了一个红色的小圆。

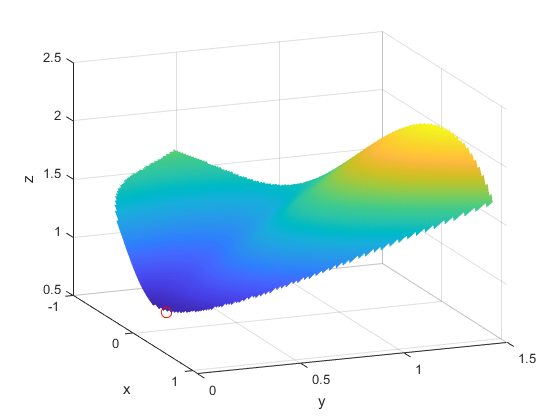
这是目标函数在可行区域上的图，这个区域满足两个约束条件，上图用暗红色表示，还有一个围绕最优点的红色小圆:

W = log(1 + 3) *(Y - (X ^3 - X))^2 + (x - 4/3) ^2;% W =目标函数W(Z < 3) = nan;%只在满足约束的地方绘图冲浪(X, Y, W,“线型”，“没有”）;视图(68年,20)在plot3(。43.96, .0373, .8152,“o”，“MarkerEdgeColor”，“r”，．..“MarkerSize”8);%最佳点包含(“x”) ylabel (“y”) zlabel (“z”)举行从

图中包含一个坐标轴。轴包含面、线两个对象。

非线性约束必须写成这种形式c (x) < = 0．我们计算所有的符号约束及其导数，并将它们放在一个函数句柄中matlabFunction．

约束的梯度应该是列向量;它们必须以矩阵的形式置于目标函数中，矩阵的每一列表示一个约束函数的梯度。这是这个形式的转置雅可比矩阵我们取下面的转置。

我们将非线性约束放入一个函数句柄中。fmincon期望非线性约束和梯度按顺序输出[c ceq gradc gradceq]．由于没有非线性等式约束，我们输出［］为量表信和gradceq．

C1 = x1^4 - 5*sinh(x2/5);C2 = x2^2 - 5*tanh(x1/5) - 1;C = [c1 c2];gradc =雅可比矩阵(c、x) ';把%转置成正确的形式约束= matlabFunction (gradc, c, [] [],“var”, {x});

内点算法要求其Hessian函数写成一个单独的函数，而不是目标函数的一部分。这是因为非线性约束函数需要在其Hessian中包含这些约束。它的黑森是拉格朗日的黑森;有关更多信息，请参阅用户指南。

Hessian函数有两个输入参数:位置向量x，以及拉格朗日乘子结构lambda。用于非线性约束的lambda结构的部分是lambda.ineqnonlin和lambda.eqnonlin．对于电流约束，没有线性等式，所以我们使用两个乘数lambda.ineqnonlin (1)和lambda.ineqnonlin (2)．

在第一个例子中，我们计算了目标函数的Hessian。现在我们计算这两个约束函数的Hessians，并使函数句柄版本为matlabFunction．

hessc1 =雅可比矩阵(gradc (: 1), x);%约束=第一个c列hessc2 =雅可比矩阵(gradc (:, 2), x);hessfh = matlabFunction (hessf,“var”, {x});hessc1h = matlabFunction (hessc1,“var”, {x});hessc2h = matlabFunction (hessc2,“var”, {x});

为了得到最后的Hessian，我们把三个Hessian放在一起，在约束函数中加入适当的拉格朗日乘数。

Myhess = @(x,lambda)(hessfh(x) +．..lambda.ineqnonlin (1) * hessc1h (x) +．..lambda.ineqnonlin (2) * hessc2h (x));

设置使用内点算法、梯度和Hessian的选项，使目标函数同时返回目标和梯度，并运行求解器:

选择= optimoptions (“fmincon”，．..“算法”，“内点”，．..“SpecifyObjectiveGradient”,真的,．..“SpecifyConstraintGradient”,真的,．..“HessianFcn”myhess,．..“显示”，“最后一次”）;% fh2 =不含黑森纤维的客观物fh2中= matlabFunction (f gradf“var”, {x});[xfinal, fval exitflag、输出]= fmincon (fh2中,[1,2],．..[],[],[],[],[],[], 约束,选项)

找到满足约束条件的局部最小值。优化完成是因为目标函数在可行方向上不减小到最优性公差的值内，约束条件满足到约束公差的值内。

xfinal =2×10.4396 - 0.0373

fval = 0.8152

exitflag = 1

输出=结构体字段:第一个迭代:10 funcCount: 13 construct: 0 stepsize: 1.9160e-06 algorithm: ' internal -point' firstderopt: 1.9217e-08 cgiterations: 0 message: '…'最佳可行:[1x1 struct]

再次，求解器使许多更少的迭代和函数计算梯度和Hessian提供比当他们不是:

选择= optimoptions (“fmincon”，“算法”，“内点”，．..“显示”，“最后一次”）;% fh3 =客观无梯度或黑森fh3 = matlabFunction (f,“var”, {x});%无梯度约束:约束= matlabFunction (c []“var”, {x});[xfinal, fval exitflag output2] = fmincon (fh3 [1, 2],．..[],[],[],[],[],[], 约束,选项)

找到目标函数值较低的可行点。找到满足约束条件的局部最小值。优化完成是因为目标函数在可行方向上不减小到最优性公差的值内，约束条件满足到约束公差的值内。

xfinal =2×10.4396 - 0.0373

fval = 0.8152

exitflag = 1

output2 =结构体字段:stepsize: 9.6632e-07 algorithm: ' internal -point' firstderopt: 3.8435e-07 cgiterations: 0 message: '…'最佳可行:[1x1 struct]

sprintf ([“使用渐变有%d次迭代”．..“和黑森，但没有他们。”]，．..output.iterations output2.iterations)

ans = '使用梯度和Hessian进行了10次迭代，但没有它们的情况下进行了18次。'

sprintf ([“使用梯度进行了%d函数评估”．..“和黑森，但没有他们。”]，．..output.funcCount output2.funcCount)

ans = '使用梯度和Hessian进行了13次函数评估，但没有使用它们的有57次。'

清理符号变量

本例中使用的符号变量被假定为实数。要从符号引擎工作区中清除这个假设，仅删除变量是不够的。您必须使用语法清除变量的假设

假设((x1, x2),“清楚”）

当以下命令的输出为空时，将清除所有假设

假设((x1, x2))

ans =空符号:1 × 0

使用符号数学与优化工具箱™求解器

第一个例子:无约束Hessian最小化

第二个例子:fmincon内点算法的约束最小化

清理符号变量

相关的话题

优化工具箱的文档

金宝app

8 MATLAB数据科学备忘单