薄板的非线性传热
该示例示出了如何执行薄板的传热分析。
板是正方形的,温度沿底边固定。没有热量从其他三条边传递(即它们是绝热的)。热通过对流和辐射从板的上、下表面传递。由于考虑了辐射,所以问题是非线性的。本例的目的之一是展示如何处理PDE问题中的非线性。
同时进行了稳态和瞬态分析。在稳态分析中,我们关心的是在平板达到平衡态后,在不同点上的最终温度。在瞬态分析中,我们感兴趣的是板内温度随时间的变化。这个瞬态分析可以回答的一个问题是,板块达到平衡温度需要多长时间。
平板的传热方程
该板的平面尺寸为1米乘1米,厚度为1厘米。由于平板相对于平面尺寸较薄,所以在厚度方向上温度可以假定为常数;结果的问题是2D的。
对流和辐射热传递被假定为采取该板的两个面和特定的环境温度之间进行。
热量从每个板面转移的每单位面积由于对流的量被定义为
哪里 为环境温度, 是在板表面上的特定的x和y位置处的温度,并 为规定的对流系数。
热量从每个板面转移的每单位面积由于辐射量被定义为
哪里 是脸部的发射率和 为斯蒂芬-玻尔兹曼常数。由于辐射传递的热量与表面温度的四次方成正比,所以这个问题是非线性的。
说明本薄板的温度PDE是
哪里 为材料密度, 是比热, 是板厚度,以及两个帐户,以便从两个板面上的热传递的因素。
为方便起见,改写由PDE工具箱预计形式此公式
问题设置
该板由铜,其具有以下性质中的:
K = 400;%的铜的热导率,W /(M-K)RHO = 8960;铜的%浓度,单位为kg /立方公尺specificHeat = 386;铜的%比热,J /(千克·K)厚= 0.01;板厚(米stefanBoltz = 5.670373 e-8;%斯蒂芬 - 玻尔兹曼常数,W /(平方公尺-K ^ 4)hCoeff = 1;%对流系数W /(平方公尺-K)%的环境温度被假定为300度开尔文。ta = 300;工作= 5;板面的发射率%
使用单个因变量创建PDE模型。
numberOfPDE = 1;模型= createpde(numberOfPDE);
对于正方形,所述几何形状和网眼容易定义为如下所示。
宽度= 1;身高= 1;
通过给出4个x位置和4个y位置的角来定义正方形。
gdm = [3 4 0 width width 0 0 0 height]';g = decsg (gdm,'S1', ('S1')');
转换DECSG几何成几何对象上这样它被附加到PDEModel
geometryFromEdges(模型中,g);
绘制几何图形并显示边界条件定义中使用的边缘标签。
图;pdegplot(模型,“EdgeLabels”,'上');轴([-。1.1 - 1。1 1.1]);标题“几何与边缘的标签显示”;
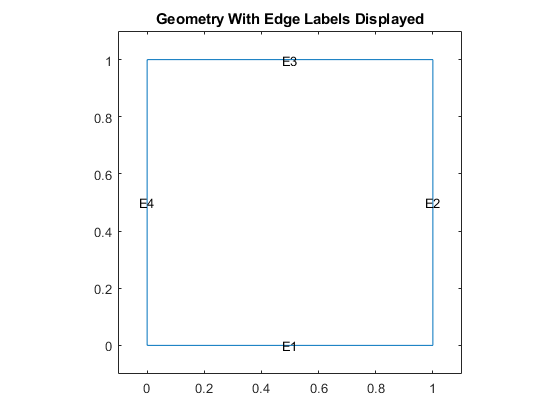
指定系数。通过将上面的方程与PDE工具箱文档中的标量抛物线方程进行比较,可以很容易地确定PDE工具箱所需系数的表达式。
C =厚* K;
因为辐射边界条件,在“a”系数是温度的函数,U。它被定义为一个MATLAB表达,因此它可以用于在分析过程中的u不同的值进行评价。
A = @(〜,状态)2 * hCoeff + 2 * * EMISS * stefanBoltz state.u ^ 3。F = 2 * * hCoeff TA + 2 * * EMISS * stefanBoltz TA ^ 4;d =厚* * RHO specificHeat;specifyCoefficients(模型,“米”,0,'d',0,'C'c'一个',一个,'F',F);
该板的底部边缘被设定为1000度开尔文。
应用边界条件。板的三个边是绝缘的。由于Neumann边界条件为0是有限元公式的默认值,这些边的边界条件不需要明确设置。在底边边1的所有节点上都设置了狄利克雷条件,
applyBoundaryCondition(模型,“狄氏”,'边缘',1'U',1000);
指定初始猜测。
setInitialConditions(型号,0);
在正方形上创建三角形网格,每个方向上大约有10个元素。
HMAX = 0.1;%的单元尺寸MSH = generateMesh(型号,“Hmax”,hmax);图;pdeplot(模型);轴等于标题“板三角形单元网格”xlabel“X坐标,米”ylabel“Y坐标,米”
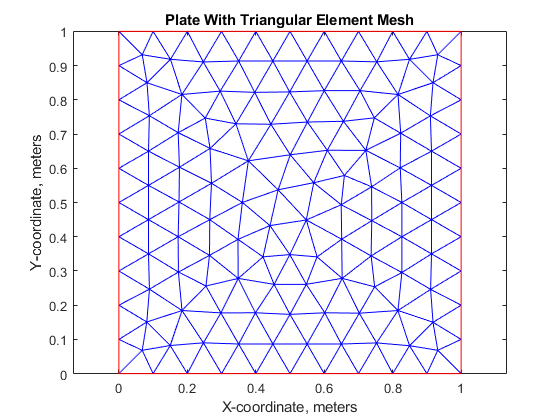
稳态解
由于A和F的系数是温度的函数(由于辐射边界条件),solvepde会自动选择非线性求解以获得溶液。
R = solvepde(模型);u = R.NodalSolution;图;pdeplot(模型,'XYData'u“轮廓”,'上',“ColorMap”,'喷射');标题“温中板,稳态解”xlabel“X坐标,米”ylabel“Y坐标,米”轴等于
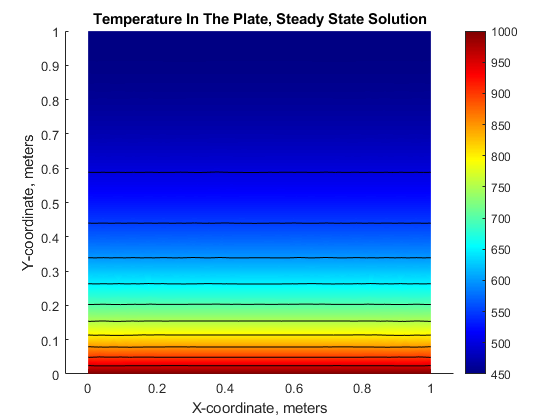
P = msh.Nodes;plotAlongY(P,U,0);标题“温度作为的函数的Y-座标”xlabel“Y坐标,米”ylabel“温度,度开尔文”
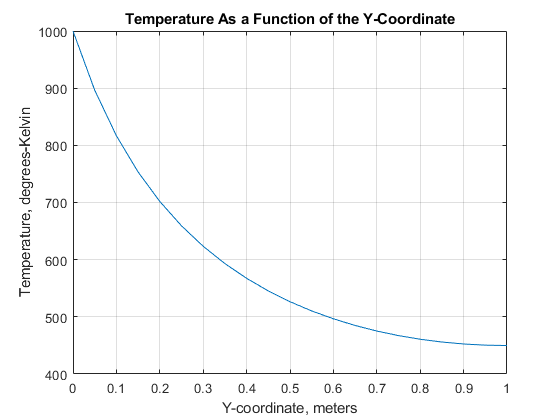
fprintf中(“在板的顶部边缘温度=%5.1f度-K \ N”,...U(4));
在板= 449.8度-K的顶部边缘温度
瞬态解
包括d系数。
specifyCoefficients(模型,“米”,0,'d'd'C'c'一个',一个,'F',F);ENDTIME = 5000;TLIST = 0:50:结束时间;numNodes =尺寸(P,2);
将所有节点的初始温度设置为ambient, 300k。
情况(1:numNodes) = 300;
在底边缘E1的初始温度设定为恒定BC的值,1000 K.
1000年setInitialConditions(模型,'边缘'1);
设置以下求解选项。
model.SolverOptions.RelativeTolerance = 1.0E-3;model.SolverOptions.AbsoluteTolerance = 1.0E-4;
通过解决问题solvepde。求解器自动选择抛物面求解器以获得溶液。
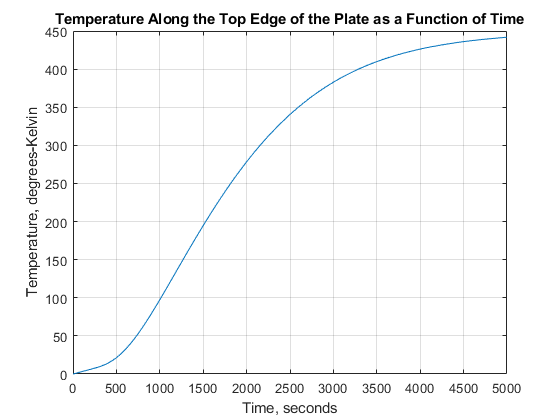
R = solvepde(型号,TLIST);u = R.NodalSolution;图;图(TLIST,U(3,:));格在标题"沿着板块顶部边缘的温度是时间的函数"xlabel“时间,秒”ylabel“温度,度开尔文”
图;pdeplot(模型,'XYData'中,u(:,端),“轮廓”,'上',“ColorMap”,'喷射');标题(sprintf的(“温度在板,瞬态解(%d秒)\ N”,...TLIST(1,端)));xlabel“X坐标,米”ylabel“Y坐标,米”轴等于;
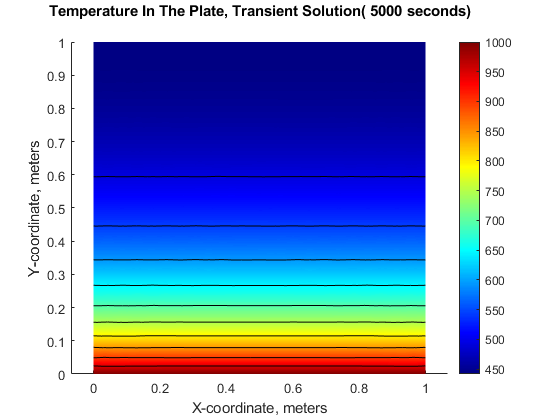
fprintf中('\nTemperature at the top edge(t=%5.1f秒)=%5.1f degrees-K\n',...tlist(结束),u (4));
顶部边缘温度(t=5000.0秒)=441.8度- k
总结
从稳态解到终态解,极板内的温度曲线非常接近。也就是说,在5000秒左右,瞬态解达到稳态值。两个溶液在盘子顶部边缘的温度一致在1%以内。金宝搏官方网站

