具有温度依赖性的传热问题
这个例子说明了如何解决热方程与温度有关的导热系数。算例给出了一个中心为矩形腔体的矩形块体的理想热分析。
瞬态导热的偏微分方程为:
哪里 是温度, 为材料密度, 是比热,和 是导热系数。 是物体内部产生的热量,在这个例子中是零。
稳态解决方案:恒定热导率
创建一个稳态热模型。
thermalmodelS=createpde(“热的”,“稳态”);
通过绘制一个块大小的矩形和另一个插槽大小的矩形来创建二维几何图形。
r1=[34-.5.5-.5-.8-.8.8];r2=[34-.05.05.05-.05-.4-.4.4];gdm=[r1;r2]';
从第一个矩形中减去第二个矩形以创建带有槽的块。
g=decsg(gdm,“R1-R2”, (“R1”;“R2”]“);
将decsg格式转换为一个几何对象。在模型中包含几何图形。
geometryFromEdges (thermalmodelS g);
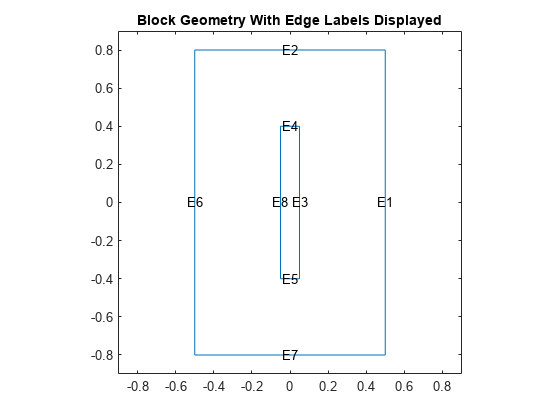
用显示的边标签打印几何图形。下面将在定义边界条件的函数中使用边标签。
图pdegplot (thermalmodelS,“EdgeLabels”,“开”);轴线([-.9 .9 -.9 .9]); title“显示边标签的块几何图形”
将左边边缘的温度设置为100度。在右边的边缘,有一个规定的热通量出块。顶部和底部的边缘和腔内的边缘都是绝缘的,也就是说,没有热量通过这些边缘传递。
thermalBC (thermalmodelS“边缘”6“温度”,100);thermalBC(thermalmodelS,“边缘”,1,“HeatFlux”, -10);
注明材料的导热系数。首先,考虑恒定的导热系数,例如,等于1。之后,考虑一个热导率是温度函数的情况。
thermalProperties (thermalmodelS“导热性”1);
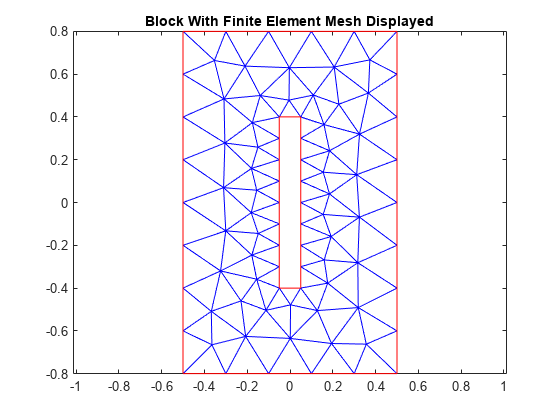
创建元素不大于0.2的网格。
generateMesh(热模型,“Hmax”, 0.2);图pdeplot (thermalmodelS);轴相同的标题“显示有限元网格的块体”
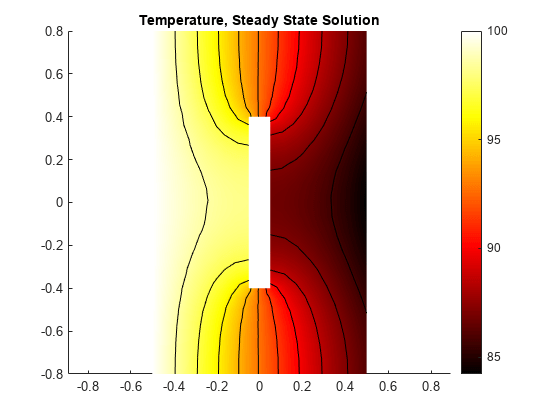
计算稳态解。
R=求解(热模型);T=R.温度;图pdeplot(热模型,“XYData”T“轮廓”,“开”,“ColorMap”,“热”);轴线相同的标题“温度,稳态溶液”
瞬态解决方案:恒定热导率
创建一个瞬态热模型,包括几何形状。
thermalmodelT=createpde(“热的”,“暂时的”);r1=[34-.5.5-.5-.8-.8.8];r2=[34-.05.05.05-.05-.4-.4.4];gdm=[r1;r2]';g=decsg(gdm,“R1-R2”, (“R1”;“R2”]“);geometryFromEdges (thermalmodelT g);
指定材料的导热系数、质量密度和比热。
thermalProperties (thermalmodelT“导热性”,1,...“质量密度”,1,...“SpecificHeat”1);
定义边界条件。在瞬时情况下,在时间=0时,左边缘的温度为零,并在0.5秒内上升到100度。您可以找到helper函数transientBCHeatedBlock在下面matlab/R20XXx/examples/pde/main.
thermalBC (thermalmodelT“边缘”6“温度”, @transientBCHeatedBlock);
在右边缘,有一个规定的热流出块。
thermalBC (thermalmodelT“边缘”,1,“HeatFlux”, -10);
顶部和底部的边缘以及腔内的边缘都是绝缘的,没有热量通过这些边缘传递。
创建元素不大于0.2的网格。
msh=生成网格(ThermalModel,“Hmax”,0.2);图pdeplot(ThermalModel);轴相同的标题“显示有限元网格的块体”
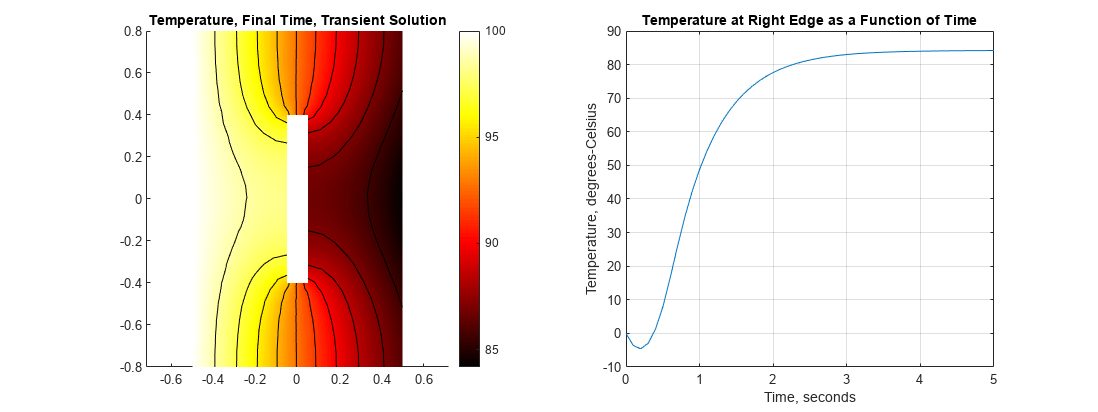
计算瞬态解。从0秒到5秒执行瞬态分析。工具箱每0.1秒保存一次解,以便创建随时间变化的结果图。
tlist = 0: .1:5;thermalIC(ThermalModel,0);R=求解(ThermalModel,tlist);T=R.温度;
两张图有助于理解这种瞬态分析的结果。第一个是最后时刻的温度图。第二张图显示的是街区中某一点的温度,在这个例子中是靠近右边缘的中心,它是时间的函数。为了识别靠近右边缘中心的节点,可以方便地定义这个简短的实用函数。
getClosestNode = @ (p, x, y)最小值((p (1:) - x)。^ 2 + (p (2:) - y)。^ 2);
调用此函数以获取右边缘中心附近的节点。
[~,nid] = getClosestNode(msh. exe, msh. exe);节点,.5,0);
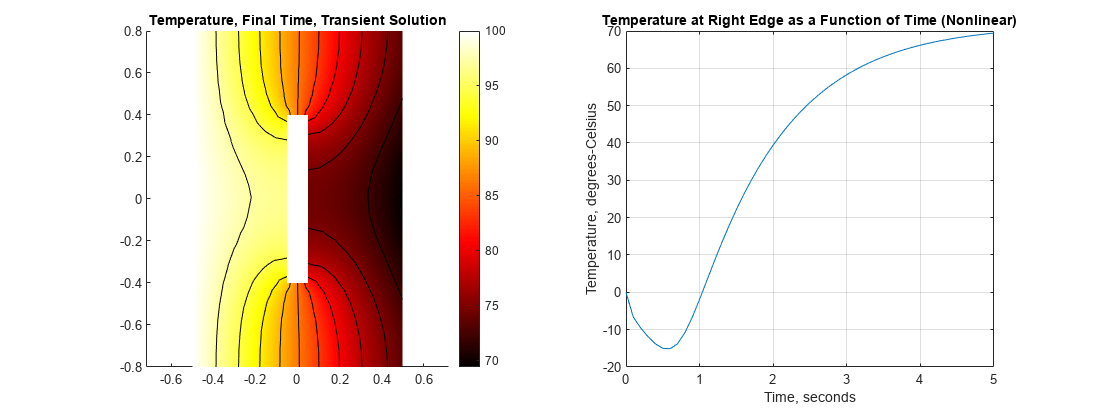
下图中并排显示了两个曲线图。此时的温度分布与从上述稳态溶液中获得的温度分布非常相似。在右边缘,在大约不到半秒的时间内,温度小于零。这是因为热量离开砌块的速度快于从lef到达砌块的速度当温度超过3秒时,温度基本上达到了稳定状态。
h=图形;h.位置=[1 2 1].*h.位置;子批次(1,2,1);轴相同的pdeplot (thermalmodelT“XYData”,T(:,结束),“轮廓”,“开”,“ColorMap”,“热”);轴线相同的标题‘温度、最终时间、瞬态溶液’次要情节(1、2、2);轴相同的,情节(tlist T(国家免疫日:));网格在标题“右边缘温度随时间变化”;包含“时间,秒”伊拉贝尔“温度,摄氏度”
稳态解决方案:温度依赖的导热系数
物质属性是因变量的函数是很常见的。例如,假设导热系数是温度的简单线性函数:
k=@(~,state)0.3+0.003*state.u;
在这种情况下,变量u是温度。在这个例子中,假设密度和比热不是温度的函数。
thermalProperties (thermalmodelS“导热性”、k);
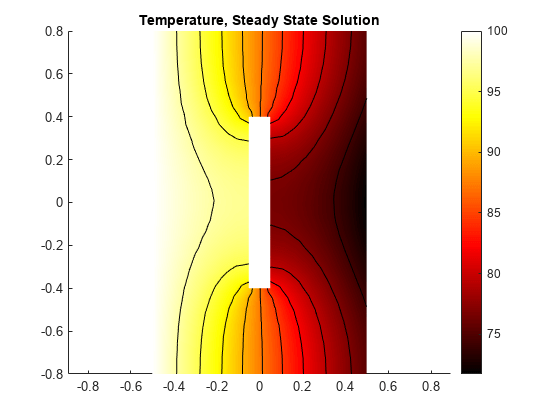
计算稳态解。与电导率恒定的情况相比,右边边缘的温度较低。这是由于温度较低的区域的电导率较低。
R=求解(热模型);T=R.温度;图pdeplot(热模型,“XYData”T“轮廓”,“开”,“ColorMap”,“热”);轴线相同的标题“温度,稳态溶液”
瞬态溶液:温度相关导热系数
现在用温度相关的电导率进行瞬态分析。
thermalProperties (thermalmodelT“导热性”K...“质量密度”,1,...“SpecificHeat”1);
使用相同的时间跨度tlist = 0: .1:5对于线性情况。
thermalIC(ThermalModel,0);R=求解(ThermalModel,tlist);T=R.温度;
绘制最后一个时间步的温度和右边缘的温度随时间变化的曲线图。最后一个时间步的温度曲线图与线性分析的可比曲线图仅略有不同:右边缘的温度略低于线性情况。温度随时间变化的曲线图为与线性情况大不相同。由于较低温度下的电导率较低,热量到达块体右边缘所需的时间较长。在线性情况下,温度在大约3秒时基本恒定,但对于这种非线性情况,温度曲线在5秒时才开始变平。
h=图形;h.位置=[1 2 1].*h.位置;子批次(1,2,1);轴相同的pdeplot (thermalmodelT“XYData”,T(:,结束),“轮廓”,“开”,“ColorMap”,“热”);轴线相同的标题‘温度、最终时间、瞬态溶液’次要情节(1、2、2);轴相同的情节(tlist(1:尺寸(T, 2))、T (nid:));网格在标题“右边缘温度与时间的函数(非线性)”;包含“时间,秒”伊拉贝尔“温度,摄氏度”