概述

图1:一个球从10米的高度以15米/秒的速度抛上来。

弹跳球模型是一个典型的例子混合动态系统．一个混合动态系统是一个系统，既包括连续的动态，也包括离散的转换，其中系统的动态可以改变，状态值可以跳跃。一个弹跳球的连续动力学简单地给出如下:

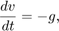
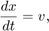
在哪里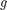为重力加速度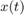，是球的位置和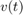是速度。因此，系统有两种连续状态:位置和速度．

该模型的混合系统方面源于对球与地面碰撞的建模。如果假设与地面的碰撞是部分弹性的，那么碰撞前的速度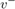，，以及碰撞后的速度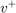，，可以用球的恢复系数联系起来，,如下所示:

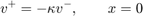
因此，弹跳球在过渡条件下显示一个连续状态(速度)的跳跃，．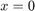

弹跳球是最简单的模型之一芝诺的现象．对于某些混合系统，芝诺行为被非正式地描述为在有限的时间间隔内发生无限个事件。当球在弹跳球模型中失去能量时，大量与地面的碰撞开始在连续较小的时间间隔内发生。因此模型经历了芝诺行为。模型与芝诺的行为在计算机上进行模拟固有的困难，但在许多常见和重要的工程应用中遇到。

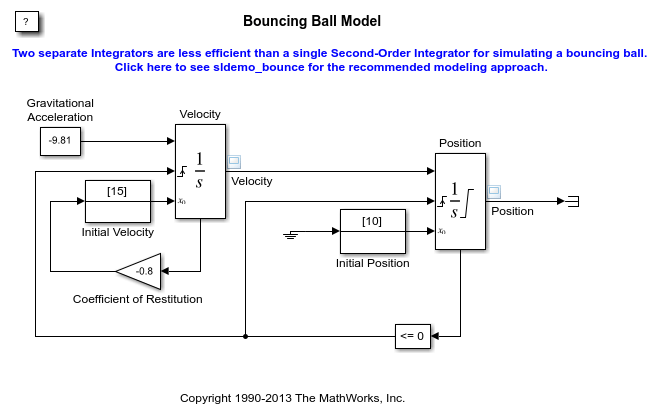
使用两个积分器块来模拟一个弹跳球

打开这个模型

您可以使用两个Integrator模块来建模一个弹跳球。左边的积分器是对第一个方程建模的速度积分器，右边的积分器是位置积分器。导航到位置积分器块对话框，观察它的下限为零。这个条件表示球不能进入地下的约束条件。

利用位置积分器的状态端口和相应的比较结果来检测球何时触地并复位两个积分器。利用速度积分器的状态端口进行计算．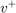

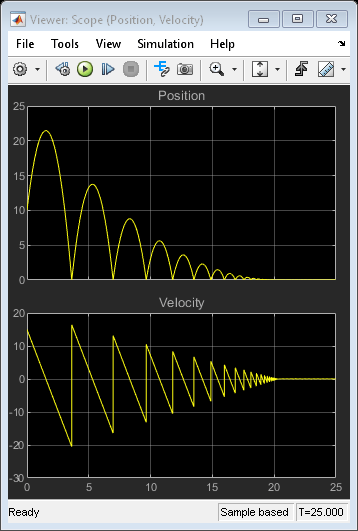
要观察系统的Zeno行为，导航到“配置参数”对话框的“求解器”窗格。在“过零选项”部分，确认“算法”设置为“非自适应”，模拟“停止时间”设置为25秒。运行仿真。

观察，当球越来越频繁地撞击地面并失去能量时，模拟误差会出现。因此，模拟超过了允许的“连续零交叉数”的默认限制1000。现在导航到配置参数对话框。在“过零选项”部分，将“算法”设置为“自适应”。该算法引入了一种复杂的处理这种抖振行为的方法。因此，您现在可以模拟超过20秒的系统。然而，请注意，状态在21秒到25秒之间的抖动和Simulink关于模型在20秒左右的强烈抖动的警告。金宝app

使用二阶积分器块来模拟弹跳球

打开这个模型

您可以使用单个的二阶积分器块来建模这个系统。第二个方程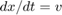在本例中是二阶积分器块的内部。导航到second order Integrator块对话框，并注意到，如前面所述，它的下限是0。导航到块对话框的属性选项卡，注意选项“当x达到饱和时重新初始化dx/dt”被选中。这个参数允许我们重新初始化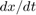（在弹跳球模型中)到一个新的值达到饱和极限。对于弹跳球模型，这个选项意味着当球撞击地面时，它的速度可以设置为一个不同的值，即撞击后的速度。注意计算与地面碰撞后的速度的循环。来捕捉速度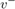球在碰撞前的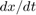使用二阶积分器块和内存块的输出端口。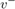然后用来计算反弹速度．

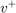导航到“配置参数”对话框的“求解器”窗格。确认“过零选项”部分的“算法”设置为“非自适应”，模拟“停止时间”设置为25秒。模拟模型。注意，模拟没有遇到任何问题。你能够在t = 20秒后模拟模型，而不会经历过多的抖动，也不会将“算法”设置为“自适应”。

二阶积分器模型是对弹跳球进行建模的较好方法

人们可以通过分析计算出确切的时间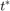当球以零速度降落到地面时，通过计算每次弹跳所需的时间。这个时间是一个无限几何级数的和:

在这里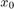和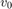分别为位置和速度的初始条件。球的速度和位置必须等于零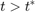．在下图中，两个模拟的结果被绘制在附近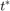．图中垂直的红线是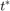为给定的模型参数。为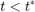远离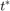在美国，两种模型得出的结果都是准确而相同的。因此，在图中只能看到第二个模型中的一条品红线。然而，后一种模型的仿真结果并不准确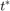；它继续表现出过度的喋喋不休的行为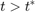．相比之下，使用二阶积分器块的第二个模型正好为零．

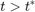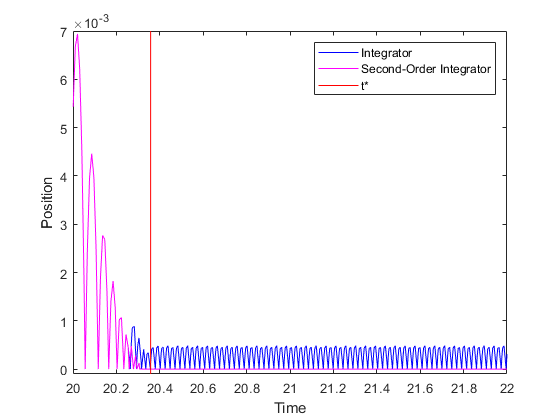
图2:比较两种方法的仿真结果。

从图2可以明显看出，第二种模型比第一种模型具有更好的数值特性。二阶积分器模型精度较高的原因如下。第二个微分方程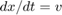是二阶积分器块的内部。因此，块算法可以利用这两种状态之间的已知关系，并部署启发式来抑制特定条件下不希望出现的聊天行为。当这两种状态由于集成错误和抖动行为而不再相互一致时，这些启发式就会变得活跃起来。因此，您可以使用系统的物理知识来缓解某些Zeno模型类的模拟陷入Zeno状态的问题。