因素分析模型

在因子分析模型中，测量变量取决于较少数量的未观察（潜在）因子。因为每个因素可能共同影响几个变量，所以它们被称为“共同因素”。假设每个变量取决于公因子的线性组合，系数称为载荷。每个测量变量还包括一个因独立随机变化而产生的分量，称为“特定方差”，因为它特定于一个变量。

具体来说，因素分析假设数据的协方差矩阵是这样的形式

SigmaX = * +

其中是载荷矩阵，对角矩阵的元素是具体的方差。这个函数法特朗使用最大似然拟合因子分析模型。

例如:寻找影响考试成绩的共同因素

120名学生每人参加五次考试，前两次涉及数学，后两次涉及文学，第五次是综合考试。对于一个学生来说，五个等级之间应该有联系，这似乎是合理的。有些学生两门都擅长，有些学生只擅长一门，等等。这一分析的目的是确定是否有定量证据表明，学生在五种不同考试中的成绩在很大程度上取决于两种能力。

首先加载数据，然后调用法特朗并请求一个带有单个公共因子的模型。

负载examgrades[Loadings1，specVar1，T，stats]=系数（等级，1）；

法特朗的前两个返回参数是估计的装载量和估计的特定方差。从估计的负荷中，你可以看到这个模型中的一个共同因素在所有五个变量上都有很大的正权重，但大多数权重在第五次综合考试上。

Loadings1

Loadings1 = 0.6021 0.6686 0.7704 0.7204 0.9153

对这种契合的一种解释是，人们可能会根据学生的“综合能力”来考虑他们，对此，综合考试将是最好的衡量标准。学生在特定学科的测试中所取得的成绩不仅取决于他们的综合能力，还取决于该学生在该领域是否优秀。这就解释了前四门考试的低负荷。

从估计的具体差异中，您可以看到该模型表明特定学生在特定测试中的分数变化很大，超出了由于共同因素造成的变化。

specVar1

specVar1 = 0.6375 0.5530 0.4065 0.4810 0.1623

一个特定的方差为1表示存在不该变量的公因子分量，而特定方差为0则表示该变量为完全由公共因素决定。这些考试成绩似乎介于两者之间，尽管综合考试的具体变化最小。这与上述对该模型中单一公共因素的解释是一致的。

函数中返回的p值统计数据结构拒绝了单一公因式的原假设，因此我们重新构建了模型。

stats.p

ans = 0.0332

接下来，使用两个常见因素来更好地解释考试成绩。使用不止一个因素，您可以旋转估计的载荷，以尝试简化其解释，但目前，请寻求一个未旋转的解决方案。

[Loadings2 specVar2 T,统计]= factoran(等级2“旋转”，“没有”）;

从估计的载荷中，您可以看到第一个未旋转因子对所有五个变量的权重大致相等，而第二个因子将前两个变量与后两个变量进行对比。

Loadings2

Loadings2 = 0.6289 0.3485 0.6992 0.3287 0.7785 -0.2069 0.7246 -0.2070 0.8963 -0.0473

您可以将这些因素解释为“整体能力”和“定量与定性能力”，扩展了先前对单因素拟合的解释。

变量的绘图(其中每个加载都是相应因素轴上的坐标)图形化地说明了这种解释。前两种考试对第二种因素有积极的影响，表明它们依赖于“定量”能力，而后两种考试显然依赖于相反的能力。第五次考试对第二个因素的影响很小。

biplot (Loadings2“varlabels”num2str ((1:5) '));标题(不旋转的解决方案的）;包含(“潜在因素1”）;ylabel (《潜在因素2》）;

从估计的特定方差中，你可以看到，这个双因素模型表明，由于公共因素，比单因素模型的变化更少。同样，第五次考试的特定差异最小。

specVar2

specVar2=0.4829 0.4031 0.3512 0.4321 0.1944

的统计数据结构表明，该双因素模型只有一个自由度。

stats.dfe

ans = 1

由于只有五个测量变量，您无法拟合包含两个以上因子的模型。

来自协方差/相关矩阵的因素分析

您可以使用原始测试分数进行上述匹配，但有时您可能只有一个总结数据的样本协方差矩阵。法特朗使用“Xtype”参数，并给出与原始数据相同的结果。

σ= x(成绩);[LoadingsCov, specVarCov] =.．.factoran(σ2“Xtype”，“浸”，“旋转”，“没有”)；装载

载荷COV=0.6289 0.3485 0.6992 0.3287 0.7785-0.2069 0.7246-0.2070 0 0.8963-0.0473

因子旋转

有时，因子分析模型中的估计负荷可能会对某些测量变量的多个因子赋予很大的权重，从而难以解释这些因子所代表的内容。因子旋转的目标是找到每个变量只有少量大负荷的解决方案，即受smal影响的解决方案l因素数量，最好只有一个。

如果将载荷矩阵的每一行视为M维空间中某个点的坐标，则每个因子对应一个坐标轴。因子旋转相当于旋转这些轴，并在旋转的坐标系中计算新的载荷。有多种方法可以做到这一点。有些方法使轴保持正交，而另一些方法是改变轴之间角度的倾斜方法。

方差是正交旋转的一个常见判据。法特朗默认情况下执行varimax旋转，所以不需要显式地请求它。

[LoadingsVM, specVarVM rotationVM] = factoran(等级2);

快速检查返回的最大旋转矩阵法特朗确认它是正交的。Varimax实际上是旋转上图中的因子轴，但使它们保持直角。

rotationVM‘* rotationVM

Ans = 1.0000 -0.0000 -0.0000 1.0000

五个变量对旋转因子的双图显示了最大旋转的影响。

biplot (LoadingsVM“varlabels”num2str ((1:5) '));标题(“最大方差法解决方案”）;包含(“潜在因素1”）;ylabel (《潜在因素2》）;

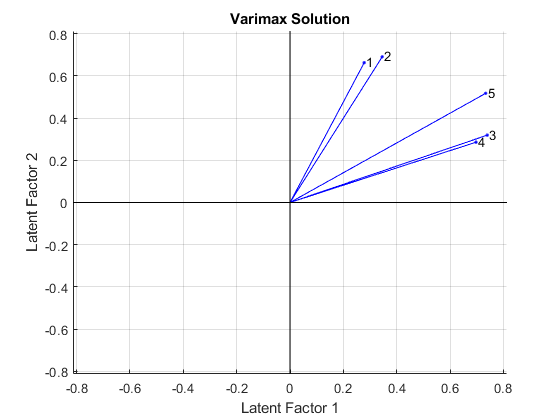
Varimax刚性旋转轴，试图使所有载荷接近零或一。前两种考试最接近第二因素轴，而第三和第四种考试最接近第一因素轴，第五种考试处于中间位置。这两个旋转的因素可以最好地解释为“定量能力”和“定性能力”。然而，由于没有一个变量靠近因子轴，双图显示正交旋转不能成功地提供一组简单的因子。

由于正交旋转不是完全令人满意的，您可以尝试使用promax，一种常见的斜旋转标准。

[LoadingsPM, specVarPM rotationPM] =.．.factoran（2级，“旋转”，“promax”）;

对返回的promax旋转矩阵进行检查法特朗这表明它不是正交的。实际上，Promax单独旋转第一个图形中的因子轴，使它们之间有一个斜角。

rotationPM‘* rotationPM

Ans = 1.9405 -1.3509 -1.3509 1.9405

新旋转因子上变量的双图显示了promax旋转的影响。

双批次（装载PM，“varlabels”num2str ((1:5) '));标题(“电子产品品牌解决方案”）;包含(“潜在因素1”）;ylabel (《潜在因素2》）;

Promax实现了轴的非刚性旋转，并且在创建“简单结构”方面比varimax做得更好。前两次考试接近第二个因素轴，第三次和第四次考试接近第一个因素轴，第五次考试处于中间位置。这使得将这些旋转的因素解释为“定量能力”和“定性能力”更加精确。

不是在不同的旋转轴上绘制变量，而是可以将旋转轴覆盖在一个未旋转的双图上，以更好地了解旋转和未旋转的解是如何关联的。金宝搏官方网站

h1 = biplot (Loadings2,“varlabels”num2str ((1:5) '));包含(“潜在因素1”）;ylabel (《潜在因素2》); 持有在…上invRotVM=inv（rotationVM）；h2=line（[-invRotVM（1,1）invRotVM（1,1）NaN-invRotVM（2,1）invRotVM（2,1）]，.．.[-invRotVM（1,2）invRotVM（1,2）NaN-invRotVM（2,2）invRotVM（2,2）]，以及，“颜色”，[10 0]）；invRotPM=inv（rotationPM）；h3=line（[-invRotPM（1,1）invRotPM（1,1）NaN-invRotPM（2,1）invRotPM（2,1）]，.．.[-invRotPM(1,2) invRotPM(1,2) NaN -invRotPM(2,2) invRotPM(1,2)]，“颜色”，[0 1 0]）；保持关轴广场lgndHandles=[h1（1）h1（结束）h2 h3]；lgndLabels={“变量”，不旋转的轴的，“方差极大旋转坐标轴”，“电子产品品牌旋转坐标轴”};传奇(lgndHandles lgndLabels,“位置”，“东北”，“字体名”，“arial窄”）;

预测因子得分

有时，能够根据观察结果的因子分数对其进行分类是很有用的。例如，如果您接受双因子模型和promax旋转因子的解释，您可能希望预测学生将来在数学考试中的表现。

由于数据是原始考试成绩，而不仅仅是它们的协方差矩阵，我们可以法特朗返回每个学生的两个旋转公共因子值的预测值。

(载荷、specVar旋转,统计,仅仅]=.．.factoran（2级，“旋转”，“promax”，“麦克斯特”, 200);biplot(载荷,“varlabels”num2str ((1:5) '),“分数”，preds）；头衔(“Promax解决方案的预测因子得分”）;包含(“文学能力”）;ylabel (“数学能力”）;

这张图显示了模型在原始变量(向量)和每个观测值(点)的预测分数方面的拟合。这种契合性表明，虽然一些学生在某一科目上表现很好，但在其他科目(第二和第四象限)上表现不佳，但大多数学生在数学和文学(第一和第三象限)上要么表现得很好，要么表现得很差。你可以通过观察这两个因素的估计相关矩阵来证实这一点。

发票(旋转的旋转*)

Ans = 1.0000 0.6962 0.6962 1.0000

因子分析与主成分分析的比较

主成分分析(PCA)和因子分析(FA)在术语和目标上有很多重叠。很多关于这两种方法的文献并没有区分它们，一些拟合FA模型的算法涉及到主成分分析。这两种方法都是降维技术，从某种意义上说，它们可以用一组较小的新变量来替换一组大的观测变量。他们也经常给出相似的结果。然而，这两种方法的目标和底层模型是不同的。粗略地说，当您仅仅需要使用更少的维度来总结或近似您的数据时(例如，可视化它)，您应该使用PCA;当您需要一个解释数据之间相关性的模型时，您应该使用FA。