依赖模拟输入之间

一个设计决策的蒙特卡罗模拟的是随机输入概率分布的选择。选择为每个变量的分布往往是简单的，但是决定什么应该依赖输入之间存在的可能不大。理想情况下，输入数据到仿真应反映了已知的实际数量建模之间的依赖。然而，可能存在以此为基础的模拟的任何依赖很少或没有信息，并且在这样的情况下，这是一个好主意，试验不同的可能性，以便确定该模型的灵敏度。

然而，可能难以实际生成与依赖随机输入时，它们具有不从标准多元分布分布。此外，一些标准的多变量分布的可以模拟只有非常有限的类型的依赖。它总是能够使得输入独立，虽然这是一个简单的选择，它并不总是合理的，并可能导致错误的结论。

例如，金融风险蒙特卡罗模拟可能有代表的保险损失不同来源的随机输入。这些输入可以建模为对数正态分布随机变量。一个合理的问题要问的是这两个输入之间的关系是如何影响模拟的结果。事实上，它可能来自相同的随机条件影响这两个来源的真实数据是已知的，而忽略了在模拟可能会导致错误的结论。

独立对数正态随机变量的模拟是琐碎的。最简单的方法是使用lognrnd功能。在这里，我们将使用mvnrnd函数生成N对独立正常的随机变量，然后exponentiate他们。注意，这里使用的协方差矩阵是对角的，即，Z的列之间的独立性

n = 1000;标准差= 0.5;。SigmaInd =西格玛^ 2 * [1 0。0 1]

SigmaInd = 0.2500 0 0 0.2500

ZInd = mvnrnd（[0 0]，SigmaInd，N）;XIND = EXP（ZInd）;情节（XIND（：，1），XIND（：，2），'');轴等于;轴（[0 5 0 5]）;xlabel（'X1');ylabel（'X2');

相关二元对数正态分布R.V.的也很容易产生，使用协方差矩阵具有非零非对角线项。

ρ= 7;SigmaDep =σ。^2 .* [1]ρ1]

SigmaDep = 0.2500 0.1750 0.1750 0.2500

ZDep = mvnrnd([0 0]， SigmaDep, n);XDep = exp (ZDep);

第二散点图示出了这两个二元分布之间的差异。

情节（XDep（：，1），XDep（：，2），'');轴等于;轴（[0 5 0 5]）;xlabel（'X1');ylabel（'X2');

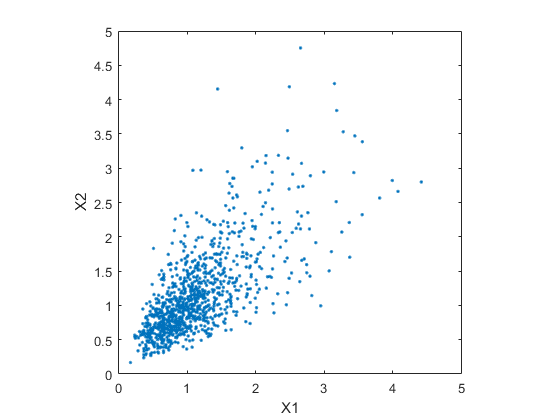
很明显，有更多的倾向的在第二数据集为要与为小的值X2的大的值，且类似地相关联的X1大的值。这种依赖性是由相关参数来确定，RHO底层二元正态的。从模拟中得出的结论可以很好取决于X1和X2是否用依赖或不产生。

二元数正态分布是在这种情况下一个简单的方案，当然容易推广到更高的尺寸和情况下边缘分布是不同lognormals。其它多元分布也存在，例如，多变量t和狄利克雷分布用于模拟依赖性T和β随机变量，分别。但简单的多变量分布的名单并不长，他们只在适用的情况下在边缘人都在同一个家庭（甚至是完全相同的分布）。这可以在许多情况下，一个真正的限制。

一种构造相关二元分布的更一般的方法

虽然创建一个对数正态分布二元上述结构很简单，它用于说明它是更普遍适用的方法。首先，我们生成二元正态分布值对。在这两个变量之间统计的依赖，每个人都有一个正常的边缘分布。接着，变换（指数函数）被单独地应用到每个变量，改变边缘分布成lognormals。转化的变量仍然有统计相关性。

如果一个合适的变换可以发现，这种方法可以推广到创建与其他边缘分布取决于二元随机向量。事实上，构建这种转化的一般方法确实存在，但不是那么简单，只是幂。

通过定义，在施加正常的CDF（由PHI这里表示）至标准正态随机变量导致R.V.即在区间[0，1]均匀。看到这一点，如果Z具有标准正态分布，则U = PHI（Z）的CDF是

镨【U <= U0} = PR {PHI（Z）<= U0} = PR {Z <= PHI ^（ -  1）（U0）} = U0，

那就是一个U（0,1）R.V.的CDF一些模拟正常和转化值的直方图证明这一事实。

n = 1000;z = normrnd (0, 1, n, 1);嘘(z, -3.75: .5:3.75);xlim ([4 4]);标题（“1000个模拟的N(0,1)随机值”);xlabel（“Z”);ylabel（'频率');

u = normcdf (z);嘘(u . 05。1: .95);标题（'转化到U（0,1）1000模拟N（0,1）的值');xlabel（'U');ylabel（'频率');

现在，从单变量的随机数生成的理论借用，在R.V.施加任何分布F的逆CDF到U（0,1）随机变量结果其分布正好F.这就是所谓的反演方法。证明基本上是前向的情况下在上述证明的相反。另一个直方图显示改造的伽玛分布。

x = gaminv (u 2 1);嘘(x,二十五分:.5:9.75);标题（'转化到伽玛（2,1）1000模拟N（0,1）的值');xlabel（“X”);ylabel（'频率');

这种两步变换可以应用到一个标准二元正态的每个变量，创建依赖R.V.的任意边缘分布。由于改造工程分别在每个部件上，两个结果R.V.的需求甚至没有相同的边际分布。该变换被定义为

Z = [Z1 Z2]〜N（[0 0]，[1个RHO; RHO 1]）U = [PHI（Z1）PHI（Z2）] X = [G1（U1）G2（U2）]

其中G1和G2是两种可能不同分布的逆CDFs。例如，我们可以从t(5)和(2,1)边值的二元分布中生成随机向量。

n = 1000;ρ= 7;Z = mvnrnd（[0 0]，[1个RHO;哌1]中，n）;U = normcdf（Z）;X = [gaminv（U（：，1），2,1）TINV（U（：，2），5）];

该地块具有直方图旁边的散点图显示两个边际分布，和依赖。

[N1，CTR1] = HIST（X（：，1），20）;[N2，CTR2] = HIST（X（：，2），20）;副区（2,2,2）;积（X（：，1），X（：，2），'');轴([0 12 -8 8]);甘氨胆酸h1 =;标题（“1000个模拟依赖性T和灰度值”);xlabel（“X1 ~γ(2,1)”);ylabel（'X2〜T（5）');次要情节(2、2、4);酒吧(ctr1 n1 1);轴（[0 12 -max（N1）* 1.1 0]）;轴（“关闭”);H2 = GCA;次要情节(2 2 1);BARH（CTR2，-n2,1）;轴（[ -  MAX（N 2）* 1.1 0 -8 8]）;轴（“关闭”);甘氨胆酸h3 =;h1。位置= [0.35 0.35 0.55 0.55];h2。位置= [。35 .1 .55 .15];h3。位置= [。1 .35 .15 .55]; colormap([.8 .8 1]);

秩相关系数

在这种结构中X1和X2之间的依赖性是由相关参数来确定，RHO底层二元正态的。但是，不X1和X2的线性相关是。例如，在原始的lognormal情况下，这种相关性有一个封闭的形式:

软木(X1, X2) = (exp(ρ*σ^ 2)- 1)。/ (exp(σ^ 2)- 1)

这比RHO严格少，除非RHO正好是一个。在更一般的情况下，虽然，如伽玛/吨以上结构，X1和X2之间的线性相关性是困难的或不可能在RHO的形式来表示，但模拟可以被用来表明，在相同的效果发生。

这是因为线性相关系数表示线性r.v之间的依赖。，当非线性变换应用于这些r.v时。，线性相关没有被保留。相反，排名相关系数(如Kendall’s tau或Spearman’s rho)更合适。

粗略地说，这些等级相关测量的程度一个R.V.的大或小的值与另一大或小的值相关联。然而，不同于线性相关系数，它们测量的关联仅在行列的条款。因此，排名的相关性在任何单调变换保留。具体地，刚刚描述的转化方法保留了等级相关。Therefore, knowing the rank correlation of the bivariate normal Z exactly determines the rank correlation of the final transformed r.v.'s X. While rho is still needed to parameterize the underlying bivariate normal, Kendall's tau or Spearman's rho are more useful in describing the dependence between r.v.'s, because they are invariant to the choice of marginal distribution.

事实证明，对二元正常，有Kendall的tau或Spearman的RHO，和线性相关系数RHO之间一个简单的一对一映射：

tau蛋白=（2 / PI）*反正弦（RHO）或RHO = SIN（TAU * pi / 2之间）rho_s =（6 / PI）*反正弦（RHO / 2）或哌= 2 * SIN（rho_s * PI / 6）

次要情节(1 1 1);ρ= 1:.01:1;τ= 2 * asin(ρ)。/π;rho_s = 6。* asin (rho. / 2)。/π;情节(ρ,τ,' - '，RHO，rho_s，' - '，[-1 1]，[ -  1 1]，凯西:”);轴([-1 -1 -1]);xlabel（'RHO');ylabel（“秩相关系数”);传说（“肯德尔的tau”，“斯皮尔曼的rho_s'，'位置'，'西北');

因此，可以很容易地创建X1和X2之间的期望等级相关，而不论其边缘分布的，通过选择Z1和Z2之间的线性相关的正确RHO参数值。

注意，对于多元正态分布，Spearman秩相关是几乎相同的线性关系。然而，一旦我们转换到最终的随机变量，这是不正确的。

Copula函数

上面描述的构造的第一步定义了所谓的联结，具体来说就是高斯联结。二元联结只是两个随机变量的概率分布，每个随机变量的边际分布是均匀的。这两个变量可能是完全独立的，确定相关的(例如，U2 = U1)，或者介于两者之间。二元高斯copulas族参数化为= [1];rho 1]，即线性相关矩阵。当趋向+/- 1时，U1和U2趋向于线性相关，当趋向于0时，它们趋向于完全独立。

对于各种级别的RHO说明的高斯连接函数不同的可能性的范围内的一些模拟随机值的散点图：

n = 500;Z = mvnrnd（[0 0]，[1 0.8; 0.8 1]中，n）;U = normcdf (Z, 0,1);次要情节(2 2 1);情节（U（：，1），U（：，2），'');标题（ρ= 0.8的);xlabel（'U1');ylabel（'U2');Z = mvnrnd（[0 0]，[1 0.1; 0.1 1]中，n）;U = normcdf (Z, 0,1);副区（2,2,2）;情节（U（：，1），U（：，2），'');标题（'RHO = 0.1');xlabel（'U1');ylabel（'U2');Z = mvnrnd([0 0]， [1 - 1;-。1,n);U = normcdf (Z, 0,1);次要情节(2、2、3);情节（U（：，1），U（：，2），'');标题（'RHO = -0.1');xlabel（'U1');ylabel（'U2');Z = mvnrnd（[0 0]，[1 -.8; -.8 1]中，n）;U = normcdf (Z, 0,1);次要情节(2、2、4);情节（U（：，1），U（：，2），'');标题（ρ= -0.8的);xlabel（'U1');ylabel（'U2');

U1和U2之间的依赖关系完全独立于X1 = G(U1)和X2 = G(U2)的边缘分布。X1和X2可以给出任何边缘分布，并且仍然具有相同的等级相关。这是Copula函数的主要诉求之一 - 它们允许依赖和边缘分布的这种单独的规范。

ŤCopula函数

从二元t分布出发，利用相应的t - CDF变换，可以构造出不同的交点族。二元t分布是参数化的与Rho，线性相关矩阵，和nu，自由度。因此，例如，我们可以说一个t(1)或一个t(5) copula，分别基于一个和五个自由度的多元t。

不同水平rho的一些模拟随机值的散点图说明了t(1)交点的不同可能性范围:

n = 500;ν= 1;T = mvtrnd([1 .8;.8 1]， nu, n);U = tcdf (T,ν);次要情节(2 2 1);情节（U（：，1），U（：，2），'');标题（ρ= 0.8的);xlabel（'U1');ylabel（'U2');T = mvtrnd（[1 0.1; 0.1 1]，NU，N）;U = tcdf (T,ν);副区（2,2,2）;情节（U（：，1），U（：，2），'');标题（'RHO = 0.1');xlabel（'U1');ylabel（'U2');T = mvtrnd（[1 -.1; -.1 1]，NU，N）;U = tcdf (T,ν);次要情节(2、2、3);情节（U（：，1），U（：，2），'');标题（'RHO = -0.1');xlabel（'U1');ylabel（'U2');T = mvtrnd([1 -.8;-。8 1]， nu, n);U = tcdf (T,ν);次要情节(2、2、4);情节（U（：，1），U（：，2），'');标题（ρ= -0.8的);xlabel（'U1');ylabel（'U2');

一件T Copula函数对U1和U2统一的边缘分布，就像高斯系词一样。在一吨系动词组件之间的等级相关的tau或rho_s也RHO作为高斯的相同的功能。然而，如这些图证明，一个T（1）的不同之连接函数相当多的从高斯连接函数，即使当它们的部件具有相同的等级相关。所不同的是他们依赖的结构。这并不奇怪，因为自由度参数NU的变大，叔（NU）连接函数接近高斯对应系动词。

作为具有高斯连接函数，任何边缘分布可以在吨系动词的罚款。例如，使用一吨系动词与1个自由度，我们可以再次从与邯（2,1）和t（5）边缘人一个二元分布生成随机向量：

次要情节(1 1 1);n = 1000;ρ= 7;ν= 1;T = mvtrnd（[1个RHO;哌1]，NU，N）;U = tcdf (T,ν);X = [gaminv（U（：，1），2,1）TINV（U（：，2），5）];[N1，CTR1] = HIST（X（：，1），20）;[N2，CTR2] = HIST（X（：，2），20）;副区（2,2,2）; plot(X(:,1),X(:,2),'');轴（[0 15 -10 10]）;甘氨胆酸h1 =;标题（“1000个模拟依赖性T和灰度值”);xlabel（“X1 ~γ(2,1)”);ylabel（'X2〜T（5）');次要情节(2、2、4);酒吧(ctr1 n1 1);轴（[0 15 -max（N1）* 1.1 0]）;轴（“关闭”);H2 = GCA;次要情节(2 2 1);BARH（CTR2，-n2,1）;轴（[ -  MAX（N 2）* 1.1 0 -10 10]）;轴（“关闭”);甘氨胆酸h3 =;h1。位置= [0.35 0.35 0.55 0.55];h2。位置= [。35 .1 .55 .15];h3。位置= [。1 .35 .15 .55]; colormap([.8 .8 1]);

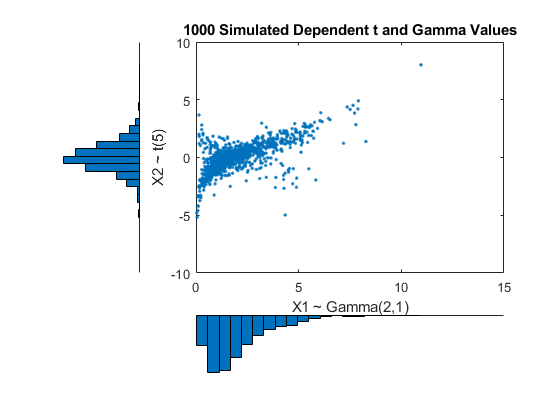
Compared to the bivariate Gamma/t distribution constructed earlier, which was based on a Gaussian copula, the distribution constructed here, based on a t(1) copula, has the same marginal distributions and the same rank correlation between variables, but a very different dependence structure. This illustrates the fact that multivariate distributions are not uniquely defined by their marginal distributions, or by their correlations. The choice of a particular copula in an application may be based on actual observed data, or different copulas may be used as a way of determining the sensitivity of simulation results to the input distribution.

高阶Copula函数

高斯和t交点称为椭圆交点。将椭圆交点推广到更高的维数是很容易的。例如，我们可以用(2,1)、(2,2)和t(5)边际的三变量分布模拟数据，使用高斯copula如下所示。

次要情节(1 1 1);n = 1000;的Rho = [1 0.4 0.2;0.4 1 -.8;0.2 -.8 1];Z = mvnrnd（[0 0 0]，ρ，N）;U = normcdf (Z, 0,1);X = [gaminv（U（：，1），2,1）BETAINV（U（：，2），2,2）TINV（U（：，3），5）];plot3（X（：，1），X（：，2），X（：，3），'');格上;视图（[ -  55，15]）;xlabel（'U1');ylabel（'U2');zlabel（'U3');

注意，和线性相关参数RHO之间的关系，例如，Kendall的tau，保持用于在所述相关矩阵的Rho这里使用的每个条目。我们可以验证该数据的样本等级相关近似等于理论值。

tauTheoretical = 2 * ASIN（RHO）./ PI

tauTheoretical = 1.0000 0.2620 0.1282 0.2620 1.0000 -0.5903 0.1282 -0.5903 1.0000

tauSample =科尔（X，“类型”，“肯德尔）

tauSample = 1.0000 0.2655 0.1060 0.2655 1.0000 -0.6076 0.1060 -0.6076 1.0000

Copula函数与实证边缘分布

要使用系词模拟相关多元数据，我们已经看到，我们需要指定

1）系动词家族（和任何形状参数），2）变量之间的相关性等级，以及3）每个变量的边缘分布

假设我们有两套股票收益数据，我们想运行蒙特卡罗模拟与遵循相同的分布作为数据输入。

加载stockreturnsNOBS =尺寸（股票，1）;副区（2,1,1）;HIST（股票（：，1），10）;xlabel（'X1');ylabel（'频率');副区（2,1,2）;HIST（股票（：，2），10）;xlabel（'X2');ylabel（'频率');

（这两个数据向量具有相同的长度，但是这不是关键的。）

我们可以分别拟合参数模型每个数据集，并使用这些估计我们的边际分布。然而，参数模型可能不够灵活。相反，我们可以采用一种经验模型的边缘分布。我们只需要一种方法来计算逆CDF。

对于这些数据集的实证逆CDF仅仅是一个阶梯函数，与在值1 / NOBS，2 / NOBS步骤，...... 1.阶梯高度简单地排序的数据。

invCDF1 =排序(股票(:1));n1 =长度(股票(:1));invCDF2 =排序(股票(:,2));n2 =长度(股票(:,2));次要情节(1 1 1);楼梯(invCDF1(1:脑袋)/脑袋,'B');持有上;楼梯（（1：NOBS）/ NOBS，invCDF2，'R');持有从;传说（'X1'，'X2');xlabel（“累计概率”);ylabel（“X”);

对于模拟，我们可能需要用不同的Copula函数和相关性进行试验。在这里，我们将使用一个二元T（5）系词有相当大的负相关参数。

n = 1000;RHO = -.8;NU = 5;T = mvtrnd（[1个RHO;哌1]，NU，N）;U = tcdf (T,ν);X = [invCDF1（小区（N1 * U（：，1）））invCDF2（小区（N 2 * U（：，2）））];[N1，CTR1] = HIST（X（：，1），10）;[N2，CTR2] = HIST（X（：，2），10）;副区（2,2,2）;积（X（：，1），X（：，2），'');轴（[ -  3.5 3.5 -3.5 3.5]）;甘氨胆酸h1 =;标题（“1000个模拟相关的值”);xlabel（'X1');ylabel（'X2');次要情节(2、2、4);酒吧(ctr1 n1 1);轴([-3.5 3.5 -max(n1)*1.1 0]);轴（“关闭”);H2 = GCA;次要情节(2 2 1);BARH（CTR2，-n2,1）;轴（[ -  MAX（N 2）* 1.1 0 -3.5 3.5]）;轴（“关闭”);甘氨胆酸h3 =;h1。位置= [0.35 0.35 0.55 0.55];h2。位置= [。35 .1 .55 .15];h3。位置= [。1 .35 .15 .55]; colormap([.8 .8 1]);

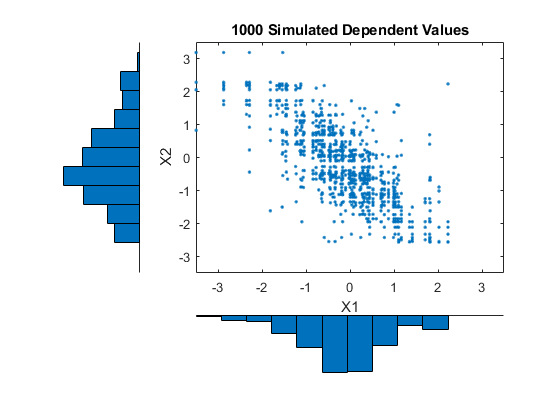
模拟数据的边际直方图紧密匹配的原始数据，并作为我们模拟更对值会变得相同。注意，值从原始数据绘制的，因为只有在100每个数据集意见中，模拟数据是有点“离散的”。要克服这一点的一种方法是加入少量随机变化的，可能是正态分布的，到最后的模拟值。这相当于使用经验逆CDF的平滑版本。