用累积概率拟合单变量分布

打开脚本

这个例子展示了如何使用累积分布函数的最小二乘估计来拟合单变量分布。这是一种普遍适用的方法，在最大可能性失败的情况下可能很有用，例如一些包含阈值参数的模型。

用数据拟合单变量分布最常用的方法是最大似然法。但是，最大似然法并非在所有情况下都适用，有时还需要其他估计方法，如矩量法。在适用的情况下，最大似然可能是更好的方法选择，因为它通常更有效。但是这里描述的方法提供了另一个工具，可以在需要时使用。

用最小二乘法拟合指数分布

术语“最小二乘”最常用于拟合一条回归线或曲面，将响应变量建模为一个或多个预测变量的函数。这里描述的方法是最小二乘的一个非常不同的应用:单变量分布拟合，只有一个变量。

首先，模拟一些示例数据。我们用指数分布来生成数据。对于本例的目的，在实践中，我们假设数据不知道来自某个特定的模型。

rng(37岁,“旋风”）;n = 100;x = exprnd (2 n 1);

接下来，计算数据的经验累积分布函数（ECDF）。这是一个简单的阶跃函数，在每个数据点x处累积概率p为1/n。

x=排序（x）；p=（（1:n）-0.5）./n；楼梯（x，p，“k -”）;包含(“x”）;ylabel (“累积概率(p)”）;

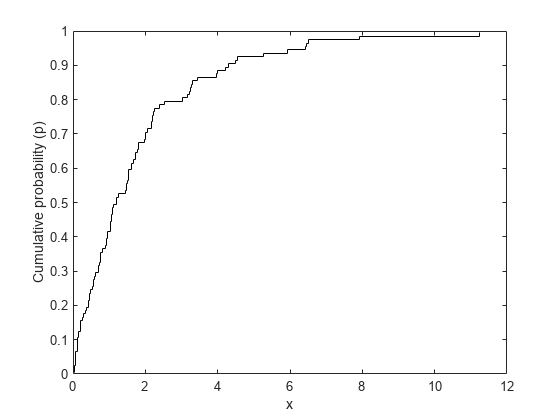
我们用指数分布来拟合这些数据。一种方法是找到其累积分布函数(CDF)与数据的ECDF最接近的指数分布(在某种意义上，将在下文解释)。指数CDF为p = Pr{X <= X} = 1 - exp(- X /mu)。将其转换为-log(1-p)*mu = x，得到-log(1-p)和x之间的线性关系。如果数据确实来自指数，我们应该看到，至少近似地，一个线性关系，如果我们将计算出的x和p值从ECDF代入那个方程。如果我们用最小二乘法拟合一条从原点到x的直线与-log(1-p)，那么这条拟合的直线表示的是最接近数据的指数分布。直线的斜率是mu参数的估计值。

同样，我们可以把y = -log(1-p)看作是来自标准(均值1)指数分布的“理想样本”。这些理想化的值在概率尺度上是完全等间距的。x和y的Q-Q曲线应该近似线性如果数据来自指数分布，我们用最小二乘线从原点到x / y。

Y = log(1 - p);muHat = y \ x

muHat=1.8627

绘制数据和拟合线。

图（x，y，“+”y * muHat y“r——”）;包含(“x”）;ylabel (“y =日志(1 - p)的）;

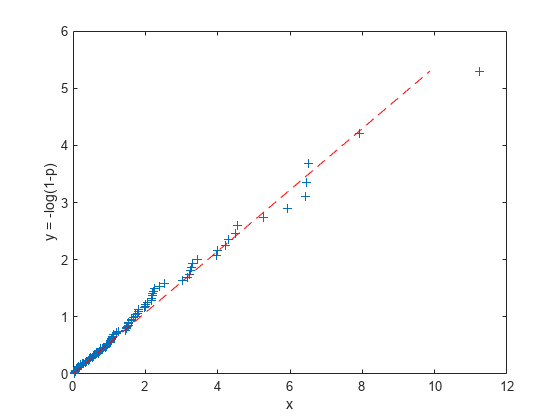
请注意，我们所做的线性拟合使水平方向或“x”方向上的平方误差之和最小化，这是因为y=-log（1-p）的值是确定性的，x值是随机的。也可以对y和x进行回归，或者使用其他类型的线性拟合，例如加权回归、正交回归，甚至稳健回归。我们在这里不探讨这些可能性。

为了比较，用最大似然拟合数据。

muMLE=expfit（x）

muMLE=1.7894

现在在未转换累积概率尺度上绘制两个估计分布。

楼梯(x, p,“k -”)；持有在xgrid=linspace（0,1.1*max（x），100）”；绘图（xgrid，expcdf（xgrid，muHat），“r——”，xgrid，expcdf（xgrid，muMLE），“b——”)；持有关包含(“x”）;ylabel (“累积概率(p)”）;传奇({“数据”，“LS配合”，毫升装的},“位置”，‘东南’）;

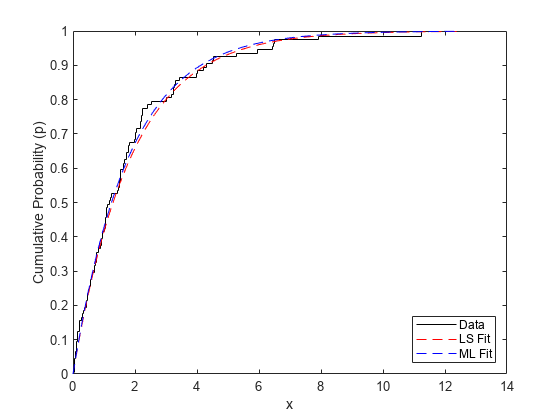
两种方法给出了非常相似的拟合分布，尽管LS拟合受分布尾部观测值的影响更大。

拟合威布尔分布

对于稍微复杂一点的示例，模拟来自Weibull分布的一些示例数据，并计算x的ECDF。

n = 100;x = wblrnd (2, 1, n, 1);x = (x);P = ((1:n)-0.5)' ./ n;

为了使威布尔分布适合这些数据，请注意，威布尔的CDF为p=Pr{X<=X}=1-exp（-X/a）^b）。将其转换为log（a）+log（-log（1-p））*（1/b）=log（X）再次给出了一个线性关系，这次是log（-log（1-p））和log（X）之间的关系.我们可以使用最小二乘法在转换后的比例尺上拟合一条直线，使用ECDF中的p和x，该直线的斜率和截距可得出a和b的估计值。

计算lnx =日志(x);= log(-log(1 - p));保利= polyfit(呆呆的计算lnx 1);paramHat = [exp(poly(2)) 1/poly(1)]

paramHat = 2.1420 1.0843

在转换后的比例尺上绘制数据和拟合线。

情节(计算lnx,呆呆的,“+”，log (paramHat(1)) + logy/paramHat(2)，“r——”）;包含(日志(x)的）;ylabel (日志(日志(1 - p))”）;

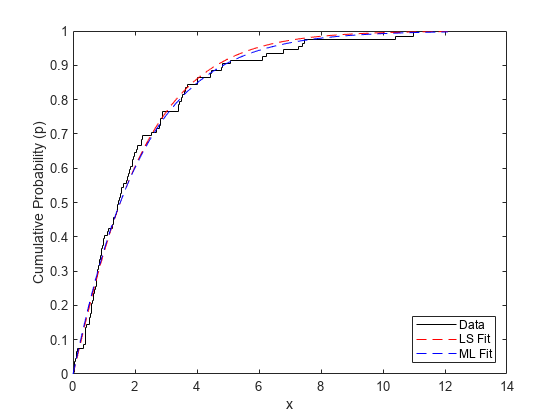
为了比较，用最大似然拟合数据，并在未转换尺度上绘制两个估计分布。

paramMLE = wblfit(x) stairs(x,p，“k”)；持有在xgrid = linspace (0, 1.1 * 100 (max (x)) ';情节(xgrid wblcdf (xgrid paramHat (1) paramHat (2)),“r——”，．..xgrid, wblcdf (xgrid paramMLE (1) paramMLE (2)),“b——”)；持有关包含(“x”）;ylabel (“累积概率(p)”）;传奇({“数据”，“LS配合”，毫升装的},“位置”，‘东南’）;

paramMLE = 2.1685 1.0372

阈值参数示例

有时需要用阈值参数来拟合正分布，如威布尔分布或对数正态分布。例如，Weibull随机变量的值超过(0,Inf)，而阈值参数c将该范围移动到(c,Inf)。如果阈值参数是已知的，那么就没有困难。但如果阈值参数未知，则必须对其进行估计。这些模型很难用最大可能性来拟合——可能性可能有多个模式，甚至可能因为对数据不合理的参数值而变得无限，所以最大可能性通常不是一个好方法。但只要对最小二乘法稍加补充，我们就能得到稳定的估计。

为了说明这一点，我们将用一个阈值来模拟三个参数的威布尔分布中的一些数据。如上所述，为了示例的目的，我们假设不知道数据来自特定模型，也不知道阈值。

n = 100;X = wblrnd(4,2,n,1) + 4;嘘(x, 20);xlim ([0 16]);

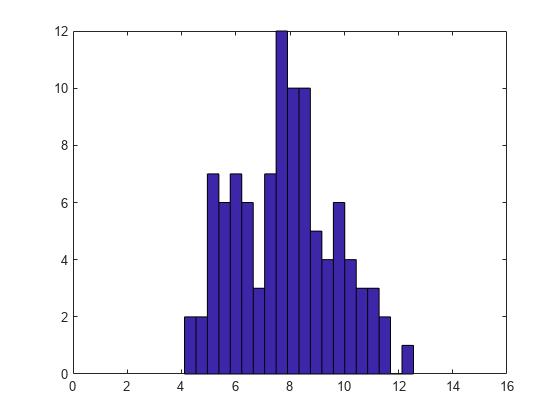
我们如何将三参数威布尔分布拟合到这些数据中？例如，如果我们知道阈值为1，我们可以从数据中减去该值，然后使用最小二乘法估计威布尔形状和比例参数。

x = (x);P = ((1:n)-0.5)' ./ n;呆呆的=日志(日志(1 - p));logxm1 =日志(x - 1);poly1 = polyfit(日志(日志(1 - p)),日志(x - 1), 1);paramHat1 = [exp(poly1(2)) 1/poly1(1)]“b +”，log（paramHat1（1））+logy/paramHat1（2），logy，“r——”）;包含('日志（x-1）'）;ylabel (日志(日志(1 - p))”）;

paramHat1 = 7.4305 4.5574

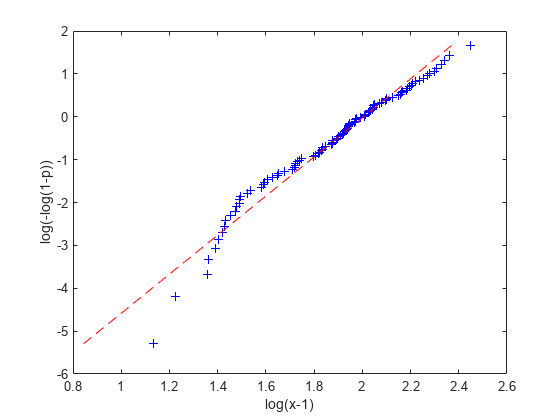
不是很吻合，log(x-1)和log(-log(1-p))不是线性关系。当然，这是因为我们不知道正确的阈值。如果我们尝试减去不同的阈值，我们得到不同的图和不同的参数估计。

logxm2=log（x-2）；poly2=polyfit（log（-log（1-p）），log（x-2），1）；paramHat2=[exp（poly2（2））1/poly2（1）]

paramHat2 = 6.4046 3.7690

logxm4 =日志(* 4);poly4 = polyfit(日志(日志(1 - p)),日志(* 4),1);paramHat4 = [exp(poly4(2)) 1/poly4(1)]

参数4=4.3530 1.9130

情节(logxm1,呆呆的,“b +”logxm2呆呆的,' r + 'logxm4呆呆的,g +的，．..日志(paramHat1(1)) +呆呆的/ paramHat1(2),呆呆的,“b——”，．..日志(paramHat2(1)) +呆呆的/ paramHat2(2),呆呆的,“r——”，．..日志(paramHat4(1)) +呆呆的/ paramHat4(2),呆呆的,“g——”）;包含(“日志(x - c)”）;ylabel (日志(日志(1 - p))”）;传奇({“阈值= 1”“阈值=2”“阈值= 4”},“位置”，“西北”）;

log(x-4)和log(-log(1-p))之间的关系近似成线性。由于我们期望看到一个近似线性的图，如果我们减去真正的阈值参数，这是4可能是阈值的一个合理值的证据。另一方面，2和3的图与线性图有更系统的不同，这证明这些值与数据不一致。

这个论点可以被形式化。对于阈值参数的每一个临时值，对应的临时威布尔拟合可以被描述为在变换变量log(x-c)和log(-log(1-p))上线性回归的R^2值最大化的参数值。为了估计阈值参数，我们可以更进一步，在所有可能的阈值上使R^2的值最大化。

r2 = @ (x, y) 1 -范数(y - polyval (polyfit (x, y, 1), x))。²/模(y -均值(y))²;threshObj = @(c) -r2(log(-log(1-p))，log(x-c));聊天= fminbnd (threshObj,炮*分钟(x) .9999 *分钟(x));保利= polyfit(日志(日志(1 - p)),日志(x-cHat), 1);paramHat = [exp(poly(2)) 1/poly(1) cHat] logx = log(x-cHat);呆呆的=日志(日志(1 - p));情节(计算lnx,呆呆的,“b +”，log (paramHat(1)) + logy/paramHat(2)，“r——”）;包含(的日志(x -聊天)）;ylabel (日志(日志(1 - p))”）;

paramHat = 4.7448 2.3839 3.6029

Non-Location-Scale家庭

指数分布是一个尺度族，而在对数尺度上，威布尔分布是一个位置尺度族，所以最小二乘法在这两种情况下是直接的。拟合位置-规模分布的一般程序是

计算观测数据的ECDF。
对分布的CDF进行变换，得到数据的某个函数与累积概率的某个函数之间的线性关系。这两个函数不涉及分布参数，但直线的斜率和截距涉及。
将ECDF中的x和p值代入转换后的CDF中，并使用最小二乘拟合一条直线。
根据直线的斜率和截距求解分布参数。

我们还看到，拟合一个带有附加阈值参数的位置-规模家庭分布只是稍微困难一点。

但是其他不以位置为尺度的家族分布，比如伽马，就有点棘手了。CDF的变换不会给出线性的关系。然而，我们可以使用类似的想法，只是这次工作在未转换的累积概率尺度。P-P图是将拟合过程形象化的合适方法。

如果将来自ECDF的经验概率与来自参数模型的拟合概率绘制在一起，沿着从0到1的1:1线的紧密散点表明，参数值定义了一种能够很好地解释观测数据的分布，因为拟合的CDF很好地逼近了经验CDF。其思想是找到使概率图尽可能接近1:1的参数值。如果分布不是一个很好的数据模型，这甚至可能是不可能的。如果P-P图显示出与1:1线的系统偏离，那么这个模型可能是有问题的。然而，重要的是要记住，由于这些图中的点不是独立的，解释与回归残差图并不完全相同。

例如，我们将模拟一些数据并拟合伽马分布。

n = 100;x = gamrnd (2, 1, n, 1);

计算x的ECDF。

x=排序（x）；pEmp=（（1:n）-0.5）./n；

我们可以使用任意gamma分布参数的初始猜测来绘制概率图，例如a=1和b=1。这个猜测不是很好——来自参数CDF的概率与来自ECDF的概率不太接近。如果我们尝试不同的a和b，我们会得到不同的散点在P-P图上，与1:1的线有不同的差异。因为在这个例子中我们知道了a和b的真实值，所以我们将尝试这些值。

a0 = 1;b0 = 1;p0Fit = gamcdf (x, a0, b0);a1 = 2;b1 = 1;p1Fit = gamcdf (x, a1, b1);情节([0,1],[0,1],“k——”pEmp p0Fit,“b +”pEmp p1Fit,' r + '）;包含(“经验概率”）;ylabel (“(临时)拟合伽玛概率”）;传奇({“1:1线”，“a = 1, b = 1”，“= 2,b = 1”},“位置”，‘东南’）;

第二组a和b的值有助于绘制更好的图，因此与数据更兼容，如果您是通过如何使P-P图直来衡量“兼容”的话。

为了使散点尽可能与1:1线匹配，我们可以找到a和b的值，使到1:1线的距离平方和的加权和最小化。权重是根据经验概率定义的，在图的中心是最低的，在极端是最高的。这些权重补偿了拟合概率的方差，在中位数附近的方差最高，在尾部的方差最低。这个加权最小二乘法定义了a和b的估计量。

wgt = 1 ./ sqrt(pmp .*(1- pmp));gammaObj = @ (params)和(重量。* (gamcdf (x, exp (params (1)), exp (params (2))) -pEmp)。^ 2);paramHat = fminsearch (gammaObj,日志(a1),日志(b1)]);paramHat = exp (paramHat)

参数=2.2759 0.9059

pFit = gamcdf (x, paramHat (1) paramHat (2));情节([0,1],[0,1],“k——”pEmp pFit,“b +”）;包含(“经验概率”）;ylabel (“安装伽马概率”）;

注意，在前面考虑的位置规模的情况下，我们可以用一条直线拟合分布。这里，与阈值参数示例一样，我们必须迭代地找到最适合的参数值。

模型规格错误

P-P图也可以用于比较来自不同分布族的拟合。如果这些数据符合对数正态分布会怎样呢?

wgt=1./sqrt（pEmp.*（1-pEmp））；LNobj=@（参数）总和（wgt.*（logncdf（x，参数（1），exp（参数（2）））-pEmp）。^2）；mu0=平均值（对数（x））；sigma0=std（log（x））；paramHatLN=fminsearch（LNobj[mu0，log（sigma0）]）；paramHatLN（2）=exp（paramHatLN（2））

paramHatLN = 0.5331 0.7038

pFitLN = logncdf (x, paramHatLN (1) paramHatLN (2));持有在地块（pEmp、pFitLN、，“rx”)；持有关ylabel (“拟合概率”）;传奇({“1:1线”，“安装伽马”，“拟合对数正态分布”},“位置”，‘东南’）;

注意对数正态拟合与尾部的γ拟合在系统上是如何不同的。左尾巴长得更慢，右尾巴死得更慢。伽马似乎更符合数据。

对数正态阈值参数示例

对数正态分布很容易用最大似然来拟合，因为一旦对数据进行对数变换，最大似然就等同于拟合一个正态分布。但在对数正态模型中，有时需要估计一个阈值参数。这种模型的可能性是无界的，因此最大可能性是不可行的。然而，最小二乘法提供了一种估算方法。由于双参数对数正态分布可以通过对数转换为位置-规模的族，因此我们可以按照前面示例中的步骤，使用阈值参数拟合威布尔分布。然而，在这里，我们将在累积概率尺度上进行估计，就像在前面的例子中显示的与伽马分布的拟合一样。

为了举例说明，我们将模拟一些来自三参数对数正态分布的数据，带有一个阈值。

n=200；x=lognrnd（0.5，n，1）+10；hist（x，20）；xlim（[8 15]）；

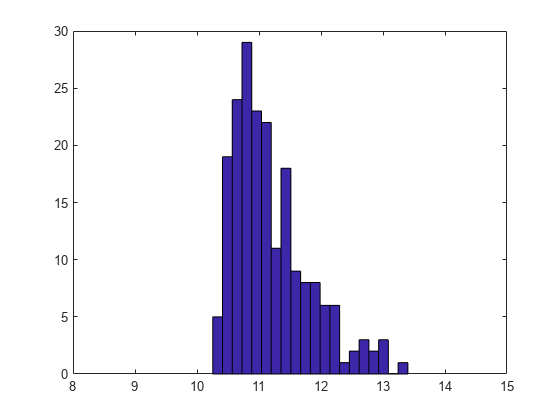
计算x的ECDF，并找出最佳拟合三参数对数正态分布的参数。

x=排序（x）；pEmp=（（1:n）-0.5）./n；wgt = 1 ./ sqrt(pmp .*(1- pmp));LN3obj = @ (params)和(重量。* (logncdf (x-params(3),参数个数(1),exp (params (2))) -pEmp)。^ 2);c0 = 0 *分钟(x);mu0 =意味着(日志(x-c0));sigma0 =性病(日志(x-c0));paramHat = fminsearch (LN3obj [mu0日志(sigma0), c0]);paramHat (2) = exp (paramHat (2))

参数=-0.0698 0.5930 10.1045

pFit = logncdf (x-paramHat (3), paramHat (1) paramHat (2));情节(pEmp pFit,“b +”，[0 1]，[0 1]，“k——”）;包含(“经验概率”）;ylabel (“拟合3参数对数正态概率”）;

精度的措施

参数估计只是问题的一部分——模型匹配还需要测量估计的精确度，通常是标准误差。在极大似然条件下，通常的方法是利用信息矩阵和大样本渐近参数来近似重复抽样下估计器的协方差矩阵。对于这些最小二乘估计量不存在这样的理论。

然而，蒙特卡罗模拟提供了另一种估计标准误差的方法。如果我们使用拟合模型生成大量数据集，我们可以用蒙特卡罗标准差近似估计量的标准误差。为简单起见，我们在单独的文件中定义了一个拟合函数，logn3fit.m．

estsSim=零（1000,3）；为i = 1:size(estsSim,1) xSim = logrnd (paramHat(1)，paramHat(2)，n,1) + paramHat(3);estsSim(我:)= logn3fit (xSim);结束标准（ESTSIM）

Ans = 0.1542 0.0908 0.1303

观察估计的分布，检查近似正态假设对这个样本量是否合理，或检查偏差，也可能是有用的。

次要情节(3,1,1),嘘(estsSim (: 1), 20);标题(“Log-Location参数引导估计”）;次要情节(3、1、2),嘘(estsSim (:, 2), 20);标题(“对数刻度参数引导估计”）;次要情节(3、1,3),嘘(estsSim (:, 3), 20);标题(“阈值参数引导估计”）;

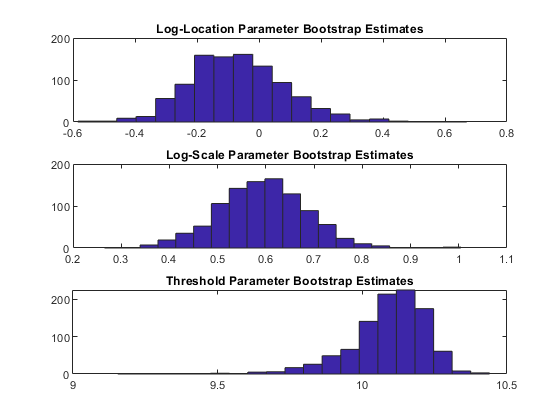
显然，阈值参数的估计量是偏斜的。这是意料之中的，因为它是由最小数据值限制的。另外两个直方图表明，对于log-location参数(第一个直方图)，近似正态性可能也是一个有问题的假设。在解释上述计算的标准误差时，必须记住这一点，并且置信区间的通常构造可能不适用于日志位置和阈值参数。

模拟估计值的平均值接近用于生成模拟数据的参数值，这表明在这个样本量下，至少对于接近估计值的参数值，该过程近似无偏。

[paramHat;意思是(estsSim)]

Ans = -0.0698 0.5930 10.1045 -0.0690 0.5926 10.0905

最后，我们还可以使用这个函数bootstrp计算引导标准误差估计。这些不会对数据进行任何参数化假设。

estsBoot=bootstrp（1000，@logn3fit，x）；标准（estsBoot）

Ans = 0.1490 0.0785 0.1180

bootstrap标准误差与蒙特卡罗计算相差不远。这并不奇怪，因为拟合模型与生成示例数据的模型相同。

总结

这里描述的拟合方法是最大似然的另一种选择，当最大似然不能提供有用的参数估计时，可以用来拟合单变量分布。一个重要的应用是拟合涉及阈值参数的分布，例如三参数对数正态分布。标准误差比最大似然估计更难计算，因为不存在解析近似，但模拟提供了一种可行的替代方法。

此处用于说明拟合方法的P-P图本身就很有用，作为拟合单变量分布时缺乏拟合的直观指示。