用广义线性模型拟合数据
这个例子展示了如何使用glmfit和格林瓦尔.普通线性回归可以用来拟合直线,或任何函数的参数是线性的,以数据正态分布的误差。这是最常用的回归模型;然而,这并不总是现实的。广义线性模型从两方面扩展了线性模型。首先,通过引入连杆函数,放宽了参数线性的假设。第二,可以对除正态分布以外的误差分布进行建模
广义线性模型
回归模型用一个或多个预测变量(通常表示为x1, x2等)定义响应变量(通常表示为y)的分布。最常用的回归模型,普通线性回归,模型y作为一个正态随机变量,其均值是预测器的线性函数,b0 + b1*x1 +…,其方差是常数。在单个预测器x的最简单情况下,模型可以表示为每一点的高斯分布直线。
Mu = @(x) -1.9+.23*x;x = 5: .1:15;yhat =μ(x);dy = -3.5: .1:3.5;深圳=大小(dy);k =(长度(dy) + 1) / 2;x1 = 7 * 1(深圳);日元=μ(x1) + dy;z1 = normpdf(μ(x1)、日元1);x2 = 10 * 1(深圳); y2 = mu(x2)+dy; z2 = normpdf(y2,mu(x2),1); x3 = 13*ones(sz); y3 = mu(x3)+dy; z3 = normpdf(y3,mu(x3),1); plot3(x,yhat,zeros(size(x)),“b -”,...x1,y1,z1,“r-”,x1([k]),y1([k]),[0 z1(k)],“:”,...x2,y2,z2,“r-”,x2([kk]),y2([kk]),[0z2(k)],“:”,...x3,y3,z3,“r-”,x3([kk]),y3([kk]),[0z3(k)],“:”); zlim([01]);xlabel(“X”);伊莱贝尔(“Y”);兹拉贝尔(的概率密度);网格在;视图(45 [-45]);

在广义线性模型中,响应的均值被建模为预测器g(b0 + b1*x1 +…)的线性函数的单调非线性变换。变换g的逆称为“连杆”函数。示例包括logit (sigmoid)链接和log链接。y也可以是非正态分布,如二项分布或泊松分布。例如,具有对数链接和单个预测器x的泊松回归可以表示为每一点具有泊松分布的指数曲线。
Mu = @(x) exp(-1.9+.23*x);x = 5: .1:15;yhat =μ(x);x1 = 7 * 1(1、5);日元= 0:4;z1 = poisspdf(μ(x1)日元);x2 = 10 * 1 (7);y2 = 0:6;z2 = poisspdf (y2,μ(x2));x3 = 13 * 1 (9); y3 = 0:8; z3 = poisspdf(y3,mu(x3)); plot3(x,yhat,zeros(size(x)),“b -”,...[x1;x1],[y1;y1],[z1;零(大小(y1)),“r-”(x1, y1, z1,“r.”,...[x2;x2],[y2;y2],[z2;零(大小(y2))],“r-”,x2,y2,z2,“r.”,...[x3;x3],[y3;y3],[z3;零(大小(y3)),“r-”,x3,y3,z3,“r.”); zlim([01]);xlabel(“X”);伊莱贝尔(“Y”);兹拉贝尔(“概率”);网格在;视图(45 [-45]);
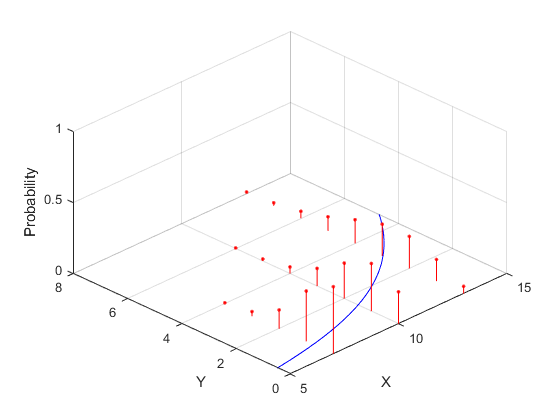
拟合Logistic回归
这个例子包括一个实验,以帮助模拟不同重量的汽车在里程测试中失败的比例。数据包括对重量、测试汽车数量和失败汽车数量的观察。
一套汽车重量重量= [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';%在每种重量下测试的汽车数量测试=[48 42 31 34 31 21 23 21 16 17 21];每一重量未通过测试的汽车数量Failed = [1 2 0 3 8 8 14 17 19 15 17 21]';%每种重量的汽车故障比例比例=失败/测试;绘图(重量、比例、,'s')包含(“重量”);伊莱贝尔(“比例”);

这张图是失败汽车的比例,作为重量的函数。可以合理地假设失效计数来自二项分布,概率参数P随着权重的增加而增加。但是P是如何依赖于重量的呢?
我们可以试着用一条直线拟合这些数据。
linearCoef = polyfit(重量比例1);linearFit = polyval (linearCoef、重量);情节(重量、比例、's',重量,直线度,“r-”,[2000 4500],[0 0],凯西:”,[2000 4500],[1 1],凯西:”)包含(“重量”);伊莱贝尔(“比例”);

此线性拟合存在两个问题:
1)该线预测小于0和大于1的比例。
2) 比例不是正态分布,因为它们必然是有界的。这违反了拟合简单线性回归模型所需的一个假设。
使用高阶多项式可能会有帮助。
[CubicRef,stats,ctr]=polyfit(权重,比例,3);cubicFit=polyval(CubicRef,权重,[],ctr);绘图(权重,比例,'s',重量,立方英尺,“r-”,[2000 4500],[0 0],凯西:”,[2000 4500],[1 1],凯西:”)包含(“重量”);伊莱贝尔(“比例”);

然而,这种配合仍然存在类似的问题。图表显示,当重量超过4000时,拟合比例开始下降;事实上,对于较大的权重值,它将变为负值。当然,正态分布的假设仍然被违背。
相反,更好的方法是使用glmfit拟合逻辑回归模型。逻辑回归是广义线性模型的一种特殊情况,对于这些数据,逻辑回归比线性回归更合适,原因有二。首先,它使用了适合二项分布的拟合方法。其次,物流环节将预测比例限制在[0,1]范围内。
对于logistic回归,我们指定了预测矩阵,以及一个矩阵,其中一列包含故障计数,一列包含测试数。我们还指定了二项分布和logit链接。
[logitCoef,dev] = glmfit(weight,[failed tested],“二”,“罗吉特”); logitFit=glmval(logitcef,重量,“罗吉特”); 绘图(重量、比例、,“bs”,重量,登录信息,“r-”);xlabel(“重量”);伊莱贝尔(“比例”);

如图所示,随着重量变小或变大,拟合比例渐近于零和一。
模型诊断
这个glmfit函数提供了一些输出,用于检查模型的适用性和测试模型。例如,我们可以比较两个模型的偏差值,以确定平方项是否会显著改善拟合。
[logitCoef2,dev2]=glmfit([weight.^2],[tested failed],“二”,“罗吉特”);pval=1-chi2cdf(dev-dev2,1)
pval = 0.4019
较大的p值表明,对于这些数据,二次项不会显著改善拟合。两次拟合的曲线图显示拟合之间几乎没有差异。
logitFit2=glmval(logitCoef2,[weight.^2],“罗吉特”); 绘图(重量、比例、,“bs”,重量,登录信息,“r-”、重量、logitFit2“g-”);传奇(“数据”,“线性项”,“线性和二次项”,“位置”,“西北”);

为了检查拟合优度,我们还可以查看Pearson残差的概率图。这些残差被标准化,以便当模型与数据合理拟合时,它们具有大致的标准正态分布。(如果没有这种标准化,残差将具有不同的方差。)
[logitCoef,dev,stats] = glmfit(weight,[failed tested],“二”,“罗吉特”)标准图(统计残差);
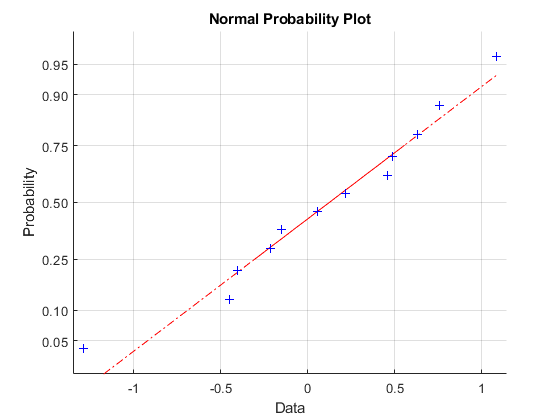
残差图与正态分布很好地吻合。
评估模型预测
一旦我们对模型感到满意,我们就可以用它来进行预测,包括计算置信区间。在这里,我们预测了100辆测试的汽车中,在四个权重中的每一个都会通过里程测试的预期数量。
weightPred=2500:500:4000;[failedPred,dlo,dhi]=glmval(LogitRef,weightPred,“罗吉特”,统计数据,.95100);错误条(权重预测、失败预测、dlo、dhi、,':');

二项模型的链接函数
对于这五个分布中的每一个glmfit金宝app支持,有一个规范的(默认的)链接函数。对于二项分布,规范的连接是logit。然而,对于二项模型来说,还有其他三个联系是合理的。所有四个都保持在区间[0,1]内的平均响应。
η= 5:.1:5;Plot (eta,1 ./ (1 + exp(-eta))'-'埃塔,normcdf (eta),'-',...预计到达时间,1-exp(-exp(eta)),'-'埃塔,exp (exp (eta)),'-');xlabel(“预测的线性函数”);伊莱贝尔(“预测平均响应”);传奇(“罗吉特”,“可能吧”,互补的双对数的,“日志”,“位置”,“东方”);

例如,我们可以将带有probit链接的fit与带有logit链接的fit进行比较。
概率系数=glmfit(重量,[测试失败],“二”,“可能吧”);probitFit = glmval (probitCoef、重量、“可能吧”); 绘图(重量、比例、,“bs”,重量,登录信息,“r-”,重量,概率,“g-”);传奇(“数据”,“Logit模型”,“Probit模型”,“位置”,“西北”);
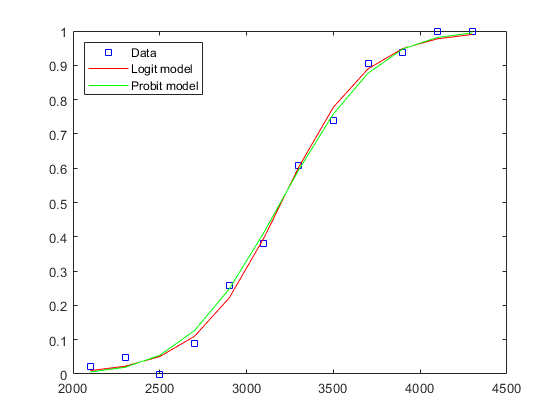
数据通常很难区分这四种链接功能,通常是在理论基础上做出选择。

