功能衍生品教程

打开生活的脚本

这个例子展示了如何使用波动方程的例子在Symbolic Math Toolbox™中使用函数导数。这个例子执行符号化计算以获得解析结果。用泛函导数求解两端固定弦的波动方程。一个函数的导数是一个函数对它所依赖的函数的导数。符号数学工具箱™使用functionalDerivative函数。

求解波动方程是泛函导数的一个应用。它描述了波的运动，从弦的运动到电磁波的传播，是物理学中一个重要的方程。你可以将这个例子中所说明的技术应用到变化法的应用中，从解决腕时问题到寻找最小的肥皂泡表面。

考虑一个长度的字符串l悬浮在两点之间x = 0和x = L。弦的单位长度有一个特征密度和一个特征张力。将长度、密度和张力定义为常数以备以后使用。为简单起见，将这些常量设置为1。

长度= 1;密度= 1;张力= 1;

如果弦在运动，弦的动能和势能是它相对静止的位移的函数S (x, t)，它随位置而变化x和时间t。如果d每单位长度的密度，动能是多少

$T = \int_{0}^{l} \frac{d}{2} {(\frac{d}{d t} 年代 (x, t))}^{2} d x 。$

势能是

$V = \int_{0}^{l} \frac{r}{2} {(\frac{d}{d x} 年代 (x, t))}^{2} d x,$

在哪里r是紧张的。

在MATLAB®中输入这些方程。因为length必须是正的，所以设这个假设。这种假设允许简化将所得方程简化成期望形式。

信谊S (x, t)drvl假设(L>0) T(x, T) = int(d/2*diff(S, T)^2,x,0,L);V (x, t) = int (r / 2 * diff(年代,x) ^ 2, x, 0, L);

这个动作一个是过程。最小作用量原理说明作用量总是最小的。求的函数导数，确定最小作用量的条件一个关于年代使用functionalDerivative让它等于零。

一个=过程;eqn =函数导数(A,S) == 0

eqn (x, t) =
                
                  $l r \frac{\partial^{2}}{\partial x^{2}} 年代 (x, t) - l d \frac{\partial^{2}}{\partial t^{2}} 年代 (x, t) = 0$

用简化方程简化。代入，将方程转化为其期望形式r / d用波速的平方v。

eqn =简化(eqn) / r;eqn =潜艇(eqn, r / d, v ^ 2)

eqn (x, t) =
                
                  $\frac{\frac{\partial^{2}}{\partial t^{2}} 年代 (x, t)}{v^{2}} = \frac{\partial^{2}}{\partial x^{2}} 年代 (x, t)$

用分离变量法求解方程。集S (x, t) = U (x) * V (t)分开对位置的依赖x和时间t。将得到的方程两边分开孩子们。

信谊U (x)V (t)eqn2 =潜艇(eqn S (x, t), U (x) * V (t));eqn2 = eqn2 / (U (x) * V (t))

eqn2 (x, t) =
                
                  $\frac{\frac{\partial^{2}}{\partial t^{2}} V (t)}{v^{2} V (t)} = \frac{\frac{\partial^{2}}{\partial x^{2}} U (x)}{U (x)}$

tmp =孩子(eqn2);

方程的两边取决于不同的变量，但它们是相等的。这只有在两边都是常数的情况下才可能。使每条边等于一个任意常数C得到两个微分方程。

信谊C2 . C = 1

eqn3 =
                
                  $\frac{\frac{\partial^{2}}{\partial t^{2}} V (t)}{v^{2} V (t)} = C$

eqn4 = tmp(2) == C

eqn4 =
                
                  $\frac{\frac{\partial^{2}}{\partial x^{2}} U (x)}{U (x)} = C$

解微分方程dsolve在位移为0在x = 0和t = 0。用下列方法将方程式简化为预期形式简化与步骤选项设置为50。

V (t) = dsolve (eqn3, V (0) = = 0, t);U (x) = dsolve (eqn4 U (0) = = 0, x);V (t) =简化(V (t)“步骤”, 50)

V (t) =
                 $- 2 C_{1} \sinh (\sqrt{C} t v)$

U (x) =简化(U (x),“步骤”, 50)

U (x) =
                 $2 C_{1} \sinh (\sqrt{C} x)$

求出方程中的常数。

p1 = setdiff (symvar (U (x))信谊((C、x)))

p1 =
                 $C_{1}$

p2 = setdiff (symvar (V (t)),信谊((C、V、t)))

p2 =
                 $C_{1}$

弦在位置上是固定的x = 0和x = L。的条件U (0) = 0已经存在。应用边界条件U (L) = 0和解决C。

eqn_bc = U(L) == 0;[solC,参数,气孔导度]=解决(eqn_bc C“ReturnConditions”,真正的)

solC =
                
                  $- \frac{k^{2} π^{2}}{l^{2}}$

param =
                 $k$

气孔导度=
                 $C_{1} \neq 0 \land 1 \leq k \land k \in Z$

假设(电导率)

解决方案S (x, t)是U (x)和V (t)。求出解，将字符串的特征值代入解中，得到解的最终形式。

S (x, t) = U (x) * V (t);S =潜艇(S、C、solC);S = sub (S，[L v]，[长度sqrt(张力/密度)]);

的参数p1和p2确定振动的振幅。集p1和p2来1为了简单起见。

S = subs(S，[p1 p2]，[1 1]);S =简化(年代,“步骤”, 50)

S (x, t) =
                 $4 罪 (π k t) 罪 (π k x)$

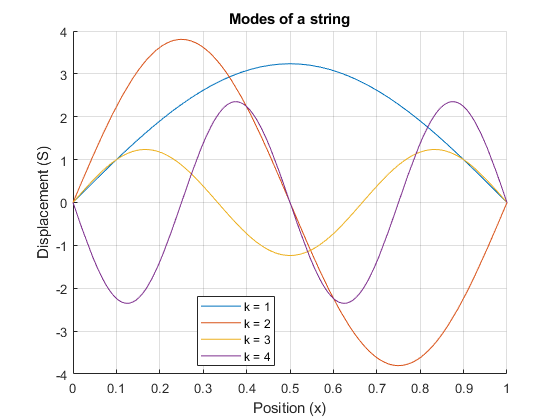
对于不同的值，弦有不同的振动模式k。为任意的时间值绘制前四种模式t。使用参数返回的参数解决为了解决参数k。

Splot (x) = S (x, 0.3);图(1)在网格在ymin =双(多项式系数(Splot));为yplot = subs(Splot,param,i);fplot (yplot长度[0])结束ylim ([-ymin ymin])传说(“k = 1”,“k = 2”,“k = 3”,“k = 4”,“位置”,“最佳”)包含(“位置(x)”) ylabel (“位移(S)”)标题(字符串的模式)

波动方程是线性的。这意味着，所允许的模态的任何线性组合都是波动方程的有效解。因此，在给定边界条件和初值下，波动方程的完全解是所允许模态的和

$F (x, t) = \sum_{k = n}^{米} {一个}_{k} 罪 (π k t) 罪 (π k x),$

在哪里 ${一个}_{k}$ 表示任意常数。

使用symsum将弦的前五种模式相加。在新图形上，将产生的波形与先前的波形在同一时间显示，以便比较。

图(2)S5(x) = 1/5*symsum(S,param,1,5);fplot(subs(S5,t,0.3)，[0长度])ylim([-ymin ymin])网格在包含(“位置(x)”) ylabel (“位移(S)”)标题(“前5种模式的总和”)

图中显示，求和模式允许你建模一个定性不同的波形。这里，我们指定初始条件为 $年代 (x, t = 0) = 0$ 对所有 $x$ 。

你可以计算这些值 ${一个}_{k}$ 在方程中 $F (x, t) = \sum_{k = n}^{米} {一个}_{k} 罪 (π k t) 罪 (π k x)$ 通过指定初始速度的条件

$u_{t} (x, t = 0) = F_{t} (x, 0) 。$

适当的模态求和可以表示任何波形，这与使用傅立叶级数表示弦的运动是一样的。

符号数学工具箱文档

金宝app

用符号数学工具箱进行数学建模

获取示例和视频