求解非线性传热偏微分方程

这个示例使用:

该示例说明了如何在薄板中求解非线性传热的局部微分方程（PDE）。

板为方形，其温度沿底边固定。由于其他三条边是绝缘的，所以没有热量从其他三条边转移。热量通过对流和辐射从板的上下两面传递。因为包括了辐射，所以这个问题是非线性的。

本示例的目的是演示如何使用Symbolic Math Toolbox™符号表示非线性偏微分方程，并使用symbol Math Toolbox™解决偏微分方程问题有限元分析在偏微分方程工具箱™。在本例中，进行瞬态分析，求解板内温度随时间的函数。瞬态分析显示了板在稳定状态下达到平衡温度所需要的时间。

平板传热方程

平板的平面尺寸为1米乘1米，厚度为1厘米。由于平板相对于平面尺寸来说相对较薄，因此可以假设温度在厚度方向上是恒定的，由此产生的问题是二维的。

假设对流和辐射热传输在板的两个面和具有特定环境温度的环境之间进行。

由于对流从每个板面在单位面积内传递的热量定义为

$问_{c} ＝ h_{c} （ T - T_{一个} ）$ ，

在哪里 $T_{一个}$ 为环境温度， $T$ 温度是特定的吗 $x$ 和 $y$ 定位在板表面，和 $h_{c}$ 为指定的对流系数。

在单位面积内，由于辐射从每个板面传递的热量定义为

$问_{r} ＝ ε. σ （ T^{4} - T_{一个}^{4} ）$ ，

在哪里 $ε.$ 是脸的辐射率和 $σ$ 是斯特凡-玻尔兹曼常数。由于辐射传递的热量与表面温度的四次方成正比，所以这个问题是非线性的。

描述薄板温度的偏微分方程为

$ρ C_{p} t_{z} \frac{\partial T}{\partial t} - k t_{z} \nabla^{2} T + 2 问_{c} + 2 问_{r} ＝ 0$

在哪里 $ρ$ 为板材的材料密度， $C_{p}$ 是它的比热， $t_{z}$ 为板厚， $k$ 是它的热导率，这两个因素解释了从它的两个面传热。

PDE参数定义

通过定义参数的值来设置PDE问题。该板由铜构成，具有以下性质。

kmentrmal = 400;铜热导率%，W/(m-K)rhoCopper = 8960;%铜密度，kg/m^3specificHeat = 386;铜比热% J/(kg-K)厚= 0.01;%板厚，单位为米stefanBoltz = 5.670373 e-8;% Stefan-Boltzmann常数，W/(m^2-K^4)hCoeff = 1;%对流系数W/(m^2-K)tAmbient = 300;环境温度%工作= 0.5;板面发射率%

提取PDE系数

以板温为因变量，用符号形式定义偏微分方程 $T （ t ， x ， y ）$ ．

信谊T (T, x, y)信谊每股收益团体tzhc助教ρCpkQc = hc*(T - Ta);Qr = eps*sig*(T^4 - Ta^4);pdeeq =(ρ* Cp * tz *差异(T, T) - k * tz *拉普拉斯算子(T (x, y)) + 2 * Qc + 2 * Qr)

Pdeeq (t, x, y) =
                 
                   $2 每股收益 团体 ({T （ t ， x ， y ）}^{4} - {助教}^{4}) - k tz (\frac{\partial^{2}}{\partial x^{2}} T （ t ， x ， y ） + \frac{\partial^{2}}{\partial y^{2}} T （ t ， x ， y ）) - 2 hc (助教 - T （ t ， x ， y ）) + Cp ρ tz \frac{\partial}{\partial t} T （ t ， x ， y ）$

现在，根据偏微分方程工具箱的要求，创建用于在PDE模型中作为输入的系数。要做到这一点，首先提取符号PDE的系数作为符号表达式的结构pdeCoefficients函数。

symCoeffs = pdeCoefficients (pdeeq T“象征”,真正的)

symCoeffs =结构体字段:M：[1x1 sym] a：[1x1 sym] c：[2x2 sym] f：[1x1 sym] d：[1x1 sym]

接下来，用数字值替换表示PDE参数的符号变量。

symVars = [eps sig tz hc Ta rho Cp k];symVals = [miss stefanBoltz thick hCoeff tAmbient rhoCopper specificHeat kThermal];symCoeffs =潜艇(symCoeffs symVars symVals);

最后，自田地symCoeffs符号对象，使用pdeCoefficientsToDouble函数将系数转换为双数据类型，这使它们成为偏微分方程工具箱的有效输入。

coeffs = pdecoeffitialstodouble（Symcoeffs）

多项式系数=结构体字段:答：@ MakeCoeFirition / CoeffITyFunction C：[4x1 Double] M：0 D：3.4586E + 04 F：1.0593E + 03

指定PDE模型、几何和系数

现在，利用偏微分方程工具箱，利用基于这些系数的有限元分析来求解偏微分方程问题。

首先，创建带有单个因变量的PDE模型。

numberOfPDE = 1;模型= createpde (numberOfPDE);

指定PDE模型的几何形状——在本例中是正方形的尺寸。

宽度= 1;身高= 1;

定义几何描述矩阵。使用该方案创建正方形几何decsg(偏微分方程工具箱)函数。对于矩形几何，第一行包含3.，第二行包含4．接下来的四行包含 $x$ - 边缘的起点和四行包含的内容 $y$ -边缘起始点的坐标。

GDM = [3 4 0 width width 0 0 0 height height]';g = decsg (gdm,“S1 '，（“S1 ') ');

将DECSG几何图形转换为一个几何对象，并将其包含在PDE模型中。

geometryFromEdges(模型中,g);

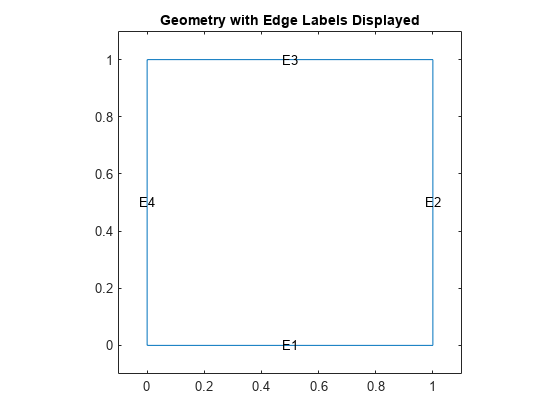
绘制几何形状并显示边缘标签。

图;pdegplot(模型,'Edgelabels'，“上”）;轴([-0.1 1.1 -0.1 1.1]);标题(“显示边缘标签的几何图形”）;

图中包含一个坐标轴。标题为“显示几何边缘标签”的轴包含5个类型为行、文本的对象。

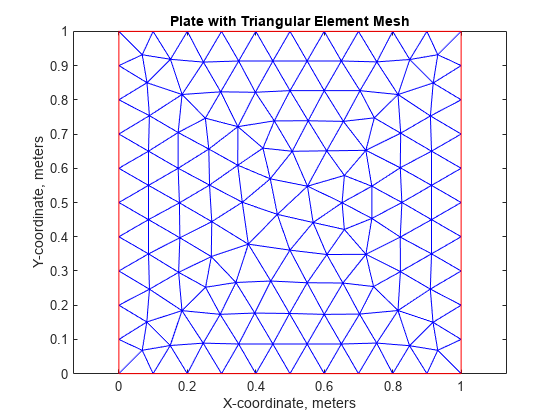
接下来，在PDE模型中创建每个方向的网格大小约为0.1的三角形网格。

hmax = 0.1;%的元素大小msh = generateMesh(模型,“Hmax”, hmax);图;pdeplot(模型);轴平等的标题(“带有三角形网格元素的板”）;包含(“x坐标,米”）;ylabel (“坐标,米”）;

图中包含一个坐标轴。以三角网格为标题的板轴包含2个线条对象。

指定PDE模型中的系数。

specifyCoefficients(模型,“米”，coeffs.m，' d 'coeffs.d,．..“c”coeffs.c,“一个”coeffs.a,“f”, coeffs.f);

找到临时解决方案

应用边界条件。板的三条边是绝缘的。因为在有限元公式中，诺伊曼边界条件等于零是默认值，所以你不需要在这些边上设置边界条件。板的底边固定在1000 K。在底边(边E1)的所有节点上使用Dirichlet条件指定此参数。

applyBoundaryCondition(模型,“边界条件”，“边缘”, 1“u”, 1000);

指定初始温度为0 K，除了底部边缘。将下边缘E1的初始温度设置为恒定边界条件的值，1000k。

setInitialConditions(模型中,0);1000年setInitialConditions(模型,“边缘”1);

定义时域，求偏微分方程的暂态解。

endTime = 10000;tlist = 0:50: endTime;

设置求解器选项的公差。

model.SolverOptions.RelativeTolerance = 1.0 e - 3;model.SolverOptions.AbsoluteTolerance = 1.0的军医;

使用方法解决问题solvepde．将温度沿板顶沿绘制成时间的函数。

R = solvepde(模型、tlist);u = R.NodalSolution;图;:情节(tlist u (3));网格上标题“沿板块顶部边缘的温度与时间的关系”包含“时间(s)”ylabel“温度(K)”

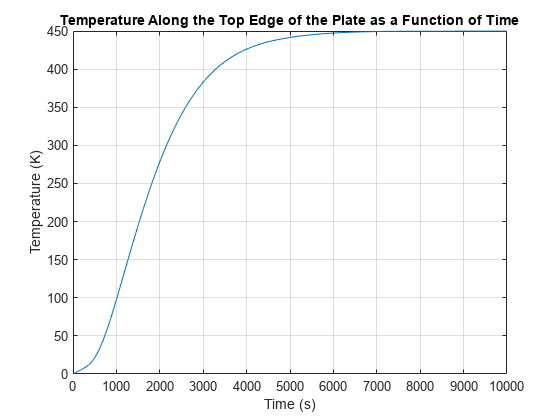
图中包含一个坐标轴。标题为“沿板顶沿温度随时间变化”的轴包含一个线型对象。

由图可知，瞬态解在6000秒后开始达到稳态值。6000秒后，顶部边缘的平衡温度接近450 K。

显示10,000秒后板的温度曲线。

图;pdeplot(模型,“XYData”u(:,结束),“轮廓”，“上”，“ColorMap”，“喷气机”）;标题(sprintf ('极板内温度，瞬态溶液(%d秒)\n'，．..tlist (1)));包含“x坐标,米”ylabel“坐标,米”轴平等的；

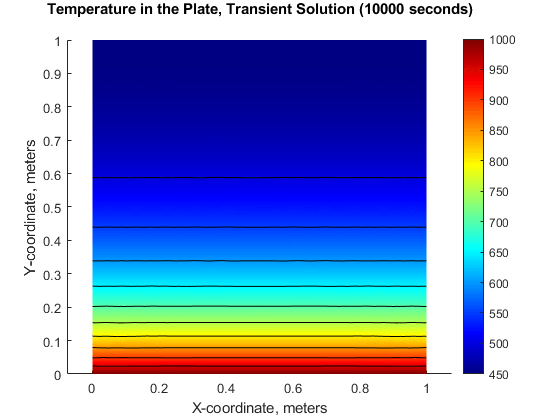
图中包含一个坐标轴。标题为“板内温度，瞬态溶液(10000秒)”的轴包含12个类型为patch, line的对象。

显示顶部边缘10,000秒的温度。

u (3)

ans = 449.8031

求解非线性传热偏微分方程

平板传热方程

PDE参数定义

提取PDE系数

指定PDE模型、几何和系数

找到临时解决方案

符号数学工具箱文档

金宝app

数学建模与符号数学工具箱