利用符号数学优化工具箱™ 解算器

此示例使用：

打开实时脚本

此示例演示如何使用符号数学工具箱™ 功能雅各比亚和matlabFunction为优化解算器提供分析导数。优化工具箱™ 当您提供目标函数和约束函数的梯度和Hessian值时，解算器通常更精确、更高效。

基于问题的优化可以自动计算和使用渐变；请参阅优化工具箱中自动差异化（优化工具箱）。有关使用自动微分的基于问题的示例，请参阅基于问题的约束静电非线性优化（优化工具箱）。

使用具有优化功能的符号计算有几个考虑因素：

优化目标和约束函数应该用向量来定义，比如X。但是，符号变量是标量或复数，而不是向量值。这要求您在向量和标量之间进行转换。
优化梯度，有时是Hessian，应该在目标函数或约束函数体内计算。这意味着符号梯度或Hessian必须放置在目标函数或约束函数文件或函数句柄中的适当位置。
计算梯度和象征性象征性可能是耗时的。因此，您应该只执行此计算一次，并通过matlabFunction，以在执行解算器期间调用。
评估象征性表达subs功能是耗时的。使用更有效matlabFunction。
matlabFunction生成取决于输入向量方向的代码。自从粉刺使用列向量调用目标函数时，必须小心调用matlabFunction使用符号变量的列向量。

第一个例子：与黑森州的无约束最小化

最小化的目标函数是：

$F （ X_{1} 那 X_{2} ） = 日志（ 1 + 3. {（ X_{2} - （ X_{1}^{3.} - X_{1} ））}^{2} + （ X_{1} - 4. / 3. ）^{2} ）。$

此函数为正值，在以下情况下获得唯一的最小值零：X1= 4/3,X2=(4/3)^3 - 4/3 = 1.0370...

我们把自变量写成X1和X2因为在这种形式下，它们可以用作符号变量。作为向量的组成部分X他们会被写下来x（1）和x（2）.如下图所示，该功能有一个曲折的山谷。

Syms.X1X2真实的x = [x1; x2];％列矢量的符号变量f=对数（1+3*（x2-（x1^3-x1））^2+（x1-4/3）^2）

f=
                 
                   $日志 （ {(X_{1} - \frac{4.}{3.})}^{2} + 3. {(- {X_{1}}^{3.} + X_{1} + X_{2})}^{2} + 1 ）$

fsurf（f，[-2]，“展示轮廓”那'在'）查看（127,38）

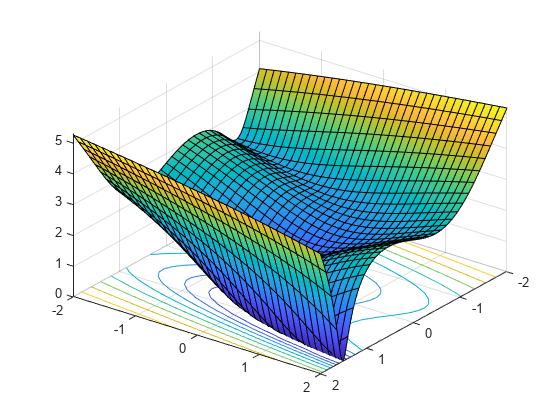
计算f的梯度和Hessian：

gradf=雅可比（f，x）。'％列gracf.

格拉夫=
                 
                   $\begin{array}{l} （ \begin{array}{c} - \frac{6. (3. {X_{1}}^{2} - 1) (- {X_{1}}^{3.} + X_{1} + X_{2}) - 2 X_{1} + \frac{8.}{3.}}{σ_{1}} \\ \frac{- 6. {X_{1}}^{3.} + 6. X_{1} + 6. X_{2}}{σ_{1}} \end{array} ） \\ 在哪里 \\ σ_{1} = {(X_{1} - \frac{4.}{3.})}^{2} + 3. {(- {X_{1}}^{3.} + X_{1} + X_{2})}^{2} + 1 \end{array}$

hessf=雅可比（gradf，x）

赫斯夫=
                 
                   $\begin{array}{l} （ \begin{array}{c} \frac{6. {(3. {X_{1}}^{2} - 1)}^{2} - 36. X_{1} (- {X_{1}}^{3.} + X_{1} + X_{2}) + 2}{σ_{2}} - \frac{{σ_{3.}}^{2}}{{σ_{2}}^{2}} & σ_{1} \\ σ_{1} & \frac{6.}{σ_{2}} - \frac{{(- 6. {X_{1}}^{3.} + 6. X_{1} + 6. X_{2})}^{2}}{{σ_{2}}^{2}} \end{array} ） \\ 在哪里 \\ σ_{1} = \frac{(- 6. {X_{1}}^{3.} + 6. X_{1} + 6. X_{2}) σ_{3.}}{{σ_{2}}^{2}} - \frac{18. {X_{1}}^{2} - 6.}{σ_{2}} \\ σ_{2} = {(X_{1} - \frac{4.}{3.})}^{2} + 3. {(- {X_{1}}^{3.} + X_{1} + X_{2})}^{2} + 1 \\ σ_{3.} = 6. (3. {X_{1}}^{2} - 1) (- {X_{1}}^{3.} + X_{1} + X_{2}) - 2 X_{1} + \frac{8.}{3.} \end{array}$

这Fminunc.求解器预计将通过向量x，而且specifyobjectivegradient.选项设置为符合事实的和赫索斯·福克选项设置为“目标”，预计三个输出列表：[f（x），gradf（x），hessf（x）]。

matlabFunction从三个输入列表中确切地生成三个输出列表。此外，使用vars.选项matlabFunction接受向量输入。

fh=matlabFunction（f，gradf，hessf，'vars'，{x}）；

现在从点[-1,2]开始求解最小化问题：

选项=最佳选项('fminunc'那......“SpecificyObjectiveGradient”符合事实的......“HessianFcn”那“目标”那......“算法”那“信任区”那......“显示”那“决赛”)；[xfinal，fval，exitflag，output]=fminunc（fh，[-1；2]，选项）

可能的局部最小值。fminunc停止，因为功能值相对于其初始值的最终变化小于功能公差值。

Xfinal =2×11.3333 1.0370

fval=7.6623e-12

exitflag=3

输出=带字段的结构：迭代次数：14 funcCount:15步长：0.0027 cGaterations:11 firstorderopt:3.4391e-05算法：“信任区域”消息：“…”冲突：[]

将其与不使用梯度或Hessian信息的迭代次数进行比较“拟牛顿”算法。

选项=最佳选项('fminunc'那“显示”那“决赛”那“算法”那“拟牛顿”)；fh2=matlabFunction（f，'vars'，{x}）；％fh2 =目的没有梯度或黑森州[xfinal，fval，exitflag，output2]=fminunc（fh2，[-1；2]，选项）

发现本地最低限度。优化完成，因为梯度的大小小于最优耐受性的值。

Xfinal =2×11.3333 1.0371

fval=2.1985e-11

exitflag=1

Output2 =带字段的结构：迭代次数：18次funcCount:81步长：2.1164e-04 lssteplength:1 firstorderopt:2.4587e-06算法：“拟牛顿”消息：“…”

使用渐变和Hessians时，迭代次数较低，并且函数评估较少：

Sprintf（[“使用渐变”有％d迭代'......'和赫森，但没有他们％d。'],......output.iterations，output2.iterations）

ans ='使用渐变和黑森州有14个迭代，但是没有它们18。“

Sprintf（['使用梯度进行了%d次函数计算'......'和赫森，但没有他们％d。'],......output.funcCount，output2.funcCount）

ans=“有15个函数评估使用梯度和Hessian，但81个没有。”

第二示例：使用Fmincon内部点算法约束最小化

我们考虑相同的目标函数和起点，但现在有两个非线性约束：

$5. Sinh. （ X_{2} / 5. ） \geq X_{1}^{4.}$

$5. 塔尼（ X_{1} / 5. ） \geq X_{2}^{2} - 1 。$

约束使优化远离全局最小点[1.333,1.037]。可视化两个约束：

[X，Y]=meshgrid（-2:01:3）；Z=（5*sinh（Y./5）>=X.^4）；%Z=1，其中满足第一个约束，否则Z=0z = z + 2 *（5 * tanh（x./5）> = y. ^ 2  -  1）;％z = 2，其中秒的满足，z = 3两个冲浪（x，y，z，“线条样式”那“没有”）;图= GCF;图.Color =.“w”;%白色背景视图（0,90）保持在…上图3（.4396、.0373、4、，“哦”那“MarkerEdgeColor”那'r'那“MarkerSize”,8);%最佳点xlabel(“x”)伊拉贝尔(“是的”)持有关

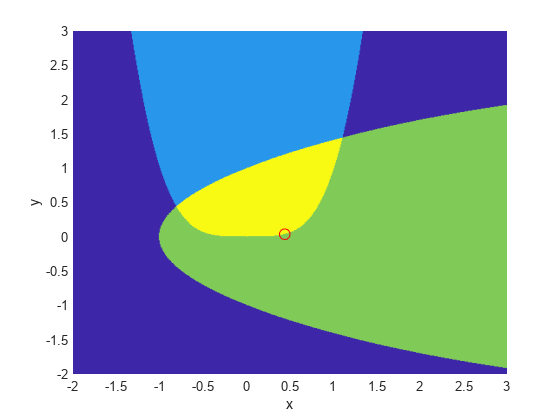
我们在最佳点周围画了一个红色的小圆圈。

下面是可行区域上的目标函数图，该区域满足两个约束条件，上图为深红色，以及围绕最佳点的红色小圆：

w = log（1 + 3 *（y  - （x. ^ 3  -  x））。^ 2 +（x  -  4/3）。^ 2）;％w =目标函数w（z <3）= nan;只有约束满足的％绘图冲浪（x，y，w，“线条样式”那“没有”)；视图（68,20）保持不变在…上图3（.4396、.0373、.8152、，“哦”那“MarkerEdgeColor”那'r'那......“MarkerSize”,8);%最佳点xlabel(“x”)伊拉贝尔(“是的”)兹拉贝尔(“z”)持有关

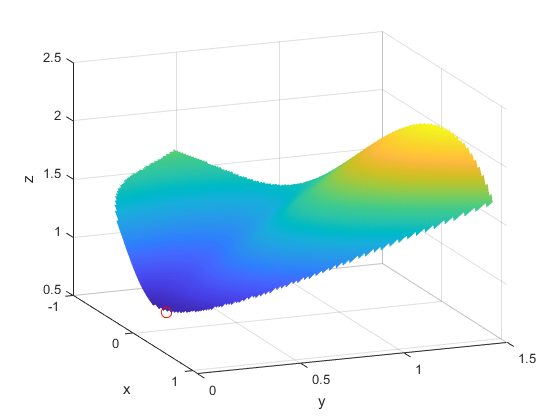
非线性约束必须写在表格中c（x）<=0.我们计算所有符号约束及其导数，并使用matlabFunction。

约束的梯度应该是列向量;它们必须将其作为矩阵放置在目标函数中，每列的矩阵表示一个约束函数的梯度。这是由此产生的表单的转置雅各比亚，所以我们采用下面的转置。

我们将非线性约束放入函数句柄中。粉刺期望非线性约束和梯度按顺序输出[C CEQ GRACC毕业典].由于没有非线性等式约束，我们输出[]为了CEQ.和梯度。

c1=x1^4-5*sinh（x2/5）；c2=x2^2-5*tanh（x1/5）-1；c=[c1 c2]；gradc=jacobian（c，x）。”；%换位以正确的形式放置约束=matlabFunction（c，[]，gradc，[]，'vars'，{x}）；

内点算法要求其Hessian函数作为单独的函数编写，而不是作为目标函数的一部分。这是因为非线性约束函数需要在其Hessian中包含这些约束。其Hessian是拉格朗日函数的Hessian；有关更多信息，请参阅用户指南。

Hessian函数接受两个输入参数：位置向量X和拉格朗日乘法器结构lambda。用于非线性约束的Lambda结构的部分是lambda.ineqnonlin.和lambda.eqnonlin..对于当前约束，没有线性等式，因此我们使用两个乘数lambda.ineqnonlin（1）和lambda.ineqnonlin（2）。

我们在第一个例子中计算了Hessian的目标函数。现在我们计算了两个约束函数的Hessians，并制作功能处理版本matlabFunction。

hessc1=雅可比（gradc（：，1），x）；%约束=第一个c列hessc2=雅可比（gradc（：，2），x）；hessfh=matlabFunction（hessf，'vars'，{x}；hessc1h=matlabFunction（hessc1，'vars'，{x}；hessc2h=matlabFunction（hessc2，'vars'，{x}）；

要制作最后的黑森州，我们将三个黑森州拿在一起，将适当的拉格朗日乘数添加到约束函数。

myhess=@（x，lambda）（hessfh（x）+......lambda.ineqnonlin（1）*hessc1h（x）+......lambda.ineqnonlin（2）*hessc2h（x））；

设置选项以使用内点算法、渐变和Hessian，使目标函数同时返回目标和渐变，并运行解算器：

选项=最佳选项(“fmincon”那......“算法”那“内点”那......“SpecificyObjectiveGradient”，真的，......“SpecifyConstraintGradient”，真的，......“HessianFcn”，myhess，......“显示”那“决赛”）;%fh2=不带Hessian的目标fh2=matlabFunction（f，gradf，'vars'，{x}）；[xfinal，fval，exitflag，output]=fmincon（fh2，[-1；2]，......[]、[]、[]、[]、[]、[]、约束、选项）

找到满足约束的局部最小值。优化完成是因为目标函数在可行方向上不递减，在最优性公差值范围内，且约束满足在约束公差值范围内。

Xfinal =2×10.4396 0.0373

fval=0.8152

exitflag=1

输出=带字段的结构：迭代：10 Funccount：13 CorroudViration：0步骤：1.9160E-06算法：'内部点'Firstordopt：1.9217E-08 Cgiterations：0消息：'...'最佳：[1x1 struct]

再次，求解器将较少的迭代和函数评估与渐变和粗糙的迭代和函数评估提供，而不是：

选项=最佳选项(“fmincon”那“算法”那“内点”那......“显示”那“决赛”）;％fh3 =没有梯度或黑森州的目标fh3 = matlabfunction（f，'vars'，{x}）；没有渐变的％约束：约束= matlabfunction（c，[]，'vars'，{x}）；[xfinal，fval，exitflag，output2]=fmincon（fh3，[-1；2]，......[]、[]、[]、[]、[]、[]、约束、选项）

找到了较低目标函数值的可行点。找到满足约束的局部最小值。优化完成是因为目标函数在可行方向上不递减，在最优性公差值范围内，且约束满足在约束公差值范围内。

Xfinal =2×10.4396 0.0373

fval=0.8152

exitflag=1

Output2 =带字段的结构：迭代次数：18次funcCount:57次迭代次数：0步长：9.6632e-07算法：“内部点”firstorderopt:3.8435e-07 cgiterations:0消息：“…”最佳可行：[1x1结构]

Sprintf（[“使用渐变”有％d迭代'......'和赫森，但没有他们％d。'],......output.iterations，output2.iterations）

ans=“使用gradient和Hessian进行了10次迭代，但没有它们的迭代有18次。”

Sprintf（['使用梯度进行了%d次函数计算'......'和赫森，但没有他们％d。'],......output.funcCount，output2.funcCount）

ans ='使用渐变和黑森州有13个功能评估，但没有它们。“

清理符号变量

本例中使用的符号变量假定为实变量。要从符号引擎工作区中清除此假设，仅删除变量是不够的。必须使用语法清除变量的假设

假设（[x1，x2]，'清除'）

当以下命令的输出为空时，所有假设都被清除

假设（[x1，x2]）

ans =空的sym：1-by-0

利用符号数学优化工具箱™ 解算器

第一个例子：与黑森州的无约束最小化

第二示例：使用Fmincon内部点算法约束最小化

清理符号变量

符号数学工具箱文档

金宝app

数学建模与符号数学工具箱