パラメトリック法

最新のリリースでは，このページがまだ翻訳されていません。このページの最新版は英语でご覧になれます。

信号长が短い场合，パラメトリック法は，ノンパラメトリック法よりも高い解像度を提供します。これら2つの方法は，スペクトル推定へのアプローチが异なるもので，データから直接PSDを推定する代わりに，データをホワイトノイズがある线形システムに入力した结果の出力として“モデル化” するもので，结果として，その线形モデルのパラメーターを推定するものです。

一般的に使用される线形システムモデルは，“全極モデル“で,ž平面の原点に，すべての零点をもつフィルターです。このようなフィルターへのホワイトノイズの出力は，自己回帰（AR）过程です。このために，これらの方法は，スペクトル推定の“AR法”と見なされます。

AR法には，ピークのあるデータ，すなわち，PSDがある周波数で大きくなるデータのスペクトルを适切に记述する倾向があります。多くの実际的アプリケーション中のデータ（たとえば音声のような）は，「ピークのあるスペクトル”を示す倾向があるため，ARモデルは多くの场合有效となります。加えて，ARモデルは，比较的简単に解くことのできる线形方程式系を导きます。

信号处理工具箱™では，スペクトル推定に対して，以下のAR法を提供しています。

すべてのAR法は，次式で得られるPSDを与えます。

$\hat{P} （ F ） = \frac{1}{F_{小号}} \frac{ε_{p}}{{| 1 - Σ_{ķ = 1}^{p} {\hat{一种}}_{p} （ ķ ） Ë^{- Ĵ 2 π ķ F / F_{小号}} |}^{2}} 。$

异なったAR法ではパラメーターをわずかに异なった形で推定し，异なったPSD推定を与えます。次の表は，种々のAR法をまとめたものです。

AR法

	バーグ	共分散	修正共分散	ユール·ウォーカー
特性	データへのウィンドウ适用なし	データへのウィンドウ适用なし	データへのウィンドウ适用なし	データにウィンドウを適用
特性	レビンソン再帰法を満たす制约のAR系数をもち，前方予测と后方予测误差を最小二乘的に最小化	前方予测误差を最小二乘的に最小化	前方および后方予测误差を最小二乘的に最小化	前方予测误差を最小二乘的に最小化（别名「自己相关法」）
利点	短いデータレコードにおける高い解像度	短いデータレコードにおける,ユール・ウォーカー法を上回る解像度(より正確な推定)	短いデータレコードにおける高い解像度	大规模データレコードにおける，他の方法に比肩する性能
	常に安定モデルを作成	pまたはより基本的な正弦波から构成されるデータからの周波数抽出が可能	pまたはより基本的な正弦波から构成されるデータからの周波数抽出が可能	常に安定モデルを作成
	常に安定モデルを作成	pまたはより基本的な正弦波から构成されるデータからの周波数抽出が可能	スペクトル线分割による损失なし	常に安定モデルを作成
欠点	ピーク位置の初期位相への高依存	不安定モデル作成の可能性	不安定モデル作成の可能性	短いデータレコードにおける相対的低性能化
	ノイズを伴うまたは高次数时の正弦波におけるスペクトル线分割による损失可能性	ノイズを伴う正弦波の推定における周波数バイアス	ピーク位置の初期位相への軽度の依存	ノイズを伴う正弦波の推定における周波数バイアス
	ノイズを伴う正弦波の推定における周波数バイアス	ノイズを伴う正弦波の推定における周波数バイアス	ノイズを伴う正弦波の推定における軽度の周波数バイアス
非特异化条件		次数が入力フレームサイズの半分以下であること	次数が入力フレームサイズの2/3以下であること	推定のバイアスにより自己相关行列の正定が保证されるため，非特异

ユール·ウォーカーAR法

ライブスクリプトを开く

スペクトル推定の “ユール·ウォーカー法”では，ユール·ウォーカー方程式を行列形式で表した次の线形システムを解くことにより，ARパラメーターが计算されます。

$[\begin{matrix} [R （ 0 ） & [R （ 1 ） & \dots & [R （ p - 1 ） \\ [R （ 1 ） & [R （ 0 ） & \dots & [R （ p - 2 ） \\ ⋮ & ⋮ & ⋱ & ⋮ \\ [R （ p - 1 ） & [R （ p - 2 ） & \dots & [R （ 0 ） \end{matrix}] [\begin{matrix} 一种（ 1 ） \\ 一种（ 2 ） \\ ⋮ \\ 一种（ p ） \end{matrix}] = [\begin{matrix} [R （ 1 ） \\ [R （ 2 ） \\ ⋮ \\ [R （ p ） \end{matrix}]$

実际には，自己相关のバイアス推定が，未知の真の自己相关に使用されます。ユール·ウォーカーAR法では，最大エントロピー推定器として同じ结果が生成されます。

自己相关关数のバイアス付き推定の使用は，上の自己相关行列が正定である必要があります。そのため，行列が可逆で，解が存在することは保证されます。さらに，计算されるARパラメーターは，安定な全极モデルに常になります。ユール·ウォーカー方程式は，自己相关行列のエルミート·テプリッツ构造を利用するレビンソンのアルゴリズムを使用して效率的に解くことができます。

このツールボックスの关数pyulearは，ユール·ウォーカーAR法を実装します。例として，ウェルチ法とユール·ウォーカーAR法を使用して，音声信号のスペクトルを求め，比较します。最初に，ウェルチピリオドグラムを计算してプロットします。

加载MTLBpwelch（MTLB，汉明（256），128,1024，FS）

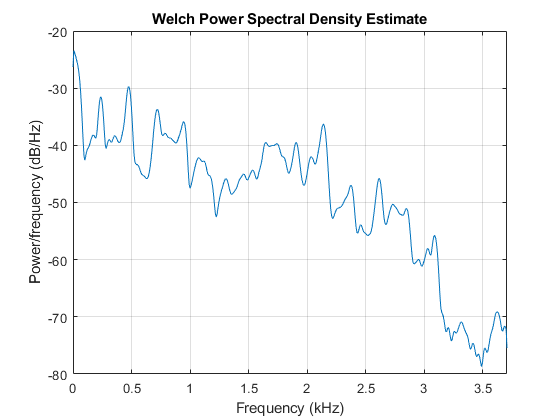
ユール·ウォーカーARスペクトルは，ピリオドグラムのものよりも，単纯な全极モデルであるために，よりスムーズです。

为了= 14;pyulear（MTLB，顺序，1024，FS）

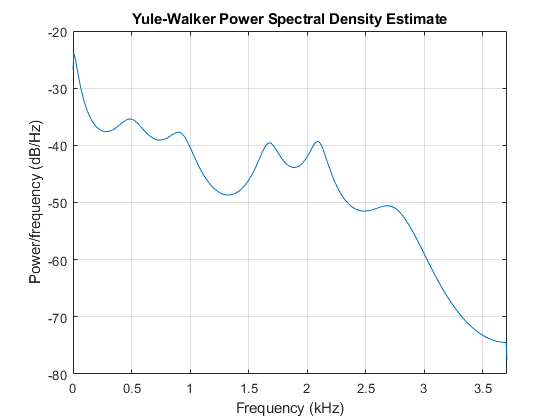
バーグ法

ライブスクリプトを开く

ARスペクトル推定のバーグ法は，レビンソン·ダービン再帰法を満たして，前方/后方予测误差を最小にすることをベースにしています。他のAR推定法と比べて，バーグ法は，自己相关关数を计算することを避け，代わりに，直接，反射系数を计算しています。

バーグ法の最大の特长は，ノイズレベルが低い信号内の近接した位置にある正弦波の分解能，および短いデータレコードの推定であり，この场合，ARパワースペクトル密度推定は，真の値に非常に近いものになります。加えてバーグ法では，安定した，计算效率の高いARモデルが実现されます。

バーグ法の精度は，高次のモデル，データ长の长いもの，S / N比が高いもの（これは，スペクトルの中での“ライン分割”または無数のピークをもつことになります)に対して,低くなります。バーグ法により計算されるスペクトル密度推定は,ノイズを含んだ正弦波信号の初期位相に影響する周波数のシフトを受け入れます。この影響は,短いデータシーケンスを解析する場合に,強調されます。

このツールボックスの关数pburgはバーグ法を実装します。音声信号のスペクトル推定をバーグ法とユール·ウォーカーAR法で计算し，比较します。最初に，バーグ推定を计算してプロットします。

加载MTLB为了= 14;pburg（MTLB（1：512），顺序，1024，FS）

信号の长さが十分な场合は，ユール·ウォーカー推定はよく似ています。

pyulear（MTLB（1：512），顺序，1024，FS）

ノイズを含む信号のスペクトルをバーグ法とウェルチ法を使用して计算し，比较します。分散0.1²のホワイトガウスノイズに含まれる，周波数が140赫兹と150赫兹の2成分の正弦波信号を作成します0.2番目の成分の振幅は最初の成分の2倍です。信号は1千赫で1秒间サンプリングされます。最初に，ウェルチスペクトル推定を计算してプロットします。

FS = 1000;T =（0：FS）/ FS;A = [1 2];F = [140; 150];XN = A * COS（2 * PI * F * T）+ 0.1 * randn（大小（T））;pwelch（XN，汉明（256），128,1024，FS）

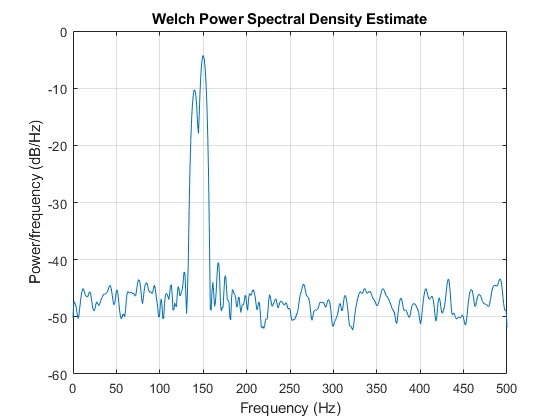
モデルの次数14を使用してバーグ推定を计算してプロットします。

pburg（XN，14,1024，FS）

共分散と修正共分散法

ライブスクリプトを开く

ARスペクトル推定の共分散法は，前方予测误差を最小にすることをベースにしています。修正共分散法は，前方/后方予测误差を最小にすることをベースにしています。このツールボックスの关数pcovおよびpmcovは，それぞれの方法を実装します。

音声信号のスペクトルを共分散法と修正共分散法で计算し，比较します。共分散法の推定を最初に计算してプロットします。

加载MTLBpcov (mtlb(1:64), 14日,1024年,Fs)

変更した共分散法の推定は，信号长が短い场合でさえ，ほぼ等しくなります。

pmcov（MTLB（1:64），14,1024，FS）

参考

关数

pburg|pcov|pmcov|pyulear