在优化中提高准确性和性能

打开生活的脚本

此示例演示了符号数学工具箱有助于最小化求解非线性系统的方程式时的错误。

这个例子使用了以下的符号数学工具箱功能:

计算分析梯度使用坡度
计算解析雅可比矩阵使用雅各比亚
将符号结果转换为数字函数matlabFunction
分析可视化与fplot

目标是找到最小值函数。，或所谓的“香蕉”功能。

$F （ X 的） = {σ.}_{一世 = 1}^{N. / 2} 1 0. 0. （ X_{2 一世} - X_{2 一世 - 1}^{2} {的）}^{2} + （ 1 - X_{2 一世 - 1} {的）}^{2}$

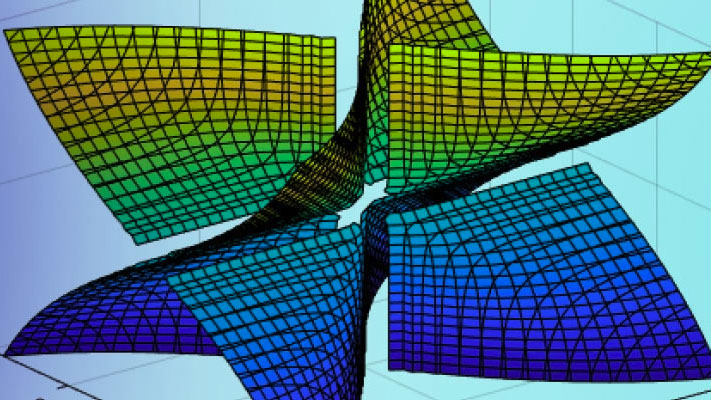
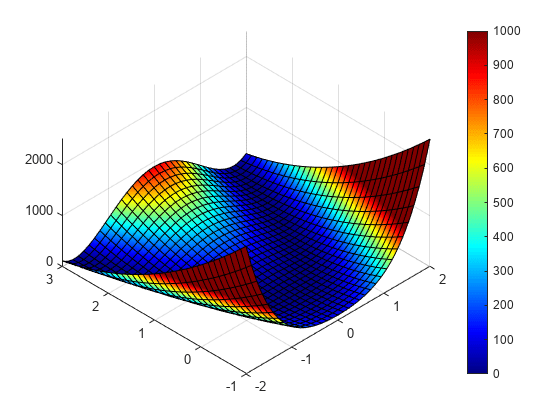
使用fplot创建两个变量的RosenBrock函数的快速可视化

纽带Xy= 1;b = 100;f (x, y) = (ax) ^ 2 + b * (x ^ 2) ^ 2

f (x, y) =
                 ${(X - 1)}^{2} + One hundred. {(y - X^{2})}^{2}$

FSURF（F，[ -  2 2 -1 3]）视图（[ -  45 50]）Colormap喷射Caxis（[0,1000]）彩色键

图中包含一个轴对象。axis对象包含一个函数曲面类型的对象。

动机

这具有解析雅可比矩阵的非线性方程优化工具箱中的示例通过使用该工具盒解决了相同的问题fsolve函数。该示例中显示的工作流有两个潜在的错误来源。你需要

从文本中的数学形式转换RosenBrock函数和雅各比亚的方程式到数字代码。
明确地计算雅匹碧。对于复杂的方程式，此任务易于错误。

这个例子表明，使用符号数学来描述问题陈述和随后的步骤可以最小化甚至消除此类错误。

将Rosenbrock函数重写为非线性方程组

首先，转换Rosenbrock函数F到非线性方程系统F,在那里F是一个梯度F．

清除n = 64;x = sym（“x”，[n，1]）;f = sum（100 *（x（2：2：n）-x（1：2：n）。^ 2）。^ 2 +（1-x（1：2：n））。^ 2）;f =梯度（f，x）;

展示前10个方程:

F (1:10)

ans =
                 
                   $（ \begin{array}{c} 2 X_{1} - 400 X_{1} (X_{2} - {X_{1}}^{2}) - 2 \\ 200 X_{2} - 200 {X_{1}}^{2} \\ 2 X_{3.} - 400 X_{3.} (X_{4.} - {X_{3.}}^{2}) - 2 \\ 200 X_{4.} - 200 {X_{3.}}^{2} \\ 2 X_{5.} - 400 X_{5.} (X_{6.} - {X_{5.}}^{2}) - 2 \\ 200 X_{6.} - 200 {X_{5.}}^{2} \\ 2 X_{7.} - 400 X_{7.} (X_{8.} - {X_{7.}}^{2}) - 2 \\ 200 X_{8.} - 200 {X_{7.}}^{2} \\ 2 X_{9.} - 400 X_{9.} (X_{10.} - {X_{9.}}^{2}) - 2 \\ 200 X_{10.} - 200 {X_{9.}}^{2} \end{array} 的）$

以匹配优化工具箱中显示的中间结果例子，使用相同的形式F．

F (1:2: n) =简化(F (1:2: n) + 2 * x (1:2: n)。* F (2:2: n));F (1:2: n) = - F (1:2: n) / 2;(2:2: n) = F (2:2: n) / 20;

现在方程组是相同的:

F (1:10)

ans =
                 
                   $（ \begin{array}{c} 1 - X_{1} \\ 10. X_{2} - 10. {X_{1}}^{2} \\ 1 - X_{3.} \\ 10. X_{4.} - 10. {X_{3.}}^{2} \\ 1 - X_{5.} \\ 10. X_{6.} - 10. {X_{5.}}^{2} \\ 1 - X_{7.} \\ 10. X_{8.} - 10. {X_{7.}}^{2} \\ 1 - X_{9.} \\ 10. X_{10.} - 10. {X_{9.}}^{2} \end{array} 的）$

计算表示方程组的矩阵雅可比矩阵

使用雅各比亚计算雅各的雅各斯F．该函数象征性地计算雅可碧展妇女，从而避免与衍生物的数值近似相关的错误。

摩根富林明=雅可比矩阵(F (x);

显示Jacobian矩阵的前10行和列。

摩根富林明(1:10,1:10)

ans =
                 
                   $（ \begin{array}{c} - 1 & 0. & 0. & 0. & 0. & 0. & 0. & 0. & 0. & 0. \\ - 20. X_{1} & 10. & 0. & 0. & 0. & 0. & 0. & 0. & 0. & 0. \\ 0. & 0. & - 1 & 0. & 0. & 0. & 0. & 0. & 0. & 0. \\ 0. & 0. & - 20. X_{3.} & 10. & 0. & 0. & 0. & 0. & 0. & 0. \\ 0. & 0. & 0. & 0. & - 1 & 0. & 0. & 0. & 0. & 0. \\ 0. & 0. & 0. & 0. & - 20. X_{5.} & 10. & 0. & 0. & 0. & 0. \\ 0. & 0. & 0. & 0. & 0. & 0. & - 1 & 0. & 0. & 0. \\ 0. & 0. & 0. & 0. & 0. & 0. & - 20. X_{7.} & 10. & 0. & 0. \\ 0. & 0. & 0. & 0. & 0. & 0. & 0. & 0. & - 1 & 0. \\ 0. & 0. & 0. & 0. & 0. & 0. & 0. & 0. & - 20. X_{9.} & 10. \end{array} 的）$

大多数雅各比亚矩阵的元素摩根富林明是0。然而，当你把这个矩阵转换成amatlabFunction，结果是一个密集的数值矩阵。通常，在稀疏矩阵上的操作比在密集矩阵上的操作更有效。

因此，要创建高效的代码，只需转换摩根富林明在调用之前到符号矢量matlabFunction．是和js代表稀疏模式摩根富林明．

[是，js] =查找（jf）;jf = jf（jf〜= 0）;

将方程组和雅可比矩阵转换为MATLAB函数

方程组F代表RosenBrock函数的是一个由符号表达式组成的符号矩阵。能够用它来解决fsolve函数，将该系统转换为MATLAB函数．在这一步，转换两者是很方便的F及其雅可比矩阵,摩根富林明，为一个基于文件的MATLAB函数，FJFfun．原则上，这允许F和摩根富林明重用变量。或者，您可以将它们转换为单个MATLAB函数。

matlabfunction（[f; jf]，'var', x,'文件'那“FJFfun”）;

FJFfun接受列表形式的变量，但是fsolve期待变量矢量。功能genericObj将向量转换为列表。匿名功能Bananaobj.定义为修复参数值genericObj．注意在功能中使用稀疏性模式genericObj．进一步注意这种方法的使用FJFfun和genericObj一起与所代表的特定表达式联系在一起F并且可以用作任何F．

Bananaobj = @（y）genericobj（y，@ fjffun，是，js）

Bananaobj =function_handle具有值：@ (y) genericObj (y, @FJFfun, js)

使用`fsolve`在数字上解决非线性方程系统

使用fsolve对于方程式，转换为MATLAB函数。使用起点x（i）= -1.9对于奇指标，和x (i) = 2对于偶数项。放“显示”到'iter'看到求解器的进步。放'雅各比亚'到'在'使用jacobian定义Bananaobj.．

X0（1：N，1）= -1.9;X0（2：2：n，1）= 2;选项= Optimoptions（@fsolve，“显示”那'iter'那'雅各比亚'那'在'）;[Sol1，FSOL，EXITFLAG，输出，Jac] = FSOLVE（Bananaobj，X0，选项）;

一阶信任区域迭代Func-count f（x）步骤最优性半径0 1 8563.84 615 11 11 2 3093.71 11 329 11 2 3 225.12 2.5 34.8 2.5 3 4 212.48 6.25 325 3 4 212.48 6.25 34.1 6.25 4 5 212.48 6.25 34.25 5 6212.48 1.5625 34.1 1.56 6 7 116.793 0.390625 5.79 0.391 7 8 109.947 0.390625 0.753 0.391 8 9 99.4696 0.976563 1.2 0.977 9 10 83.6416 2.44141 7.13 2.44 10 11 77.7663 2.44141 9.94 2.44 11 12 77.7663 2.44141 9.94 2.44 12 13 43.013 0.610352 1.38 0.61 13 14 36.4334 0.6103521.58 0.61 14 15 34.1448 1.52588 6.71 1.53 15 16 18.0108 1.52588 4.91 1.53 16 17 8.48336 1.52588 3.74 1.53 17 18 3.74566 1.52588 3.58 1.53 18 19 1.46166 1.52588 3.32 1.53 19 20 0.29997 1.24265 1.94 1.53 20 21 0 0 0.0547695 1.53方程求解。FSOLVE完成，因为通过函数容差的值测量，功能值的向量接近零，并且通过梯度测量的问题显示问题。

用vpasolve对非线性方程组进行数值求解

非线性方程组，F，也可以用vpasolve函数，这是一个可在符号数学工具箱中使用的数值求解器。两者的关键区别vpasolve和fsolve就是它fsolve用双精度算法来解方程，然而vpasolve使用可变精度算术，因此，可以控制计算的准确性。

sol2 = vpasolve (F);

如果你把方程组的解赋给一个变量，sol2.，然后vpasolve以结构数组的形式返回解决金宝搏官方网站方案。你可以访问每个解决方案(结构数组的每个字段):

sol2.x1

ans =
                  $1．0$

你也可以转换sol2.到符号矢量，然后访问一系列解决方案。金宝搏官方网站例如，显示第5到第25个解决方案：金宝搏官方网站

为了(1) sol2_array(K) = sol2.(char(x(K)));结尾sol2_array (25)

ans =
                  $（ \begin{array}{c} 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 & 1．0 \end{array} 的）$

辅助函数

函数F [J] = genericObj (x, FJFfun, js)％genericobj用作输入，矢量x，函数和雅各比人评估％函数处理fjffun，稀疏模式是，js和返回作为输出，％函数和jacobian的数值：f和jfunction% FJs(1:length(x))是函数的数字向量% FJs(length(x)+1:end)是雅可比矩阵非零项的数值向量伊势亚= num2cell (x);fj = FJFfun(伊势亚{:});F = fj(1:长度(x));J =稀疏(js, fj(长度(x) + 1:结束));结尾

在优化中提高准确性和性能

动机

将Rosenbrock函数重写为非线性方程组

计算表示方程组的矩阵雅可比矩阵

将方程组和雅可比矩阵转换为MATLAB函数

使用`fsolve`在数字上解决非线性方程系统

用vpasolve对非线性方程组进行数值求解

辅助函数

符号数学工具箱文档

金宝app

数学建模与符号数学工具箱

在优化中提高准确性和性能

动机

将Rosenbrock函数重写为非线性方程组

计算表示方程组的矩阵雅可比矩阵

将方程组和雅可比矩阵转换为MATLAB函数

使用fsolve在数字上解决非线性方程系统

用vpasolve对非线性方程组进行数值求解

辅助函数

符号数学工具箱文档

金宝app

数学建模与符号数学工具箱

使用`fsolve`在数字上解决非线性方程系统