非线性数据配件
这个例子展示了如何使用几个Optimization Toolbox™算法将非线性函数拟合到数据中。
问题的设置
考虑以下数据:
数据=...[0.0000 5.8955 0.1000 3.5639 0.2000 2.5173 0.3000 1.9790 0.4000 1.8990 0.5000 1.3938 0.6000 1.1359 0.7000 1.0096 0.8000 1.0343 0.9000 0.8435 1.0000 0.6856 1.1000 0.6100 1.2000 0.5392 1.3000 0.3946 1.4000 0.3903 1.5000 0.5474 1.6000 0.3459 1.7000 0.1370 1.8000 0.2211 1.9000 0.1704 2.0000 0.2636];
让我们绘制这些数据点。
t =数据(:1);y =数据(:,2);%轴([0 2 -0.5 6])%坚持绘图(t,y,“罗”)标题('数据点')
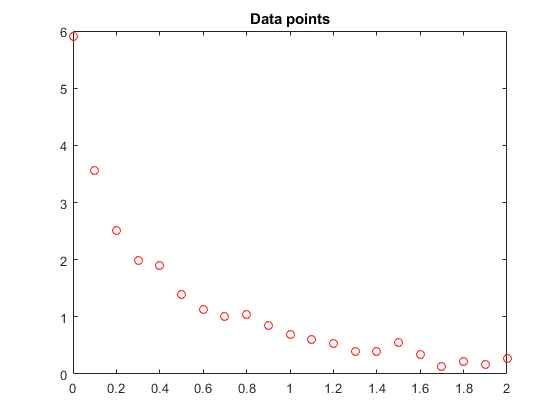
%推迟
我们想要符合这个函数
Y = C(1)* exp( - - - 1)* T)+ C(2)* EXP( - - - 2)* T)
到数据。
解决方案方法使用lsqcurvefit
的lsqcurvefit函数很容易解决这类问题。
首先,根据一个变量X定义参数:
X(1)= C(1)
X(2)=林(1)
X(3)= C(2)
林x (4) = (2)
然后将曲线定义为参数x和数据t的函数:
f = @(x,xdata)x(1)* exp(-x(2)* xdata)+ x(3)* exp(-x(4)* xdata);
我们任意设置初始点x0如下:c(1) = 1, lam(1) = 1, c(2) = 1, lam(2) = 0:
X0 = [1 1 1 0];
我们运行求解器并绘制得到的合身。
[x,Resnorm,〜,EXITFLAG,输出] = LSQCurveFit(F,X0,T,Y)
局部最小值。Lsqcurvefit停止是因为相对于初始值的平方和的最终变化小于函数公差的值。
x =1×43.0068 10.5869 2.8891 1.4003
resnorm = 0.1477
ExitFlag = 3.
输出=结构与字段:Firstorderopt:7.8852E-06迭代:6 Funccount:35 Cgiteration:0算法:'信任区域 - 反光'STAPEIZE:0.0096消息:'...'
持有上绘图(t,f(x,t))保持关闭
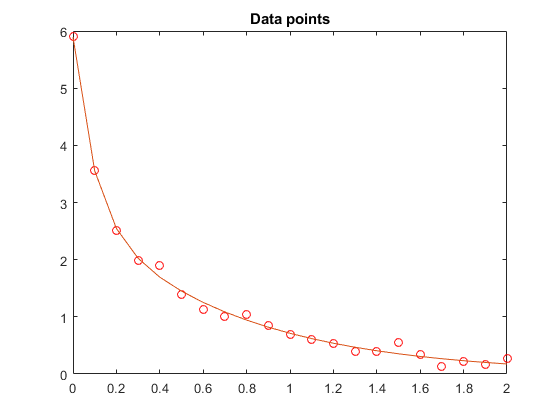
解决方案方法使用fminunc
使用解决问题fminunc,我们设目标函数为残差平方和。
fsumsquares = @(x)和((f(x,t) - y)。^ 2);opts = Optimoptions(“fminunc”,'算法','quasi-newton');[xunc, ressquared eflag outputu] =...Fminunc(fsumsquares,x0,选择)
局部最小值。由于梯度的大小小于最优性公差的值,优化完成。
xunc =1×42.8890 1.4003 3.0069 10.5862
ressquared = 0.1477
eflag = 1
Outputu =结构与字段:迭代:30 Funccount:185 STAPEIZE:0.0017 LSSTeplenth:1:1 FirstOrderopt:2.9662E-05算法:'Quasi-Newton'消息:'...'
注意fminunc找到了相同的解lsqcurvefit,但需要进行更多的函数计算。的参数fminunc与那些相反的顺序lsqcurvefit;较大的lam是lam(2),而不是lam(1)。这并不奇怪,变量的顺序是任意的。
fprintf([“使用fminunc,”有%d迭代,“...'和%d使用lsqcurvefit。\ n'],...OutputU.Iltations,Output.Iltations)
使用fminunc进行了30次迭代,使用lsqcurvefit进行了6次迭代。
fprintf([“使用fminunc,”有%d函数评估“...'和%d使用lsqcurvefit。'],...outputu.funccount,output.funccount)
使用Fminunc和35使用LSQCurveFit有185个功能评估。
线性和非线性问题的分裂
请注意,拟合问题是参数C(1)和C(2)中的线性。这对于任何LAM(1)和LAM(2)的值,我们可以使用反斜杠运算符来找到解决最小二乘问题的C(1)和C(2)的值。
我们现在将问题重新建立为二维问题,搜索Lam(1)和Lam(2)的最佳值。如上所述,在每个步骤中在每个步骤中计算C(1)和C(2)的值。
typefitvector
function yEst = fitvector(lam,xdata,ydata) % fitvector DATDEMO用于返回拟合函数值。% yEst = FITVECTOR(lam,xdata)返回在参数设置为lam的数据点xdata处的拟合函数y %(定义如下)的值。% yes作为一个N乘1的列向量返回,其中N是%数据点的数量。% % FITVECTOR假设拟合函数y的形式为% % y = c(1)*exp(-lam(1)*t) +…+ c(n)*exp(-lam(n)*t) % %, n个线性参数c, n个非线性参数lam。为了求解线性参数c,我们构建一个矩阵a %,其中a的第j列是exp(-lam(j)*xdata) (xdata是一个向量)。然后我们求解线性最小二乘解c, %,其中ydata是y的观测值,A = 0 (length(xdata),length(lam));% build A matrix for j = 1:length(lam) A(:,j) = exp(-lam(j)*xdata);end c = A\ydata;%解A*c = y为线性参数c % return the estimated response based on c
使用方法解决问题lsqcurvefit,从二维初始点lam(1), lam(2)出发:
X02 = [1 0];F2 = @(x,t) fitvector(x,t,y);(x2, resnorm2, ~, exitflag2 output2] = lsqcurvefit (F2, x02 t y)
局部最小值。Lsqcurvefit停止是因为相对于初始值的平方和的最终变化小于函数公差的值。
x2 =1×210.5861 1.4003
Resnorm2 = 0.1477.
exitflag2 = 3
output2 =结构与字段:firstorderopt: 4.4018e-06 iterations: 10 funcCount: 33 cgiterations: 0 algorithm: 'trust-region- reflection ' stepsize: 0.0080 message: '…'
二维解决方案的效率类似于四维解决方案的效率:
fprintf([“使用2-D”有%D函数评估...“配方,使用4-D配方的%D.”],...Output2.Funccount,Output.funccount)
使用二维配方进行了33项功能评估,使用4d配方进行了35项功能评估。
分割问题比初始猜想更健壮
为原来的四参数问题选择一个错误的起点会导致一个不是全局的局部解。对于分裂二参数问题,选择一个具有相同坏lam(1)和lam(2)值的起始点可以得到全局解。为了证明这一点,我们重新运行初始问题,初始问题会导致一个相对较差的局部解决方案,并将结果与全局解决方案进行比较。
X0bad = [5 1 1 0];[xbad, resnormbad, ~, exitflagbad outputbad] =...lsqcurvefit(f,x0bad,t,y)
局部最小值。Lsqcurvefit停止是因为相对于初始值的平方和的最终变化小于函数公差的值。
XBAD =1×4-22.9036 2.4792 28.0273 2.4791
resnormbad = 2.2173
ExitFlagbad = 3.
outputbad =结构与字段:FirstOrderopt:0.0057迭代:32 Funccount:165 Cgiterations:0算法:'信任区域反光'步骤:0.0021消息:'...'
持有上绘图(t,f(xbad,t),'G')传说('数据',“全球健康”,'糟糕的地方合身','位置','ne'抱紧关闭
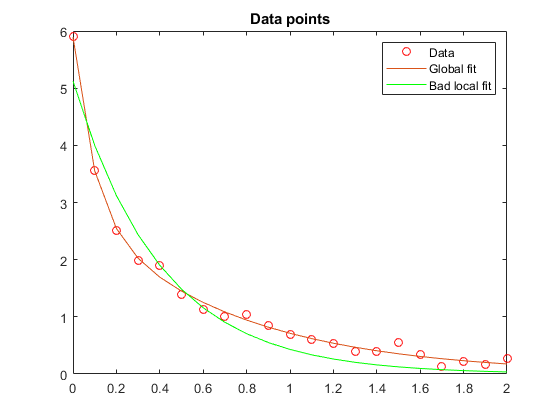
fprintf(["好的结束点的剩余标准是%f "...'坏结局点的残余标准是%f。'],...Resnorm,ResnorMBAD)
良好结束点处的残余规范为0.147723,坏终点处的残余规范为2.217300。

