在过去的一个月里，我一直在使用我描述的可变格式16位浮点运算gydF4y2Ba在这篇文章中gydF4y2Ba．这是一项令人沮丧的工作。我发现有限的精度和有限的半精度范围使得它几乎不能用于我喜欢做的矩阵计算实验。在这篇文章中，我将描述其中的一些实验。gydF4y2Ba

我并不是说半精度浮点是没有用的。包括英特尔和谷歌在内的组织都采用了IEEE 754标准gydF4y2Bafp16gydF4y2Ba和新gydF4y2Babfloat16gydF4y2Ba机器学习和图像处理的工作格式，gydF4y2Ba链接gydF4y2Ba．我只是不建议通用工程和科学计算使用这两种格式。gydF4y2Ba

内容gydF4y2Ba

vfp16gydF4y2Ba

我已经修改了gydF4y2Ba帮助gydF4y2Ba输入我的变量格式半精度对象。这是更新的版本。gydF4y2Ba

医生gydF4y2Bavfp16gydF4y2Ba

以下是当前可用的功能列表。正如您所看到的，这远离完整的集合。主函数gydF4y2Ba莫德利维gydF4y2Ba（反斜杠），gydF4y2Ba陆gydF4y2Ba,gydF4y2BaQR.gydF4y2Ba和gydF4y2BaSVD.gydF4y2Ba是可行的，但我还没有做过任何关于复杂算术的事情，所以gydF4y2BaeiggydF4y2Ba不在列表中。gydF4y2Ba

方法(vfp16)gydF4y2Ba

陆方法类vfp16: abs修复+单小二进制ge马克斯权力大小下三角阵ctranspose gt -精密sqrt triu诊断接头十六进制mldivide qr subsasgn使用uint disp horzcat mrdivide最大浮点数subsindex uminus显示isfinite mtimes最小正浮点数subsref vertcat双le ne rem和vfp16 eps log2标准圆的圣言eq lt次包装标志gydF4y2Ba

vfp16解剖学gydF4y2Ba

这是我在我以前的帖子中的图表重复，除了现在我正在使用gydF4y2Bavfp16gydF4y2Ba对象本身来计算参数。gydF4y2Ba

disp (gydF4y2Ba' p eps realmax realmin tiny'gydF4y2Ba）gydF4y2Ba为gydF4y2BaP = 1:15 vfp16(gydF4y2Ba“精度”gydF4y2Ba，p) x = vfp16(1);Y = [eps(x) realmax(x) realmin(x) tiny(x)];流(gydF4y2Ba'%4d %12.4g %12.4g %12.4g\n'gydF4y2Ba、磷、双(y))gydF4y2Ba结束gydF4y2Ba

P EPS REALMAX TEALMIN TINAMIN 1 0.5 INF 0 0 2 0.25 INF 0 0 3 0.125 INF 0 0 4 0.0625 1.742C + 308 2.225E-308 1.391E-309 5 0.03125 1.32E + 154 2.983E-154 9.323E-156 6 0.015631.149E + 77 3.454E-77 5.398E-79 7 0.007813 3.39E + 38 1.175E-38 9.184E-41 8 0.003906 1.841E + 19 2.168E-19 8.47E-22 9 0.001953 4.291CE + 09 9.313E-101.819E-12 10 0.0009766 6.55E + 04 6.104E-05 5.96E-08 11 0.00048832.015.9 0.01563 7.629C-06 12 0.0002441 16 0.25 6.104411 0.0001221 4 1 0.0001221 4 1 0.0001221 14 0 2 INF 0.0001221 15 0 4 -0 0.0001221gydF4y2Ba

对于等于1,2或3的精度，有12位或更多位致力于指数等等gydF4y2Ba最大浮点数gydF4y2Ba,gydF4y2Ba最小正浮点数gydF4y2Ba和gydF4y2Ba小gydF4y2Ba不能用MATLAB的常规双精度算法来表示gydF4y2Bavfp16gydF4y2Ba不能利用扩展范围。gydF4y2Ba

另一方面，对于等于或大于11的精度，gydF4y2Ba每股收益gydF4y2Ba小于gydF4y2Ba最小正浮点数gydF4y2Ba，所以底流而不是舍入决定了精度。特别是如果潜流逐渐gydF4y2Ba从gydF4y2Ba在美国，具有这种精度的计算表现不佳。因此我一直gydF4y2BapgydF4y2Ba在范围内gydF4y2Ba4 . <= p <= 10gydF4y2Ba．gydF4y2Ba

逐渐下溢gydF4y2Ba

在我们有IEEE标准之前，可移植到不同架构的代码必须发现机器的准确性。其中一种方法涉及以下计算。让我们用标准gydF4y2Bafp16gydF4y2Ba其中有gydF4y2Bap = 10.gydF4y2Ba和gydF4y2Ba“弱智者”gydF4y2Ba转gydF4y2Ba“上”gydF4y2Ba．gydF4y2Ba

格式gydF4y2Ba短gydF4y2BaVFP16（gydF4y2Ba“fp16”gydF4y2Ba) a = vfp16(4)/vfp16(3) b = a-1 c = b+b+b e = 1-cgydF4y2Ba

A = 1.3330 b = 0.3330 c = 0.9990 e = 9.7656e-04gydF4y2Ba

用精确算法,gydF4y2BabgydF4y2Ba将是1/3，gydF4y2BacgydF4y2Ba是1，然后呢gydF4y2BaegydF4y2Ba将是零。但是，除非我们用的是三进制计算机，否则除法3时肯定会有舍入误差。这是唯一的舍入误差。所以gydF4y2BabgydF4y2Ba不是确切的1/3，gydF4y2BacgydF4y2Ba不完全是1，而且gydF4y2BaegydF4y2Ba等于漂浮数的间距，但大于1.0。换句话说，gydF4y2BaegydF4y2Ba等于gydF4y2Ba每股收益(1)gydF4y2Ba．gydF4y2Ba

让我们再次使用等于11的精确度，逐渐下溢。gydF4y2Ba

VFP16（gydF4y2Ba“精度”gydF4y2Ba，11，gydF4y2Ba“弱智者”gydF4y2Ba,gydF4y2Ba“关闭”gydF4y2Ba) a = vfp16(4)/vfp16(3) b = a-1 c = b+b+b e = 1-cgydF4y2Ba

a = 1.3335 b = 0.3335 c = 1.0005 e = 0gydF4y2Ba

现在除以3是向上四舍五入而不是向下gydF4y2BacgydF4y2Ba略大于一个，但计算gydF4y2BaegydF4y2Ba溢出并刷新为零。这是一个简单的例子，但它展示了在指数范围有限的时候逐渐下溢的重要性。gydF4y2Ba

融合乘以补充gydF4y2Ba

融合乘加在残差的舍入误差上只产生很小的差异gydF4y2BaRgydF4y2Ba从随机10×10矩阵的Lu分解，按数量的非系统测量gydF4y2BaRgydF4y2Ba．gydF4y2Ba

VFP16（gydF4y2Ba“弱智者”gydF4y2Ba,gydF4y2Ba“上”gydF4y2Ba）形式= {gydF4y2Ba“fp16”gydF4y2Ba,gydF4y2Ba'bfloat16'gydF4y2Ba};菲利普-马萨= {gydF4y2Ba“关闭”gydF4y2Ba,gydF4y2Ba“上”gydF4y2Ba};rng (17)gydF4y2Ba为gydF4y2Bavfp16 = 1:2 vfp16(form{j}) A = vfp16(randn(10,10));gydF4y2Ba为gydF4y2BaK = 1:2 vfp16(gydF4y2Ba'fma'gydF4y2Ba，fma{k}) [L,U,p] = lu(A);R = L*U - A(p，:);次要情节(2,2,2 * (j - 1) + k)间谍(双(R))标题([形式{j}gydF4y2Ba”,菲利普-马萨”gydF4y2Ba菲利普-马萨{k}])gydF4y2Ba结束gydF4y2Ba结束gydF4y2BaVFP16（gydF4y2Ba“弱智者”gydF4y2Ba,gydF4y2Ba“上”gydF4y2Ba）gydF4y2Ba

列旋转的QR，弗兰克矩阵gydF4y2Ba

Frank矩阵$F_n$是一个有趣的测试矩阵。这是F_6美元。gydF4y2Ba

F6 =画廊（gydF4y2Ba“弗兰克”gydF4y2Ba6)gydF4y2Ba

F6 = 6 5 4 3 2 11 5 5 4 3 2 1 0 4 4 3 2 1 0 0 3 3 2 1 0 0 0 2 2 1 0 0 0 0 1 1gydF4y2Ba

我们将使用列枢转计算QR分解，并查看$ r_n $，$ r $的最后一个对角线元素。事实证明，$ F_N $靠近RANK $ N-1 $的矩阵，并且预测$ r_n $腐烂至零指数为$ n $ changes。这是$ f_6 $的qr分解的$ r $;您可以看到最后一个对角线元素中指数小的开始。gydF4y2Ba

[Q, R E] = qr (F6);RgydF4y2Ba

R = -8.1240 -6.7700 -5.1698 -6.8931 -3.4466 -1.7233 0 -3.8944 0.5136 0.6847 0.3424 0.1712 00 3.6068 2.4986 2.7742 1.3871 000 -1.6652 0.5547 0.2773 000 1.0001 1.0000 0000 0.0053gydF4y2Ba

当通过我们的半精度算术计算QR分解时，对于长时间，不能跟踪该指数衰减。在以下对数绘制的黑线是$ r_n $。另一条线是用的值gydF4y2Bavfp16gydF4y2Ba变精度算法。虽然$r_{15}$小于$10^{-10}$，但其他值都不小于$10^{-4}$。gydF4y2Ba

虚线是由精确的零引起的，不能在对数图上画出来。gydF4y2Ba

Rn = 0(1、15);rn = 0(10、15);gydF4y2Ba为gydF4y2Ban = 1:15 A = gallery(gydF4y2Ba“弗兰克”gydF4y2Ba，n）;[〜，r，e] = qr（a）;rn（n）= r（n，n）;gydF4y2Ba为gydF4y2BaP = 4:10 vfp16(gydF4y2Ba“精度”gydF4y2Ba，p) X = vfp16(A);[〜，r，e] = qrp（x）;RN（p，n）= r（n，n）;gydF4y2Ba结束gydF4y2Ba结束gydF4y2Baxqrp_print xqrp_plotgydF4y2Ba

N 2 3 4…13 14 15 Rn 4.47e-01 2.43e-01 -9.41e-02…-1.41e-09 1.09e-10 -7.82e-12 rn p 4 -0.4375 -0.2813 0.0547…-0.0547 -0.1875 -0.1406 5 -0.4844 -0.2969 0.0977…- - - - - - - - - - - --0.4453 -0.2402 0.1016…-0.4434 -0.2402 0.0879…-0.0118 0.0000 0.0000 9 -0.4473 -0.2412 0.0879…-0.0020 0.0000 -0.0039 10 -0.4468 -0.2429 0.0952…-0.0039 -0.0039 0.0000gydF4y2Ba

SVD，希尔伯特矩阵gydF4y2Ba

现在，对于这篇博客的读者所熟悉的两个玩家，gydF4y2Ba希尔伯特矩阵gydF4y2Ba和gydF4y2Ba奇异值分解gydF4y2Ba．这是H_5美元。gydF4y2Ba

格式gydF4y2Ba老鼠gydF4y2BaH5 = hilb (5)gydF4y2Ba

H5 = 1/2 1/3 1/3 1/4 1/4 1/2 1/2 1/2 1/3 1/4 1/5 1/6 1/6 1/3 1/4 1/5 1/6 1/7 1/7 1/7 1/4 1/7 1/45 1/6 1/7 1/8 1/8 1/5 1/6 1/7 1/7 1/8 1/8 1/8gydF4y2Ba

这个矩阵是对称的，正定的，所以它的奇异值等于它的特征值。看看奇异值$H_6$是如何迅速衰减的。gydF4y2Ba

格式gydF4y2Ba短gydF4y2BaggydF4y2Ba到H6 = hilb (6);sigma6 =圣言(编辑)gydF4y2Ba

Sigma6 = 1.6189 0.24236 0.016322 0.00061575 1.2571e-05 1.0828e-07gydF4y2Ba

该实验就像坦率矩阵的QR，除了最小奇异值的对数图几乎是完全线性的并且具有陡峭的斜率。您可以看到来自IEEE标准的红线与p = 10是跟踪$ \ sigma_n $的最佳作业。gydF4y2Ba

Sn =零（10,13）;gydF4y2Ba为gydF4y2Ban = 2:13 A = hilb(n)S =圣言();Sn（n）= s（n）;gydF4y2Ba为gydF4y2BaP = 4:10 vfp16(gydF4y2Ba“精度”gydF4y2Ba，p) X = vfp16(A);s =圣言(X);sn (p, n) = s (n);gydF4y2Ba结束gydF4y2Ba结束gydF4y2Baxsvd_hilbert_print xsvd_hilbert_plotgydF4y2Ba

N 2 3 4…11 12 13 Sn 6.57e-02 2.69e-03 9.67e-05…3.40e-15 1.11e-16 3.79e-18 sn p 4 6.99e-02 4.81e-03 1.89e-03…4.44e-04 2.11e-04 3.13e-04 5 6.91e-02 1.90e-03 2.24e-03…2.20e-04 2.05e-04 5.45e-05 6 6.56e-02 2.36e-03 0.00e+00…1.18e-04 2.44e-05 1.33e-04 7 6.72e-02 3.09e-03 9.89e-05…1.22e-04 1.70e-05 6.97e-05 8 6.46e-02 2.79e-03 1.74e-04…4.46e-05 2.36e-05 2.43e-05 9 6.59e-02 2.91e-03 3.12e-05…6.55e-02 2.61e-03 3.67e-05…3.45 8.26 9.33 e-07 e-06 e-06gydF4y2Ba

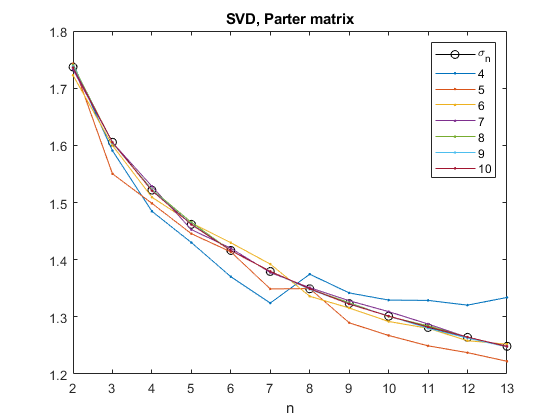
圣言,合伙人矩阵gydF4y2Ba

现在有所不同。我讨论了这个画廊叫什么gydF4y2Ba合伙人矩阵gydF4y2Ba五年前。这是$ p_5 $。gydF4y2Ba

格式gydF4y2Ba老鼠gydF4y2BaP5 =画廊(gydF4y2Ba'parter'gydF4y2Ba5)gydF4y2Ba

P5 = 2 -2 -2/3 -2/ 2 - 5 -2/7 2/3 -2/ 2 -2/3 -2/ 2/5 2/5 2/9 2/7 2/5 2/5 2/ 2gydF4y2Ba

大多数奇异值都收敛到$\pi$。我不确定最小的奇异值在哪里，但它肯定不会在指数上为零。现在计算gydF4y2Bavfp16gydF4y2Ba随着范围内的任何精度gydF4y2Ba4 . <= p <= 10gydF4y2Ba做得很好。gydF4y2Ba

Sn =零（1,13）;Sn =零（10,13）;gydF4y2Ba为gydF4y2Ban = 2:13 a =图库（gydF4y2Ba'parter'gydF4y2Ba，n）;s = svd（a）;Sn（n）= s（n）;gydF4y2Ba为gydF4y2BaP = 4:10 vfp16(gydF4y2Ba“精度”gydF4y2Ba，p) X = vfp16(A);s =圣言(X);sn (p, n) = s (n);gydF4y2Ba结束gydF4y2Ba结束gydF4y2Baxsvd_parter_print xsvd_parter_plotgydF4y2Ba

n 2 3 4 ... 11 12 13 43 4.7370 1.6.2814 1.5217 ... 1.2814 1.2640 1.2485 Sn P 4 1.7430 1.5907 1.4846 1.1.3287 1.3204 1.3339 5 1.7430 1.5502 1.4985 1.2493 1.2373 1.2223 6 1.7227 1.5997 1.5093 ... 1.27991.2582 1.2521 7 1.7327 1.5283 1.2874 1.2874 1.2488 1.7407 1.6.2843 1.5229 ... 1.2843 1.2641 1.2478 9 1.7380 1.6040 1.5216 1.2799 1.2799 1.279 1.7361 1.6051 1.5206 1.1.2822 1.2646 1.2822 1.2646 1.2479gydF4y2Ba

克里夫的实验室gydF4y2Ba

我将会更新gydF4y2BaCleve_s实验室gydF4y2Ba在MATLAB中央文件交换到版本4.30，包括我的更改gydF4y2Ba@ vfp16.gydF4y2Ba．gydF4y2Ba

获取matlab代码gydF4y2Ba

发布与MATLAB®R2018bgydF4y2Ba