广义极值分布- MATLAB和Simulink - MathWorks澳大利亚金宝app - 金宝app,下载188bet金宝搏,金宝搏官方网站

广义极值分布

定义

广义极值分布的概率密度函数具有位置参数µ、尺度参数σ和形状参数k≠0是

$y ＝ f （ x | k ， μ ， σ ）＝（ \frac{1}{σ} ）经验值（ - {（ 1 + k \frac{（ x - μ ）}{σ} ）}^{- \frac{1}{k}} ） {（ 1 + k \frac{（ x - μ ）}{σ} ）}^{- 1 - \frac{1}{k}}$

为

$1 + k \frac{(x - μ ）}{σ} > 0$

k > 0对应于第二类情况，而k < 0对应于III型病例。为k = 0，对应于I型情况，密度为

$y ＝ f （ x | 0 ， μ ， σ ）＝（ \frac{1}{σ} ）经验值（ - 经验值（ - \frac{（ x - μ ）}{σ} ） - \frac{（ x - μ ）}{σ} ）$

背景

与极值分布一样，广义极值分布通常用于模拟一组独立的、同分布的随机值，这些随机值代表测量值或观察值。例如，您可能从一个生产过程中有1000个批次的垫圈。如果您记录了每个批处理中最大的垫圈的大小，则该数据称为块最大值(如果您记录的是最小的，则称为最小值)。你可以用广义极值分布作为块极大值的模型。

广义极值将三个简单分布组合成单一形式，允许包含所有三个简单分布的可能形状的连续范围。您可以使用这些分布中的任何一个来建模特定的块最大值数据集。广义极值分布允许你“让数据决定”哪种分布是合适的。

广义极值分布所涵盖的三种情况通常被称为类型I、II和III。每一种类型对应于不同的底层分布的块极大值的极限分布。尾部以指数形式递减的分布，如正态分布，会导致i型分布，尾部以多项式形式递减的分布，如Student的分布t，导致II型。尾部是有限的分布，如beta，会导致III型分布。

类型I、II和III有时也被称为Gumbel、Frechet和Weibull类型，尽管这个术语可能有点令人困惑。类型I (Gumbel)和类型III (Weibull)的情况实际上对应于通常的Gumbel和Weibull分布的镜像，例如，通过函数计算evcdf和evfit,或wblcdf和wblfit,分别。最后，II型(Frechet)情况等价于从标准威布尔分布取值的倒数。

参数

如果您生成250块1000个随机值从学生t有5个自由度的分布，取它们的最大值，你可以用这些最大值来拟合一个广义的极值分布。

blocksize = 1000;nblocks = 250;rng默认的%的再现性t = trnd (5 blocksize nblocks);x = max (t);% 250列最大值paramEsts = gevfit (x)

paramEsts =1×30.1185 1.4530 5.8929

注意，形状参数估计(第一个元素)是正的，这是您根据Student的块最大值所期望的t分布。

直方图(x, 20分,“FaceColor”,(。8。8 1]);xgrid = linspace (2, 1000);线(xgrid nblocks *.．.gevpdf (xgrid paramEsts (1) paramEsts (2), paramEsts (3)));

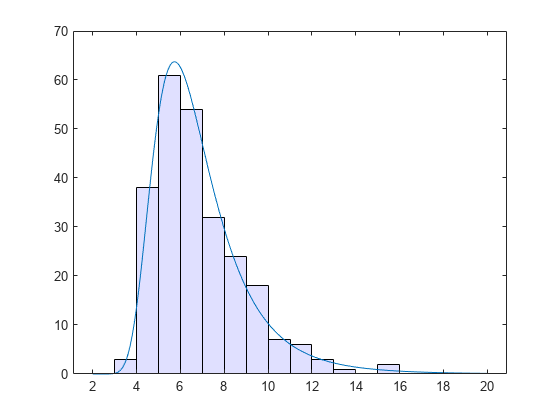
图中包含一个轴对象。坐标轴对象包含两个直方图、直线类型的对象。

例子

计算广义极值分布pdf

打开生活的脚本

为广义极值分布的三种基本形式生成概率密度函数的例子。

x = linspace(3、6,1000);日元= gevpdf (x,闲置,1,0);y2 = gevpdf (x, 0 1 0);y3 = gevpdf (x, 5, 1,0);情节(x, y₁,“- - -”, x, y2,“——”, x, y3,“:”)({传奇'K < 0, III型''K = 0, Type I''K > 0, Type II'}）

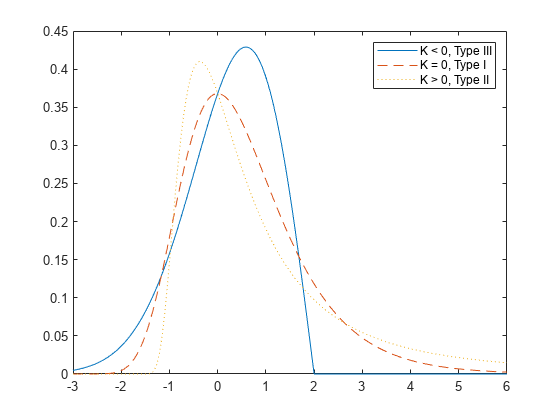
图中包含一个轴对象。轴对象包含3个类型为line的对象。这些对象表示K < 0，类型III, K = 0，类型I, K > 0，类型II。