严格采样小波重建
我们已经学习了如何使用离散小波变换来分析或分解信号和图像。这个过程叫做分解或分析.故事的另一半是如何在不丢失信息的情况下将这些组件组装回原始信号。这个过程叫做重建,或合成.效果综合的数学操作称为逆离散小波变换(得到)。
为了利用小波工具箱™软件合成信号,我们利用小波系数重构信号。

当小波分析涉及到滤波和下采样时,小波重构过程包括upsampling和过滤。上采样是通过在样本之间插入零来延长信号分量的过程。
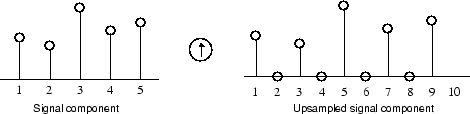
工具箱包括命令,比如得到和waverec,分别对一维信号的分量进行单级或多级重构。这些指令有二维和三维的类似物,idwt2,waverec2,idwt3,waverec3.
重建过滤器
过滤部分重构过程也值得讨论,因为滤波器的选择是实现原始信号完美重构的关键。
在分解阶段对信号分量进行下采样时,会引入一种叫做混叠的失真。事实证明,通过为密切相关(但不相同)的分解和重建阶段仔细选择过滤器,我们可以“抵消”混叠的影响。
关于如何设计这些过滤器的技术讨论在书的347页小波和滤波器组,斯特朗和阮。低通和高通分解滤波器(l和H),以及它们相关的重建过滤器(L '和H”),形成一个所谓的系统正交镜像滤波器:

重建近似和细节
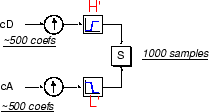
也可以从它们的系数向量重建近似和细节本身。作为一个例子,让我们考虑如何重建一级近似A1从系数向量cA1.
我们传递系数向量cA1通过同样的过程,我们重建了原始信号。但是,我们并没有将其与第一级细节相结合cD1,我们输入一个零向量来代替细节系数向量:

这个过程会产生一个重构的结果近似A1,它与原始信号的长度相同年代这是它的真实近似值。
类似地,我们可以重建第一级的细节D1,使用类似的过程:

重建的细节和近似是原始信号的真实成分。事实上,我们发现当我们把它们结合起来
一个1+D1=年代.
注意系数向量cA1和cD1-因为它们是通过下采样产生的,而且只有原始信号长度的一半-不能直接合并来再现信号。在将这些近似和细节进行组合之前,有必要对它们进行重构。
将这种技术扩展到多电平分析的分量,我们发现类似的关系适用于所有重构信号的分量。也就是说,有几种方法可以重新组装原始信号:

共轭镜滤波器的小波
一节中重建过滤器,我们谈到了选择正确过滤器的重要性。事实上,滤波器的选择不仅决定了完美重构是否可能,还决定了我们用来进行分析的小波的形状。
要构造一个实用的小波,你很少从画一个波形开始。相反,设计合适的通常更有意义正交镜面滤波器,然后用它们来创造波形。让我们通过一个例子来看看这是如何做到的。
考虑低通重构滤波器(L ')db2小波。
滤波系数可由dbaux函数。通过反转缩放滤波器向量的顺序,并将每个偶数元素(从1索引)乘以(-1),就可以得到高通滤波器。
对输出信号进行二次上采样并与尺度滤波器进行卷积,得到Daubechies的极值相位小波。
L = dbaux (2);H = wrev (L)。*[1 -1 1 -1];胡= dyadup (H, 0);胡= conv (HU L);情节(胡);标题(第一个迭代的);H1 = conv (dyadup (HU 0), L);H1, H2 = conv (dyadup (0), L);H3 = conv (dyadup (H2, 0), L);H4 = conv (dyadup (H3, 0), L);图;为k = 1:4次要情节(2 2 k);eval ([“情节(H”num2str (k)“)”]);轴紧;结束
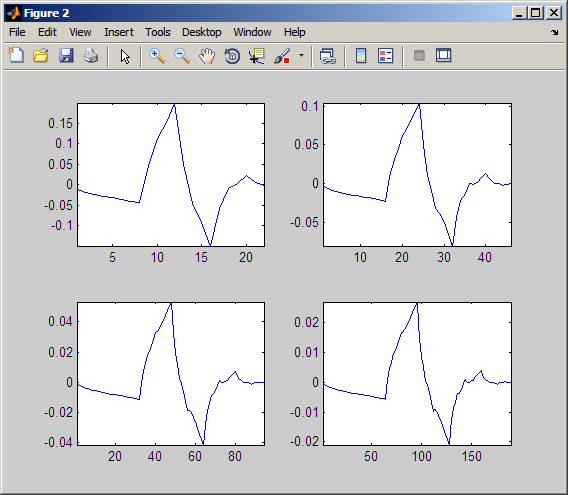
曲线开始变得越来越像db2小波。这意味着小波的形状完全由重构滤波器的系数决定。
这种关系有着深远的影响。这意味着你不能选择任意形状,称之为小波,然后进行分析。至少,如果你想准确地重建原始信号,你不能选择任意的小波波形。你必须选择一个由正交镜分解滤波器决定的形状。
尺度函数
我们已经看到了小波和正交镜滤波器的相互关系。小波函数ψ是由高通滤波器确定的,它也产生小波分解的细节。
有一个附加的函数与一些,但不是所有的小波相关。这就是所谓的尺度函数ϕ。尺度函数与小波函数非常相似。它是由low-pass决定的正交镜滤波器,因而与小波分解的近似有关。
重复上采样和卷积高通滤波器产生近似小波函数的形状,重复上采样和卷积低通滤波器产生近似尺度函数的形状。

