反常端口传递问题

发布的罗兰美国舒尔，2017年2月14日

12次观看(过去30天)|0喜欢|0评论

今天的特邀博主是乔斯马丁他来自MathWorks的并行计算组。虽然通常专注于在MATLAB中使并行计算既简单又快速，但偶尔他喜欢使用MATLAB来探索其他问题空间。在这里，他写了一个有趣的随机游走过程，他遇到了这个过程，使他能够在MATLAB中探索模拟和分析方法，并使用这些方法来帮助指导其他方法。

内容

简介

π的一天即将到来，你被邀请与一位古怪但有数学头脑的主人共进晚餐。她提供了很多有趣的美食现在你有了终于来到了在奶酪的课程；当然，波尔图葡萄酒配上一轮美妙的斯蒂尔顿葡萄酒。然而，他不顾常规(向左传球)，她让客人们随机选择一个方向，从哪个方向喝葡萄酒。你绕着圆桌走了一圈，对这个奇怪的事件转折感到某种程度的惊愕。你应该担心吗?你在谈判桌上的位置如何影响你成为最后一个接受这个例外的人的可能性丰63？对于那些立刻担心葡萄酒可能会用完的迂迂的少数人，我可以断言，她是一个非常好客的主人，并向她的客人保证，滗水器将继续从端口管她最近收购了．有人可能会提出的另一个问题是:平均会消耗多少端口(假设每个客人在每次传递时都使用固定数量的端口)?这个问题可以用a来建模随机漫步，本质上类似于一个被充分研究过的案例赌徒的毁灭．这里的主要区别在于，你需要拜访餐桌周围的所有位置，而不是简单地到达走道的一端或另一端。为了探索这个看似简单的问题，我将首先使用一种有助于指导分析方法的模拟方法(在将来)帖子)．为了做到这一点，我将使用统计学和符号数学工具。

模拟方法

有很多分析方法可以解决这个问题(我将在本文中引用其中的一些方法文件和证明都可以在File Exchange上找到)，但这里我想重点谈谈蒙特卡罗模拟的方法。为了举例说明这种方法，我们将运行nSims独立模拟之间传递醒酒器N人(总是从0人开始)，有一个概率p左边的传球(和1 - p右通过)。

nSims = 100;N = 11;P = 0.5;

模拟米穿过港口的通行证nSims模拟我们做一个矩阵singleMove仅包含值1和-1，表示使用统一随机数向左或向右传递端口。

M = 25;singleMove = 2*(rand(nSims, M) >= p) - 1;% 6次模拟的前6个通过方向disp (singleMove (1:6, 1:6));

1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

通过知道每一次通过的方向，我们可以通过计算每一次通过的方向的累积和来计算端口的位置与它的起点相比。为了使其成为绝对位置，我们将起始位置(在本例中为0)加上。因为我们需要考虑到滗水器在桌子周围的移动，所以我们将使用模数N将课程折叠回可用位置的算术。

Start = 0;location = mod(cumsum(singleMove, 2) + start, N);% 6次模拟的前6个位置disp(位置(1:6,1:6))

10 9 10 0 10 10 9 10 0 10 0 10 0 10 0 10 10 9 10 0 1 2 10 10 0 10 0 10 0 10 9 8 7 8 9

我们现在有一个矩阵位置其中包含了20次传递的100次模拟。是否所有的模拟都达到了桌边的所有位置?在函数中portPassingSimulation我们将遍历每一遍，看看哪些模拟在该遍历中完成了，但在这里，我们将简单地计算是否有任何模拟完成了。为了完整，一个模拟需要访问所有0: n - 1可能的位置。问这个问题的一个简单方法是查看该模拟是否包含N独特的元素。如果是，它一定去过所有可能的地点。

finished = false(nSims, 1);为ii = 1:nSims finished(ii) = numel(唯一的(位置(ii，:))) == N;结束nFinished = sum(已完成)

nFinished = 10

对于那些尚未完成的模拟，我们知道它们的当前位置(由位置(:,结束))，因此可以模拟另一个块nSims x M通过，继续前进，直到所有模拟都达到目标。完整的模拟代码(portPassingSimulation可用在这里)返回最后一个位置、到达该位置的通过次数、到达最后一个位置的方向以及在每次模拟过程中对表周围每个位置的访问次数。该代码紧密地基于此策略，并带有稍微不同的停止检测策略。

[last, nPasses] = portPassingSimulation(nSims, N, p);results = table(last, nPasses);disp(结果(1:10,:))

last nPasses ____ _______ 7 215 7 129 8 127 8 127 3 124 10 108 4 102 8 102 5 101 3 98

正在调查港口的最终位置

我们给自己设置的第一个问题是，我们在桌子周围的位置是否会影响我们成为最后一个接收端口的人的概率。为了看这个，让我们运行一个相当大的数字(10^5美元)的模拟，看看有多少最终在每个n - 1可能的结束位置。

last = portPassingSimulation(1e5, N, p);嘘(最后1:n - 1);网格在标题“10^5次模拟11个人围坐在桌子旁”包含“最后一个接收港口的人”ylabel“那个人最后的次数”

从这个柱状图中我们感到极大的宽慰!这表明，无论我们坐在餐桌的哪个位置，我们作为最后一个接受端口的人的次数都是和其他人一样的。我们坐在餐桌的哪个位置都不重要!这个结果似乎与直觉相反;当然，你距离起跑点的距离应该会影响你最后一名的可能性吧?首先，让我们看看对于不同大小的表，结果是否相同。我们可以在更多人的情况下运行模拟器进行检验。

last = portPassingSimulation(1e5, 41, p);嘘(最后,1:马克斯(去年));网格在标题“10^5次模拟41个人围坐在桌子旁”包含“最后一个接收港口的人”ylabel“那个人最后的次数”

有一种直观的方式来描述最后一个的概率与你坐在桌子上的位置无关。最后，醒酒器必须到达你的左边或右边，然后穿过整个桌子，没有经过你。不管你坐在桌子的哪个位置，那组动作的概率都是一样的——因此你最后一个的概率也是一样的。

通过时最后一个位置的分析概率是无偏的

我们可以分析地表明，最后一个的可能性与你在桌子上的位置无关。我们需要引用一个结果赌徒破产分析．设$pSAB$为滗水器从位置S开始，在到达位置b之前到达位置A的概率。此概率等同于从初始股份(sb)，并在赌注输掉或赢钱(a - b)．$ $ pSAB = \压裂{sb} {A - B} \ mbox {B} < S < \ mbox{或}< S < B美元我们可以使用美元符号数学工具箱不需要自己做代数运算就能处理方程(对我来说，这样就不太可能出现转录错误)。在这种情况下某个位置k是最后一个的概率是

从位置0开始，到位置L(编号k-1)不到达位置R(编号k+1)，同时从位置L到位置R不到位置k
从位置0开始，到位置R不到达位置L，然后从位置R到位置L不到位置k

根据$pSAB$可以写成:

信谊pSAB (S, A, B)kNpSAB(S,A,B) = (S-B)/(A-B);L = k-1;R = k+1-N;plasunbiased = simplify(pSAB(0,L,R)*pSAB(L,R,k) + pSAB(0,R,L)*pSAB(R,L,k- n))

pLastUnbiased = 1/(N - 1)

请注意，为了确保$Ak +其它为什么在最后一项中k - n而不仅仅是k．这保证了$k>L \ge 0 \ge R > k- n $。结果体独立于k并且显示了相同的可能性，与模拟一致。

如果向左或向右通过的概率有偏差会发生什么?

上面的模拟假设任何晚餐客人从左边或右边经过的概率是相等的。如果一个方向有轻微的偏差呢?这会对你在港口的享受产生明显的影响吗?让我们模拟一种情况，其中通过左边的概率是0.54(而不是0.5)。

N = 17;P = 0.54;k = 1:N-1;nSims = 1e5;last = portPassingSimulation(nSims, N, p);嘘(最后,k);网格在标题“模拟桌子周围17个人的偏传”包含“最后一个接收港口的人”ylabel“那个人最后的次数”

从这张直方图中可以清楚地看出，即使概率中的一个小偏差也会极大地影响我们最后一个的可能性。我们可以通过研究来决定我们需要参加多少次晚宴，然后才能合理地推断出酒瓶有偏差，但那是另一个故事了!

这个有偏差的模拟与理论一致吗?

使用与上面的分析方法非常相似的方法(参见下一篇文章(不是马上直播)对于推导)，我们可以证明最后一个的偏概率是$$P_{last}=\frac{r^N(1-r)}{r^k(r-r^N)} \mbox{其中}r=\frac{1-p}{p} \mbox{和}p\ne \frac{1}{2}$$在模拟的顶部绘图显示非常好的一致性。

R = (1-p)/p;pLastBiased = r^N*(1-r)./(r.^k*(r-r^N));持有在情节(k, pLastBiased * nSims,“罗”，“MarkerSize”8“线宽”2);持有从

谁喝得最多?

现在我们知道每个客人都是最后一个收到葡萄酒的人，我们可以看看醒酒器传递给每个客人到最后一个人的总次数。这对在座的每个人来说都一样吗?有偏差的通过概率会改变它通过每个人的次数吗?

nSims = 3e4;N = 25;[~， ~， ~， visitsUnbiased] = portPassingSimulation(nSims, N, 0.5);[~， ~， ~， visitsBiasedL] = portPassingSimulation(nSims, N, 0.53);[~， ~， ~， visitsBiasedR] = portPassingSimulation(nSims, N, 0.47);图保存在阴谋(1:n - 1, visitsUnbiased / nSims,“啊——”) plot(1:N-1, visitsBiasedL/nSims，“啊——”) plot(1:N-1, visitsBiasedR/nSims，“啊——”)举行从网格在传奇(“无偏传递”，“偏见left-pass”，“有偏了”，“位置”，“N”)标题“每一位客人的酒瓶拜访”包含“餐桌位置”ylabel“醒酒器经过位置的次数”

从图中我们可以看到，靠近酒瓶初始位置(位置1)的客人接受和传递葡萄酒的频率(对于这个尺寸的桌子来说)略低于对面客人的两倍，并且随着传递变得有偏差，桌子的一边比另一边更有可能接收更多的葡萄酒。我们还可以看到，无偏情况下平均传递次数最多，我们可以通过考虑在p==1(或p==0)的情况下，每个位置接收端口的次数只有一次来猜测!

客人的数量会影响每人喝多少酒吗?

上面的图是针对单个表大小(N == 25)．如果我们有不同的表大小会发生什么?港口对每个地点的访问次数之间是否存在根本关系?显然，我们需要一种方法来比较不同大小的表和不同数量的模拟的访问。我们将绘制一个规范化位置的所有结果[1]哪个映射到整数位置1: n - 1．此外，我们需要以某种方式使访问正常化。要做到这一点，我们将每个位置的访问数量作为该表预期访问数量的比例(如果每个位置都被平等地传递)。要做到这一点，我们将每个地点的访问次数除以总访问次数，再乘以餐桌上的人数。对于每个位置都有同等人数的表，这将在每个位置产生值1，表明对该位置的预期访问数是1乘以平均分布的数。

图保存在网格在tableszes = [5 10 14 15 20 30 35];为kk = tableszes[~， ~， ~，访问量]= portPassingSimulation(1e4, kk+ 1,0.5);Plot (linspace(- 1,1, kk)， kk*访问量/sum(访问量)，“。”）结束持有从传奇(string (tableSizes),“位置”，“N”)标题对于给定的表大小，保持端口的相对可能性包含“规范化表大小”ylabel“持酒瓶的相对可能性”

这里看起来是一个二次关系式;我们鼓励感兴趣的读者对此进行探索，并在表大小变化时为关系生成函数形式，并查看随着表大小的增加，平均访问次数如何变化。

左舷的管子会用完吗?

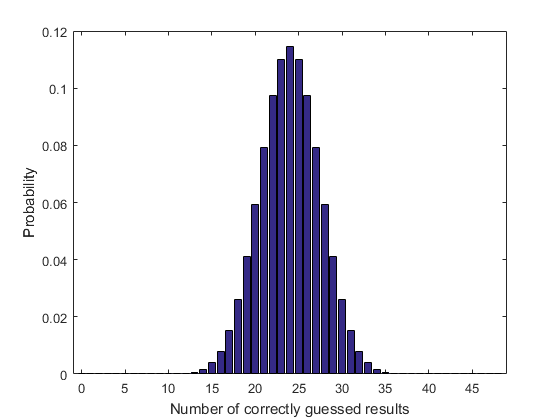
假设每位客人带了2 fl.oz。每次醒酒器经过他们的时候，都要喝一杯波特酒。然后，我们可以通过跟踪每个模拟完成所需的迭代次数来计算给定模拟中消耗了多少端口。的第二个输出portPassingSimulation返回到达最终位置所需的通道数。在所有模拟中，这将为我们提供所需完成的通道的分布函数。

nSims = 1e5;N = 31;P = 0.5;binW = 50;[~， nPasses] = portPassingSimulation(nSims, N, p);嘘(nPasses 30: binW:马克斯(nPasses));持有在网格在

如果您感兴趣，有必要看看使用的这个发行版分布更健康从统计和机器学习工具箱．它似乎很适合使用对数正态分布或Birnbaum-Saunders分布。我们可以用fitdist函数并在直方图上绘制预期分布

pd = fitdist(npass，对数正态的) x = linspace(1, max(nPasses)， 200);plot(x, nSims*binW*pdf(pd, x)，“r”）;持有从标题“总通行证的分布”包含“所有晚宴客人的通行证数量”传奇(“模拟PDF”，对数正态分布的预期PDF）

对数正态分布mu = 5.98543 [5.98189, 5.98897] sigma = 0.570894 [0.568403, 0.573407]

我们可以用概率图来看看对数正态分布对数据的拟合程度。你可以看到尾部的分布是不正确的。

probplot (对数正态的， nPasses)网格在

LogNormal和Birnbaum-Sanders都高估了平均值附近的传递次数，低估了平均值的1.5倍左右，所以尽管它们很好地拟合了分布，但实际上它们并没有正确地建模。拟合分布和实际分布的平均值如下所示。

fittedMean = pd。mean actualMean = mean(nPasses)

fittedMean = 467.96 actualMean = 465.29

为了解释这种无法拟合模拟数据的情况，我们将在接下来的分析中使用经验平均值。如果我们更确定我们理解了期望分布，我们将使用拟合分布。

预测端口消耗量

接下来，让我们来研究一下在桌子上的人数和端口在桌子上经过的预期次数之间是否存在简单的关系。我们可以做一些不同的模拟，看看平均数和人数之间的关系。让我们在餐桌尺寸上这样做2:30无偏的通过概率。为了加快计算速度，我们使用a并行循环从并行计算工具箱，因为每个模拟都是相互独立的。默认情况下，如果一个并行池尚未打开，这将自动打开。

P = 0.5;tableSize = 2:30;tToFinish = 0 (size(tableSize));parforii = 1:numel(tableSize) [~， nPasses] = portPassingSimulation(1e5, tableSize(ii)， p);tToFinish(ii) = mean(nPasses);结束情节(tableSize tToFinish,“o”)标题“平均完成次数vs.客人数量”包含“饭桌上的人数”ylabel“到达所有人的平均通道数”网格在

看起来这些量之间有很强的多项式关系。4次和2次的多项式拟合是什么样的?

f2 = polyfit(tableSize, tToFinish, 2)

F4 = 1.8679e-05 -0.0011103 0.52081 -0.63573 0.24387 f2 = 0.49955 -0.49157 -0.015421

注意三阶和四阶参数f4基本上是零?这表明，仅使用二阶多项式就能很好地拟合数据。

持有在x = linspace(min(tableSize)， max(tableSize)， 100);Plot (x, polyval(f2, x)，“r”）;持有从传奇(“分布的测量平均值”，“二次安装”，“位置”，“西北”）

解析猜想

我还注意到的值是多么接近f2是[0.5 -0.5 0]．这似乎好得令人难以置信!如果您运行更多的模拟(例如，从表大小2:100)，每个表大小的模拟次数越多，多项式拟合的平均值就越接近这个值集。我的猜想是，对于这么大的一张桌子N我们可以通过运行一些不同的模拟来对一些表大小尝试这个猜想，去掉该表大小的期望通过数，并查看残差，看看它们的平均值是否为零。

残差=零(60,1);parforIi = 1:60使用表大小9:4:29N = 9 + 4*mod(ii, 6);[~， nPasses] = portPassingSimulation(1e5, N, 0.5);eMeanPasses = polyval([0.5 -0.5 0]， N);残差(ii) = mean(nPasses) - eMeanPasses;结束残差是否来自均值为零的正态分布?我们可以%使用t检验来看待这一点[H1, pVal1, CI, stats] = ttest(残差)

H1 = 0 pVal1 = 0.32436 CI = -0.18322 0.061617 stats = struct with fields: tstat: -0.99384 df: 59 sd: 0.47389

输出(H = = 0)从t检验表明，我们不能拒绝零假设-数据可以从零均值的正态分布中提取，并且仅具有概率pVal我们会期望一个不太像正态分布的随机分布吗。观察一些这样的结果，我们可以看到分布的尾部实际上并不是正态的，所以我们可以使用“t-location scale”概率图来看看残差是如何被分布拟合的。如果吻合得很好，那么所有的点都应该在直线上。

Pd = fitdist(残差，“tLocationScale”）;Probplot (pd，残差)网格在标题“t位置尺度分布的概率图”

最后，我们可以使用卡方拟合优度检验，测试数据来自该拟合分布的可能性，但均值为零

pd。Mu = 0;[H2, pVal2] = chi2gof(残差，“提供”, pd)

H2 = 0 pVal2 = 0.57262

这似乎符合得相当好，表明我们的猜想似乎符合数据。关于这个猜想的分析证明，请参阅我的下一篇博客文章。因此，我们现在终于可以回答关于端口管道耗尽的问题，因为我们可以预测给定表大小的平均通过数。

1008品脱，2 fl.oz。玻璃%和20 fl.oz。英制品脱pintsInPipeOfPort = 1008;maxPasses = pintsInPipeOfPort*20/2;N = sym(“N”）;假设(N > 0)使用符号数学工具箱来解决k的方程double(solve(N*(N-1)/2 == maxPasses, N))

Ans = 142.49

这告诉我们，142张桌子的大小不到一半的晚餐将用完!

港口消耗的数量与最终位置有什么关系?

我们可以研究的问题的最后一个方面是，总体路径长度(以及因此消耗的端口数量)如何随着最后到达的位置而变化。考虑到距离起点较近的位置需要经过的路径，而不是距离起点较远的位置，我们可能会直觉地认为越近的位置可能越短。让我们看看情况是否如此，以及路径如何随着传递变得有偏差而变化。首先，我们需要运行模拟(对一个大小为17的表进行无偏置)。

N = 17;P = 0.5;[last, nPasses] = portPassingSimulation(5e5, N, p);

接下来，查看通过次数的平均值，但将这些平均值按可能的最后位置分组。有一个非常简单的方法来做到这一点varfun表的方法，并按变量分组最后的．

G = varfun(@mean, table(last, nPasses)，“GroupingVariable”，“最后一次”）

G = last GroupCount mean_nPasses ____ __________ ____________ 1 31392 100.71 2 31392 114.98 3 31256 127.18 4 31205 137.1 5 31209 144.15 6 31254 151.21 7 31255 155.31 8 31429 156.65 9 30950 156.79 10 31405 155.29 11 31182 150.78 12 31333 144.77 13 31276 136.87 14 31015 127.2 15 31313 115.35 16 31134 100.88

绘制平均路径图，我们可以看到，距离零点最近的位置路径最短，距离零点最远的位置路径最长。

情节(G。最后的，G.mean_nPasses,“o”)标题“给出最后一个位置的预期传球次数”包含'最后接收端口的位置'ylabel“预期通过次数”网格在

最后，看看如果情况变得有偏差会发生什么，我们可能会期望具有最长期望路径的位置会转移到一边(即更接近开始位置)。事实上，考虑p趋近于1的极限，我们应该期望到位置N-1的路径长度简单地变成N(因为滗酒器将从k到k+1的概率接近于1)。N-2的路径长度可能非常接近于N-1的路径长度，在表的某个地方向右偏移(接近于零概率)。因此，对于p > 0.5，我们期望路径长度的峰值向位置0移动，并且k = N-1的期望路径长度比k = 1的短。

N = 17;P = 0.57;[last, nPasses] = portPassingSimulation(5e5, N, p);G = varfun(@mean, table(last, nPasses)，“GroupingVariable”，“最后一次”）;情节(G。最后的，G.mean_nPasses,“o”)标题'给定最后位置的预期传球(偏向传球)'包含'最后接收端口的位置'ylabel“预期通过次数”网格在

最后

在探索这个问题的过程中，我最喜欢的一点是，它的陈述非常简单，但随着我的进一步研究，我发现它有多么复杂。一开始，我只是简单地问一个人最后出现的可能性有多大，但我最终学会了如何解决相当复杂的递归关系，并探索了我不知道的随机游走的方面。此外，我还发现模拟的实验性质，结合解析的严谨性来解决随机游走过程的数学问题具有启发性。能够将MATLAB的这两个不同方面结合在一起，并让仿真结果帮助指导分析发现，这并不常见(至少对我来说)。几周后我将发布另一篇关于我如何使用的文章符号数学工具箱分析推导出这些期望路径长度，并将结果与模拟结果进行比较。与此同时，也许你可以进一步分析?到目前为止我忽略的一个方向是推导路径长度分布的期望形式。或者也许你有一个相关的随机游走过程，可能会屈服于类似的分析?让我知道在这里．

发布与MATLAB®R2016b