内容

介绍

希望你回忆起最近的帖子我们使用过的地方Monte-Carlo技术模拟一个无限的港口滗水器，通过桌子N人们（始终从位0开始），概率移动p到左边问在右边，只有在桌子上的每个人都收到了一些港口时才停止。这些模拟似乎表明，可以展示预期的路径长度的简单分析解决方案，我将向您展示我设法证明的内容。金宝搏官方网站

在最后一篇文章中，我们决定我们想找到的功能是

赌徒的毁灭

感谢我的同事Rick Amos，我们有了一个思考分析解决方案的起点。他指出，我们的端口通过问题与随机游走过程非常相似赌徒的毁灭，赌徒从一些股份开始（k)，并以概率赢得另一单位的赌注p（或丢失概率1-P.）.游戏继续，直到赌徒输掉所有的钱，或者总共输掉所有的钱N．主要区别在于，在赌徒的废墟中有两个不同的最终条件（获胜N或失去0）.

为了解决端口传递问题，我需要引用《赌徒的毁灭》中的两个结果。你可以在。中找到这些结果的推导相关文件文件交换(请参阅文件BiasedGamblersRuin和UnbiasedGamblersRuin）.第一个结果使我们能够回答这个问题:“给定我们目前在位置S，在到达位置B之前到达位置A的概率是多少?”在《赌徒的毁灭》中，这与开始时的赌注$k=S-B$和结束时$N=A-B$相同。为了简化一些方程，我将使用$q=1-p$，注意，我们假设$A

$ $ pSAB左= \ \ lbrace \开始{数组}{cc} \压裂{k} {N} & p = = \压裂{1}{2}\ \ \压裂{第一轮^ k}{第一轮^ N} & p \ ne \ mbox{和}r = \压裂{q} {p} \结束数组{}\ $ $

同样，我们还需要回答：“在抵达位置之前到达位置A的位置（在S）中的预期传递数量是多少？”。

$$ esab = \ left \ lbace \ begin {array} {cc} {cc} \ frac {n ^ 2-k ^ 2} {3}＆p = q = \ frac {1} {2} \\\ frac {1+r} {1-r}（n（\ frac {2} {1-r ^ n} -1）-k（\ frac {2} {{1-r} ^ k} -1））和p \ neQ \结束{array} \右。$$

注意每个结果如何对偏见和非偏见的情况有不同的表达式？下面我们将通过偏见的案例（具有更复杂的）。完全相同的代码可以使用非偏见的情况和获得的正确结果 - 如果您有兴趣只是更改Ptouse.下面回到0.5和执行。

Syms.Psab（s，a，b）esab（s，a，b）p问kNptouse = 0.55;假设（p == ptouse）;％在S，A和B方面定义K和N的功能。k (S, A, B) = sb;N (S, A, B) = A - B;如果ptuse == 0.5 pSAB(S,A,B) = k/N;eSAB(S,A,B) = (N²- k²)/3;其他的在有偏的情况下，方程中我们将使用r而不是pSyms.r假设(r ~ = 1);pSAB (S, A, B) =(第一轮^ k) /(第一轮^ N);伊萨(S, A, B) = (1 + r) /(第一轮)* (N *(2 /(第一轮^ N) 1) - k *(2 /(第一轮^ k) 1));结束

允许我们谈谈位置的一般情况k是最后一个接收围绕大小的港口的港口N我们将使用职位l指某人右边的位置k和R左边的一个k（注意使用Modulo算术以确保$ K-N

Syms.lRNkl = k-1;r = k + 1-n;

计算位置的概率k是最后一次

对于位置k要成为最后一个，我们要么需要端口从起始位置0移动到L，然后到R，要么从0移动到R，然后到L，这个概率是由

$ $ p_k = pSAB (0 L R) * pSAB (L R k) + pSAB (0, R, L) * pSAB (R, L, k) $ $

p0L = pSAB(0, L, R);p0R = pSAB(0, R, L);pLR = pSAB(L, R, k);pRL = pSAB(R, L, k-N);p0LR = p0L * pLR;p0RL = p0R *光杆载荷;pk =简化(p0LR + p0RL)

PK =  - （r ^ n *（r  -  1））/（r ^ k *（r  -  r ^ n））

在之前的博文中，我们证明了在无偏情况下，这个结果与位置无关k，但在有偏差的情况下，桌边的位置会影响最后的概率。让我们看看一些模拟的残差来检查这是否正确portpassingsimulation.代码是可用的在这里）.

p = pToUse;N = 17;k = 1: n - 1;nSims = 1 e5;残差=南(10、n - 1);subs(pk， {)“r”“N”“k”}，{（1-p）/ p，n，k}））;％模拟10次通过17桌子parforii = 1:10 last = portPassingSimulation(nSims, N, p);%将模拟分成k (1:N-1)个bins，并按模拟的数量进行归一化lastProb = hist(last, k)/nSims;residuals(ii，:) = lastprobb - expected;结束％是通常分布的残差？probplot (“正常”，残差（:)）网格在

我们可以看到仿真的残差大致分布（某些尾部点不正常），但没有任何偏差来自预期结果（因为残差的平均值接近于零）。

VILMR =均值（残差（:)）

VILMR = 7.5894E-20

我们需要考虑哪些路由来计算预期的路径长度?

要计算预期的路径长度，我们将不得不考虑最终以位置结束的所有可能的路径k，计算出每条路径发生的概率，然后乘以该路径的期望长度。幸运的是，虽然存在无限多的可能路径，但我们可以将问题分解成与《赌徒的毁灭》直接相关的2个路径。这些是L路线和R路线

替代路线r（基本上是路线l的逆）是

路径每一部分的期望长度是

Syms.kNe0l = esab（0，l，r）;e0r = esab（0，r，l）;Elr = esab（l，r，k）;ERL = esab（r，l，k-n）;ERK = esab（r，k-n，k）;麋鹿= esab（l，k，k-n）;erlk = esab（r，k，k-n）;Elrk = esab（l，k-n，k）;

值得注意的是，预期路径长度伊萨交换变量是对称的吗p和问．我们可以在上面的等式中看到它ELR = =话务量，ERk = =麋鹿和Erlk == Elrk.

简化(ELR == ERL)简化(ERk == ELk)

ans = TRUE ans = TRUE

将路线L和路线R的部分组合在一起的选择，我们需要包括L和第3部分和R的第3部分和第3部分和第4部分的概率。这些只是赌徒废墟中这些路径的概率。

PRK = PSAB（R，K-N，K）;PLK = PSAB（L，K，K-N）;prlk = psab（r，k，k-n）;PLRK = PSAB（L，K-N，K）;

所以最后，我们可以将这些零件结合起来的两条路线。埃尔是L和的预期路径吗呃路由R的预期路径长度。

EL = E0L + ELR + pRk。* ERk + pRLk。* ERLk;ER = E0R + ERL + pLk。*麋鹿+ pLRk。* ELRk

呃= ((1 / r - 1) * (r + 1) * (2 / (1 / r - 1) - N * (2 / (1 / r ^ N - 1) + 1) + 1) / ((r - 1) * (1 / r ^ N - 1)) ((((2 / (r ^ 2 - N) (- 1) + 1) * (N - 2) (2 / (r ^ (1 - k) - 1) + 1) * (k - 1)) * (r + 1)) / (r - 1) - ((r + 1) * (2 / (r - 1) - (N - 1) * (2 / (r ^ (N - 1) - 1) + 1) + 1) / (r - 1) - (((N - 1) * (2 / (r ^ (N - 1) - 1) + 1) - N * (2 / (r ^ N - 1) + 1) * (r + 1) * (r ^ (N - 1) - 1)) / ((r ^ N - 1) * (r - 1))

我只打印了一个结果，只是表明目前这看起来很复杂！希望这将使某种方式更简单！

端口选择路径L或R的概率

为了能够计算整个预期路径，我们还需要知道端口采用路径L或R的概率，因为

$E_k = p_L E_L + p_R E_R$

幸运的是，我们已经有了通过分析完成位置概率来计算这些概率的组件。路径L的概率等于从0到L到R的概率除以k最后的概率。同理，对于路径R。

PL =简化（P0L * PLR / PK）PR =简化（P0R * PRL / PK）

pL = (^ N - r ^ (k + 1) / (r ^ N - r ^ 2)公关= - (r * (r - r ^ k)) / (r ^ N - r ^ 2)

计算预期的路径长度k是最后一次

有了这些结果，我们可以通过将两个可能的路径长度相加，乘以它们的概率来计算预期长度。

埃克=简化(pL。*EL + pR.*ER, 400)

ek =（2 *（2 * n  -  k  -  3 * r ^ n + n * r ^ n  -  n * r ^ k + k * r ^ n + 1））/（（r ^ n  -  1）*（r- 1)) - (k - 2*N + N*r^N + N*r^k - k*r^N)/(r^N - 1) - 4/(r - 1)^2 - (2*r^N*(r^N + 1)*(N - 1))/((r - r^N)*(r^N - 1))

这与模拟相符吗?

我们可以看看效果如何埃克通过运行模拟并计算每个精加工位置的平均通行证的平均数量来同意模拟数据。正如我们在以前的博客文章中看到的那样，通过使用，这是一种简单的方式来看看每个最后一个位置的平均传球数量是varfun.对于表，具有分组变量。

p = pToUse;N = 17;k = 1: n - 1;[最后，npass] = portpassingsimulation（1e6，n，p）;t = varfun（@mean，表（最后，npass），......'分组不可行'，“最后一次”）

T =最后GroupCount mean_nPass ____ __________ __________ 1 9291 95.262 2 11379 111.75 3 13888 123.74 4 17016 130.06 5 20845 135.69 6 25541 136.47 7 31030 136.05 8 38271 133.8 9 46659 130.33 10 56701 125.85 11 69383 119.94 12 84602 112.84 13 1.04E + 05 106.3914 1.2629E + 05 98.765 15 1.5536E + 05 90.384 16 1.8975E + 05 82.086

策划这些反对分析结果给出

cMean = double(subs(Ek， {))“r”“N”“k”}， {(1-p)/p N k}));情节(t。最后,t.mean_nPass,“罗”）;持有在情节(k, cMean,“。”） 网格在持有离开标题'模拟VS预期的通行证数量包含'仓位港口最后在桌子上'ylabel.“到达最后位置的平均传球次数”传奇（的仿真结果，'预期结果'）

最后，平均值和预期的差异几乎是零

意思是(cMean(:)——t.mean_nPass (:))

ans = -0.041108

残差的平均值接近于零，表明模拟数据与公式一致。

对于大小为N的表，平均需要通过多少次?

已经推导出当最后一个位置是k，我们现在终于可以计算size表的预期路径长度了N因为我们可以简单地将每个可能的k位置的预期路径总和，所以位置k是最后一个概率的概率。

$ _{k=1}^{N-1} p_k E_k$$

Syms.kNren =简化（Symsum（PK * EK，K，1，N-1），1000）

en =（n ^ 2 *（r + 1））/（（r ^ n  -  1）*（r  -  1）） - （（r + 1）*（n + r  -  n * r））/（r-  1）^ 2 +（r *（n  -  1）^ 2 *（r + 1））/（（r  -  r ^ n）*（r  -  1））

谢天谢地，这看起来比之前的一些结果简单多了。

检查已知的分析解决方案

在继续之前，我们可以通过几种方式检查这一结果。首先，让我们专门检查一下n == 3.我们已经知道分析解决方案的情况（见symbolicaalysisfor3people.mlx.）

$ $ E_3 = \压裂{3}{问^ 2 - q + 1} 1 $ $

以n的值代替n和r的等式

E3 = simplify(subs(EN， {N, r}， {3 q/(1-q)})， 400)

E3 = 3 /（q ^ 2  -  q + 1） -  1

或者，我们可以针对某些模拟来检查结果，用于不同的n

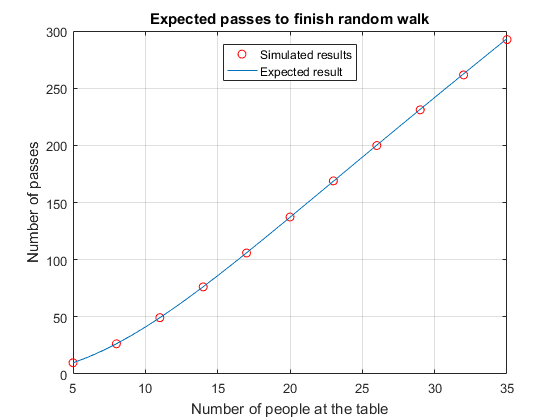
p = pToUse;tableSize = 5:3:37;sim =南(大小(tableSize));parforII = 1：NUMER（Tablingize）n = tablyize（ii）;[〜，npass] = portpassingsimulation（1e5，n，p）;SIM（II）=平均值（纳通）;结束情节(tableSize sim卡,“罗”） 网格在持有在n = min（tablesize）：max（tablesize）;预期=双（潜艇（zh，{“r”“N”}, {(1 - p) / p N}));情节(N,预期);持有离开标题“完成随机行走的预期通过”包含“餐桌上的人数”ylabel.“程数”传奇（的仿真结果，'预期结果'，'地点'，“N”）

把有偏和无偏的结果全部写出来，我们得到

$$ e_n = \ left \ lbace \ begin {array} {cc} \ frac {n（n-1）} {2}＆p = q = \ frac {1} {2} \\\ frac {r + 1} {r-1}（\ frac {n ^ 2} {r ^ n -1} - \ frac {{{（n-1）} ^ 2} {r ^ {n-1} -1} + \ frac {Nr-N-r}{r-1})& p\ne q\end{array}\right.$$

用这种方式写入，它是非常复杂的，但有一个对称性。n在n，在n-1和另一个术语中相同的术语。一贯的全部明显更简单呃我将进一步打印出页面。并且我们已经为我们想要调查的所有值产生了分析解决方案 - 也许现在是时候通过港口金宝搏官方网站了！

最后

通过将所有的预期路径与概率结合在一起而得到的相当复杂的代数表达式的操作，我认为如果用手来做的话，将会非常困难。不过我想你会同意用符号数学工具箱使它成为易行的。我对解决复发关系的能力印象深刻（参见证明初始定义的相关文件诗篇和伊萨）.

从文章中，它可能看起来像我自己完成了所有的工作，所以我要感谢两者瑞克阿摩司(MathWorks)和巴纳比·马丁(杜伦大学)，感谢他在许多细节上的帮助。

看到这些相关的博客帖子，你现在可以使用模拟攻击哪些问题来指导您的数学方法？你能看到机会将统计数据和象征性操纵在一起吗？让我知道在这里．

获取matlab代码

发布与MATLAB®R2016b