四元数是复数的一般化，在计算机图形学和许多其他领域都有应用。

内容

Ed的天使

Ed Angel是我在加州理工学院和新墨西哥州的老朋友。埃德著有一套受欢迎的教科书关于计算机图形，现在已经达到了第八版。这些书讲述了OpenGL编程语言从Silicon Graphics到WebGL和JavaScript的演变过程。艾德在做一个MATLAB版本，我在瞎扯。

两个维度

二维的生活很容易。平面上的一个点很容易用它的笛卡尔坐标$(x,y)$，或者极坐标$(r，\theta)$，或者一个复数$z$来描述。点绕原点的旋转很容易用笛卡尔坐标乘以一个2 × 2的正交矩阵来描述，或者用极角的增量来描述，或者用$z$乘以另一个复数来描述。

三个维度

三维的情况更复杂。有笛卡尔坐标$(x,y,z)$，或者球坐标$(r，\theta，\psi)$。但是单复数的三维模拟是什么呢?旋转更加复杂。它们需要说明旋转轴和角度。有很多3 × 3的正交矩阵可以产生旋转来选择。

威廉·罗文汉密尔顿

威廉·罗文·汉密尔顿(William Rowan Hamilton, 1805-1865)，爱尔兰数学家，都柏林三一学院教授，爱尔兰皇家天文学家。他的名字与数学和物理学中的重要概念联系在一起。像他那个时代的许多其他数学家一样，他试图通过添加第二个复单位来概括二维复数，但没有成功。1846年，他意识到他实际上需要添加三个复杂的单位，$i$， $j$和$k$。

点与叉积下载188bet金宝搏

哈密尔顿四元数算法的关键成分是点积和叉积。下载188bet金宝搏点积，也被称为内积，是线性代数在任何维数中的一个常见特征。两个向量的点积是一个标量。

$ $ \ cdot b = a_1 b_1 \ + \ a₂b_2 \ \ a_3 b_3 $ $

外积只在三维空间中定义。两个向量的叉乘是第三个向量，垂直于前两个向量张成的平面。如果$i$， $j$和$k$是三维坐标轴的单位向量，那么向量$a$和$b$的叉积是

$ $ \ b = (a₂b_3 a_3 b_2) \ \ + \ (a_3 b_1 - a_1 b_3) \ j \ + \ (a_1 b_2 - a₂b_1) \ k $ $

这是叉乘的快照。

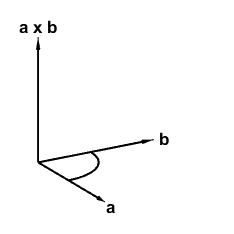
垂直于由$a$和$b$张成的平面的向量有两个可能的方向。传统的选择是由这张瑞士纸币上的右手法则和Facebook公司办公室标志上的表情符号做出的。

四元数

四元数$q$由两部分组成，标量$s$和矢量$v$。标量是一个实数;把$s$看成是标量单位$1$的系数。向量由三个实数组成;它们是三个虚单位$i$， $j$和$k$的系数。所以

$ $ q = [s, v] = s 1 \ \ + v_1 \ + v_2 j \ \ v_3 k $ $

四元数乘法的定义是，每个虚单位都是$-1$的平方根。

$ i^2 = -1, j^2 = -1, k^2 = -1

此外，这三个单元通过其产物的循环性质相互联系。下载188bet金宝搏

$ ij = k， \ \ jk = i， \ \ ki = j $

这些属性意味着

$ k = -k， \ \ kj = -i， \ \ ik = -j $

我们把$i$， $j$和$k$的这些性质称为“汉密尔顿法则”。

四元数增加

假设我们有两个四元数。

$ $ p = [r u] = r 1 \ + \ u_1 \ + u_2 j \ \ u_3 k $ $

$ $ q = [s, v] = s 1 \ \ + v_1 \ + v_2 j \ \ v_3 k $ $

加法是显而易见的。

$ p + q = [r+s, u+v] $

四元数乘法

四元数乘法既巧妙又复杂。

$ $ p q = (r + u_1 i + u_2 j + u_3 k) (s + v_1 i + v_2 j + v_3 k) $ $

每个括号里有4项，所以乘积里有16项。小心扩展，因为$i$， $j$和$k$不通勤。运用汉密尔顿法则，$i^2 = -1$， $i j = k$， $j i = -k$，等等。这16项可以这样安排。

$ $ p q = [\ r s - (u_1 v_1 + u_2 v_2 + u_3 v_3) \, $ $

$$ \ \ \ \ \ \ \ \ r(我+ v_2 j + v_1 v_3 k + s (u_1 i + u_2 j + u_3 k) \ + (u_2 v_3——u_3 v_2) i + (u_3 v_1 u_1 v_3) j + (u_1 v_2 - u_2 v_1) k \] $ $

我们认识两个熟悉的量，点积和叉积。下载188bet金宝搏

$ u \cdot v = u_1 v_1 + u_2 v_2 + u_3 v_3 $

$ $ u、v = (u_2 v_3——u_3 v_2) i + (u_3 v_1 u_1 v_3) j + (u_1 v_2 - u_2 v_1) k $ $

所以结果是

$ p q = [r s - u \cdot v, r v + s u + u \times v] $$

这是汉密尔顿对四元数乘积的定义。

单位$i$， $j$和$k$的标量部分等于0，向量部分等于[1,0,0]，[0,1,0]和[0,0,1]。例如，将它们插入产品定义中，

$ $ ^ 2 = [0 - i \ cdot我0 + 0 + i \ *我]= 1 $ $,

$ ij = [0 - 0,0 + 0 + ij] = k $$

和

$ I = - k $，即$ I = - k $，即$ I = - k $

美中不足的科学

卡佩拉科学是一个Patreon YouTube频道。https://www.patreon.com/acapellascience．

2016年，Capella Science制作了一个视频，视频中有两个汉密尔顿，一个是非常受欢迎的百老汇音乐剧《汉密尔顿》，另一个是爱尔兰数学家汉密尔顿。https://www.youtube.com/watch?v=SZXHoWwBcDc．下面是视频中的一帧截图。

本考察团

MATLAB的2021a和2021b版本包括a四元数对象，该对象在几个导航工具箱之间共享。

艾德和我有了更基本的目标，本考察团．

帮助本考察团

四元数的基本构造函数。qtn(a,b,c,d) qtn(a，[v1 v2 v3]) qtn(a)方法+ p + q - p -q uminus -q mtimes p*q ml除p\q mr除p/q mpower q^n inv(q) norm(q) disp(q)函数rot Euler randq qtn_examples注释:所有角度都是度数。该对象没有向量化。文档doc qtn在帮助浏览器中发布的输出

最重要的本考察团方法为四元数积。我认为这段代码很优雅。

dbtype89:96本考察团

89函数r = mtimes(p,q) 90% p*q 91 p = qtn(p);92 q = qtn(q);93 r.s = p.s*q。s -点(p.v,无论如何);94 r.v = p.s*q。v p + q *。v +十字架(p.v,无论如何);95 r = qtn(r);96年结束

整个本考察团类定义只有大约150行长。

基本

这里有一些基本的四元数对象的例子和测试。

两个单位。

I = qtn(0，[1 0 0]) j = qtn(0，[0 1 0])

I = 0 + 1i + 0j + 0k j = 0 + 0i + 1j + 0k

他们的产品是第三个单元。

k = i * j

K = 0 + 0i + 0j + 1k

这三个都是-1。

Ijk = i*j*k = i^2 ii = i*i

Ijk = -1 + 0i + 0j + 0k = -1 + 0i + 0j + 0k = -1 + 0i + 0j + 0k

随机

两个随机本考察团的系数为整数

P = randq q = randq

P = 2 + 8i - 1j + 4k q = 0 + 4i - 6j + 7k

加法。

P_plus_q = p + q

P_plus_q = 2 + 12i - 7j + 11k

乘法。

pq = p *

Pq = -66 + 25i - 52j - 30k

正确的部门。

r = pq / p

R = 0 + 9.6i + 2j - 2.2k

左部。p \ * p (p * q / p)应该在舍入误差范围内问．

Test1 = norm(p\r*p - q)

test1 = 4.4409 e-16

旋转

类型腐烂

函数r = rot(theta,v) % rot r = rot(theta,v)是角旋转%的四元数(qtn)，以角度表示，绕轴v旋转v = v/范数(v);R = qtn(cosd(theta)， sind(theta)*v);结束

随机的旋转轴。

v = randn(1、3)

V = -0.1241 1.4897 1.4090

绕旋转36度v。

r =腐烂(36 v)

R = 0.809017 - 0.0355214i + 0.426247j + 0.403167k

36度旋转重复10次就是360度旋转，这应该在四元数乘法恒等式的舍入误差范围内。

E = qtn(1) test2 = norm(r^10 - E)

E = 1 + 0i + 0j + 0k

代码

(2021年9月11日增补)。你可以得到代码本考察团以及这些链接中的相关功能:qtn.m，rot.m，Euler.m，randq.m，qtn_examples_1.m．

获取MATLAB代码

发布与MATLAB®R2021b