分散插值的数据缩放

发布的罗兰美国舒尔，2019年2月4日

63次观看(过去30天)|0喜欢|7评论

今天的客座博主是Josh Meyer, MATLAB数学和大数据团队的技术作家。他将讨论在离散数据插值中遇到的一个常见问题，以及如何解决它!

内容

这个问题

在对分散的数据执行插值时可能出现的一个常见问题是，得到的函数曲面的质量似乎比您预期的要低。例如，当曲面似乎没有通过所有的样本数据点时。这篇文章探讨了分散数据的缩放如何以及为什么会影响插值结果。

让我们直接进入一个例子，这样你就能明白我在说什么。想象一下，您只是从传感器收集数据，在几个点上对一些值进行采样。最终，你想要将一个曲面与数据拟合，这样你就可以在没有数据的点上近似底层函数的值。所以，你从绘图开始。

rng默认的X =兰特(500,1)/100;Y = 2.*(rand(500,1)-0.5).*90;瓦尔斯= (x.*100).^2;ptColor = [.]6 .07 .07];plot3 (x, y,瓦尔斯,“。”，“颜色”，ptColor) grid xlabel(“x”) ylabel (“y”) zlabel (“v (x, y)”)标题(“分散的数据点”）

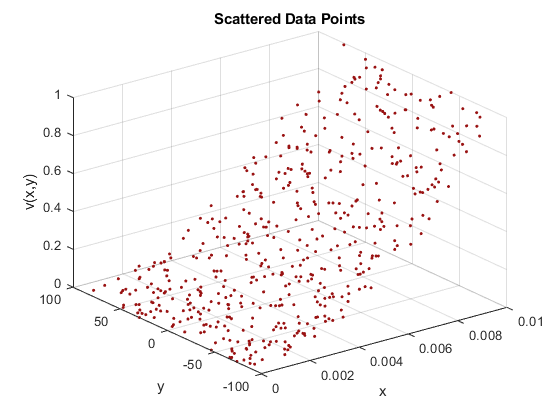
接下来，使用scatteredInterpolant为数据创建插值。这将为观测点计算插值函数，允许您在其凸包内的任何位置查询该函数。您可以创建一个查询点网格，计算这些点上的插值，并绘制函数曲面。全部完成!

F = scatteredInterpolant(x,y,vals);X = linspace(min(X)，max(X)，25);Y = linspace(min(Y)，max(Y)，25);[xq, yq] = meshgrid(X,Y);zq = F(xq,yq);持有在三色= [0.68 0.88 0.95];冲浪(xq, yq zq、“FaceColor”,三色)从包含(“x”) ylabel (“y”) zlabel (“v (x, y)”)标题(“带插值曲面的分散数据”）

．.．但是等等，结果绝对不是你想要的!表面上的所有这些“褶皱”是什么?为什么看起来曲面没有经过所有的点呢?插值曲面应该通过所有数据点!

在回到这个有问题的数据之前，让我们先快速转一转，讨论一下分散的数据插值。

散点插值背景

与点位置定义良好的网格插值不同，分散的数据提出了不同的挑战。要找到给定查询点的插值值，需要使用附近点的值。但是，当数据分散在各处时，如何做到这一点呢?一个点的位置不能用来预测另一个点的位置。通过比较所有点的位置来确定哪些点靠近给定的查询点并不是一种非常有效的方法。

X = [-1.5 3.2;1.8 - 3.3;-3.7 - 1.5;-1.5 - 1.3;0.8 - 1.2;3.3 - 1.5;-4.0 - -1.0;-2.3 - -0.7;0 -0.5;2.0 - -1.5; 3.7 -0.8; -3.5 -2.9; -0.9 -3.9; 2.0 -3.5; 3.5 -2.25]; V = X(:,1).^2 + X(:,2).^2; plot(X(:,1),X(:,2),的r *）

为了解决这个问题，MATLAB首先计算离散数据的Delaunay三角剖分。这将在数据点之外创建一系列三角形，这样由每个三角形的顶点创建的限定圆就不会包含任何点。计算的德劳内三角剖分是唯一的，直到平凡的对称。最好的部分是，三角测量可以很容易地查询，以确定哪些点最接近给定的查询点。

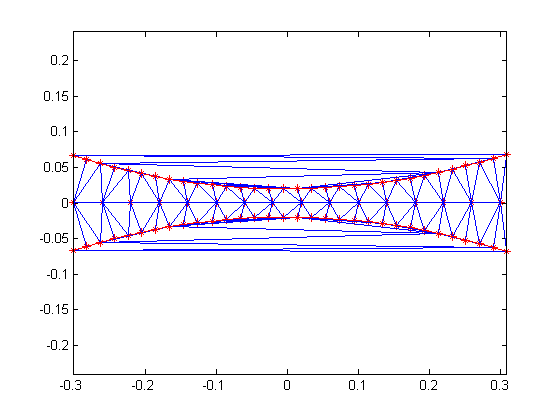
该图显示了Delaunay三角剖分和分散数据的圈定圆。请注意，红色数据点位于一个或多个限定圆的边界上，但没有一个位于其中一个圆的内部。

tr = delaunayTriangulation(X(:，1)，X(:，2));[C,r] =周心(tr);a = C(:，1);b = C(:，2);Pos = [a-r, b-r, 2*r, 2*r];持有在triplot (tr)为K = 1:长(r)矩形(“位置”pos (k,:)“弯曲”[1],“EdgeColor”三色)结束包含(“x”) ylabel (“y”)标题(分散数据的Delaunay三角测量)举行从

有了数据的三角剖分，在给定的查询点上寻找插值曲面的值就变成了查询三角剖分结构以确定哪个三角形包含查询点的问题。然后，组成该三角形顶点的数据点可用于计算在查询点处被插值曲面的值，这取决于所使用的插值方法(最近邻法、线性法等)。

该图显示了二维三角剖分中的一个查询点。为了找到这个查询点的插值值，MATLAB使用了封闭三角形的顶点。通过在许多不同的查询点重复这个计算，数据的功能面就形成了。这个功能面允许您在未收集数据的点上进行预测。

triplot (tr)在情节(X (: 1) X (:, 2),的r *) trisurf (tr.ConnectivityList X (: 1) X (:, 2), V,．.．“FaceColor”三色,．.．“FaceAlpha”，0.9)轴([- 4,4，- 4,4,0,25]);网格在plot3 (-2.6, -2.6, 0,‘* b”，“线宽”, 1.6) plot3([-2.6 - -2.6],[-2.6 - -2.6],[0 13.52]”,“- b”，“线宽”, 1.6)从视图(322.5,30);文本(-2.0,-2.6,Xq的，．.．“FontWeight”，“大胆”，．.．“HorizontalAlignment”，“中心”，．.．“写成BackgroundColor”，“没有”）;包含(“x”) ylabel (“y”) zlabel (“v (x, y)”)标题(“查询点插值”）

回到问题

现在我们知道scatteredInterpolant使用数据的Delaunay三角剖分来进行计算，让我们检查一下我们在插值时遇到麻烦的数据的底层三角剖分。

tri = delaunayTriangulation(x,y);triplot(三)在情节(x, y,的r *)举行从包含(“x”) ylabel (“y”)标题(“原始数据三角化”）

真是一团糟!合理的三角形只有几个小口袋，大多数三角形又长又细，连接点彼此相距很远。它看起来像三角测量做通过所有的数据点，而我们之前看到的糟糕的插值表面没有。我们期望插值后的曲面看起来更好。

基于这种三角划分，MATLAB有一项不令人羡慕的工作，即确定每个查询点位于那些又长又细的三角形中的哪一个。这就使我们……

问题的原因

差的插值结果是由数据的不同尺度(x轴范围为[0,0.01]，y轴范围为[- 100,100])和三角剖分中产生的又长又细的三角形造成的。MATLAB将查询点划分为对应的三角形后，利用三角形顶点求插值曲面的值。由于长而薄的三角形的顶点彼此相距很远，这导致插值曲面的局部值基于远处点的值，而不是相邻点的值。

这是一个动图，展示了三角剖分的情况x-data被缩放，而y-data是常量。一开始定义明确的三角形划分很快就变成了许多又长又细的三角形。

数据实际上是沿着x轴被挤进一个越来越小的区域。如果坐标轴保持相等，上面的动画看起来像这样。

显然，支撑分散插值计算的三角剖分对数据的扭曲很敏感。该算法期望x, y-坐标之间相对合理地缩放。但是,为什么?

这种行为源于Delaunay三角剖分算法中使用的限定圆。当您向一个方向挤压数据时，您实际上是在改变被限定圆的半径。从极端的角度来看，当点被挤压在一起并在一维中成为一条直线时，由于与圆心等距的点的轨迹成为一条直线，被限定圆的半径将趋于无穷大。三角形的分布越来越多地取决于三角形中各点的接近程度y方向，这就是为什么有接近的点y价值观却非常不同x值变成三角形顶点。

如果我们将限定的圆添加到上面的动画中，您可以看到随着数据被压缩，圆的半径会增大。

正常化拯救

这个问题的解决方案通常是通过规范化去除数据中的扭曲。归一化可以在三角剖分有许多薄三角形的情况下提高插值结果，但在其他情况下，它会损害解的精度。是否使用归一化是根据所插入数据的性质做出的判断。

好处:当自变量具有不同的单位和本质上不同的尺度时，将数据归一化可以潜在地改善插值结果。在这种情况下，将输入缩放到相似的大小可能会改善插值的数值方面。标准化将是有益的一个例子是如果x表示发动机转速(rpm, 500 ~ 3500)，和y表示从0到1的发动机负载。天平x而且y相差几个数量级，它们有不同的单位。

注意事项:如果自变量具有相同的单位，即使变量的尺度不同，在规范化数据时也要谨慎。对于相同单位的数据，归一化通过添加方向偏差而扭曲了解决方案，这影响了潜在的三角测量，并最终损害了插值的准确性。归一化是错误的一个例子是如果两者都是x而且y表示位置并使用米为单位。扩展x而且y不建议使用不相等的方法，因为正东10米在空间上应该与正北10米相同。

对于我们的问题，让我们假设x而且y有不同的单位，并标准化，使它们有相似的大小。你可以使用相对较新的正常化函数来做这个;默认情况下，它使用数据的z分数。这将转换数据，使原始平均值$\mu$变为0，原始标准差$\sigma$变为1:

$$x' = \frac{\left(x - \mu\right)}{\sigma}.$$

这种归一化非常常见，也被称为标准化．

X = normalize(X);Y = normalize(Y);

现在数据是标准化的，让我们看一下三角测量。

tri = delaunayTriangulation(x,y);triplot(三)在情节(x, y,的r *)举行从包含(“x”) ylabel (“y”)标题(“规范化数据的三角化”）

这样好多了!这些三角形大多都很清晰。只有在边缘处有几个又长又细的三角形。现在我们来看看离散插值曲面。

X = linspace(min(X)，max(X)，25);Y = linspace(min(Y)，max(Y)，25);[xq, yq] = meshgrid(X,Y);F = scatteredInterpolant(x,y,vals);zq = F(xq,yq);plot3 (x, y,瓦尔斯,“。”，“颜色”ptColor)举行在冲浪(xq, yq zq、“FaceColor”,三色)从网格在包含(“x”) ylabel (“y”) zlabel (“v (x, y)”)标题(“用插值曲面归一化数据”）

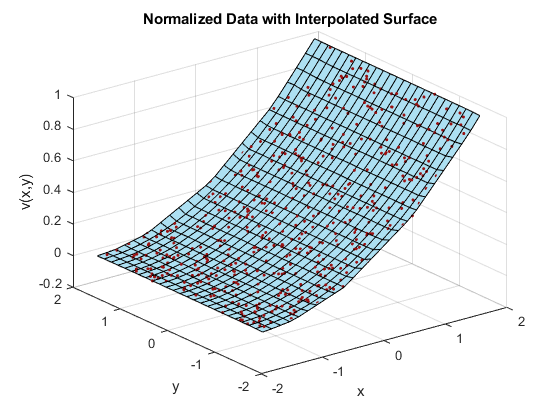
在这种情况下，将样本点归一化是可行的scatteredInterpolant计算一个更好的三角剖分，从而得到一个更好的内插曲面。

数据扩展

规范化只是数据伸缩的一种形式。通过归一化，你可以改变数据分布的形状，并改变平均值的位置。

你也可以重新调节数据，改变其最大和最小值的范围(例如，使0为最小值，1为最大值)。当您重新缩放数据时，您将保留分布的形状，但沿数轴挤压或扩展它。这改变了平均值，但保留了标准差。

数据伸缩性是需要注意的重要问题。如果数据没有适当地缩放，可能会隐藏数据中的关系或扭曲它们的强度。某些算法的结果可能会根据所使用的精确缩放而有很大差异。我们刚刚看到了分散数据的三角化是如何对缩放敏感的，但它也会在其他算法中引起问题。例如，机器学习算法通常依赖于点之间的欧几里得距离，因此它们对数据的缩放很敏感。如果没有适当的缩放，与其他特性相比，某些特性的贡献会太大，从而扭曲结果。

但这是一个广泛的话题，最好在另一篇文章中讨论!