Will's pick this week isRootFinding DemobyTeja Muppirala.

Teja is making a comeback after his 2011Sudoku Pick of the Week. This time, he has created a wonderful little Newton-Raphson app. For anyone who's taken a numerical methods class, you are probably familiar with this technique for finding a value forxthat satisfies equationf(x) = 0. But if you're new to the concept, Wikipedia has agreat articleon the subject.

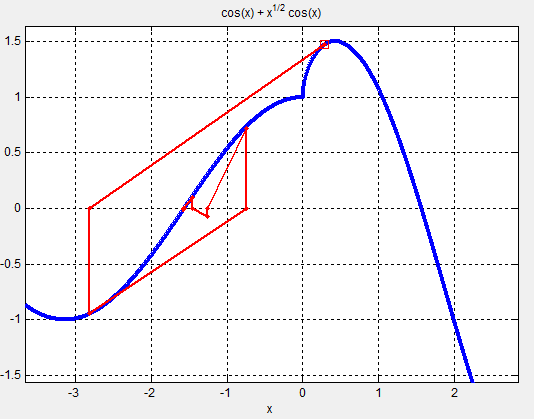
In essence, this algorithm starts with an initial guess for the value ofx. Iff(x)equals zero, then lucky you, you're done. If not, you calculate the derivative of the function and use that to aim yourself towards a better guess for the value ofx. You repeat this process with your new value ofx, and after a few iterations, you hopefully converge onf(x) = 0. In the image below, you see how we approach the zero-crossing of the blue line (ourf(x)) with several Newton-Raphson iterations (the red lines).



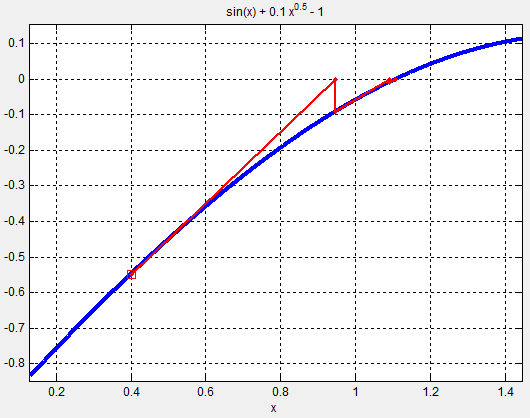
It turns out that this is a screenshot from Teja's root finding app. The user interface enables you to symbolically express your equation. You specify your initial guess and number of iterations; the app will then present you the solution. What's really fun about this is that you can click on the figure and instantaneously get results for a new initial guess. This interaction is quite instructive in the effectiveness yet limitations of this root finding method. I enjoyed experimenting with functions that weren't continuously differentiable. Oftentimes, my results would be unstable, but every once in a while, I could still achieve convergence.



Comments
Let us know what you thinkhereor leave acommentfor Teja.