使用线性规划最大化长期投资：基于问题

打开生活的脚本

这个例子展示了如何使用基于问题的方法来解决一个在固定年限内具有确定性回报的投资问题T．问题是要把你的钱分配到可用的投资上，以最大化你的最终财富。关于基于求解器的方法，请参见利用线性规划最大化长期投资:基于求解器．

问题公式化

假设你有一笔初始资金Capital_0投资一段时间T年N零优惠券。每个债券每年支付固定利率，复合投资，并在到期期结束时支付校长加复合利息。目标是最大限度地提高金额T年。

您可以包含一个约束条件，即在进行投资时，单个投资不能超过总资本的某个部分。

这个例子首先给出了小情况下的问题设置，然后给出了一般情况。

你可以将其建模为线性规划问题。因此，为了优化你的财富，用优化问题的方法来制定问题。

介绍性的例子

从一个小例子开始:

投资的起始金额Capital_0是1000美元。
时间段T是5年。
债券的数量N是4。
为了模拟未成币的资金，每年有一个选择B0，其成熟期为1年，利率为0％。
债券1，用B1表示，可以在第一年购买，期限为4年，利率为2%。
债券2，用B2表示，可以在第5年购买，期限为1年，利率为4%。
BOND 3由B3表示，可以在2年级购买，具有4年的到期期，利率为6％。
债券4，用B4表示，可以在第二年购买，期限为3年，利率为6%。

将第一个选项B0分为5个期限为1年，利率为0的债券，这个问题可以等价地建模为总共有9个可用债券，这样k = 1..9

条目k矢量图购买日期代表着年初的那份债券k可供购买。
条目k矢量图成熟代表到期期 $米_{k}$ 的债券k．
条目k矢量图MaturityYears代表年底的债券k可供出售。
条目k矢量图银行利率代表百分比利率 $ρ_{k}$ 的债券k．

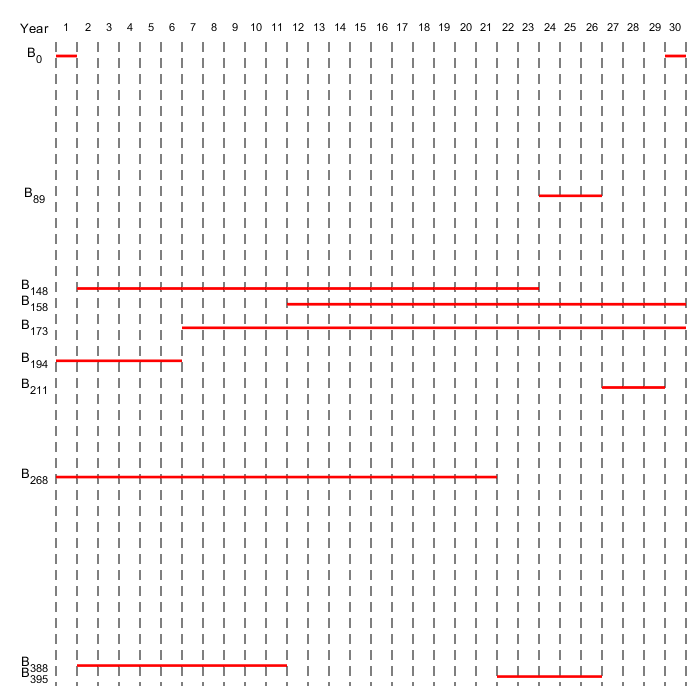
通过水平杆可视化此问题，该问题代表每个键的可用购买时间和持续时间。

%以年为单位的时间段T = 5;%债券数量n = 4;％初始金额Capital_0 = 1000;%购买机会总数nptotal = n + t;%购买时间PurchaseYears =[1; 2; 3; 4、5、1;5;2;2);%债券期限成熟= [1; 1; 1; 1; 1; 4; 1; 4; 3];债券发售时间成熟years =购买日期+成熟 -  1;％利率百分比利率= (0,0,0,0,0;2,4,6,6];%一年的利息后的回报rt = 1 +利息/100;plotInvestments (N, PurchaseYears,成熟,利率)

决策变量

用向量表示决策变量x，在哪里x (k)投资债券的金额是多少k,因为k = 1,…,9．到期时，投资所得x (k)是

$x （ k ）（ 1 + ρ_{k} / 100 ）^{米_{k}} ．$

定义 $β_{k} ＝ 1 + ρ_{k} / 100$ 和定义 $r_{k}$ 作为债券的总回报k：

$r_{k} ＝（ 1 + ρ_{k} / 100 ）^{米_{k}} ＝ β_{k}^{米_{k}} ．$

x = optimvar (“x”，nptotal，'indowbound', 0);%总回报率r = rt ^成熟;

目标函数

他们的目标是选择投资项目，使年底的收益最大化T．从图中，你可以看到投资在不同的中期收集并再投资。在年底T，从投资5、7和8中收回的钱可以收集起来，代表你的最终财富:

$\underset{x}{马克斯} x_{5} r_{5} + x_{7} r_{7} + x_{8} r_{8}$

创建一个最大化的优化问题，并包含目标函数。

兴趣重量= OptimProblem（“ObjectiveSense”，'最大化'）;emperprob.objective = x（5）* r（5）+ x（7）* r（7）+ x（8）* r（8）;

线性约束:投资不要超过你所拥有的

每年，您都有一定数量的资金可以购买债券。从第1年开始，您可以在购买选项中投资初始资本 $x_{1}$ 和 $x_{6}$ ,所以:

$x_{1} + x_{6} ＝ {C 一个 p 我 t 一个 l}_{0}$

然后在接下来的几年里，你从到期债券中收集收益，并将它们再投资于新的可用债券，从而得到方程组:

$\begin{array}{ll} x_{2} + x_{8} + x_{9} & ＝ r_{1} x_{1} \\ x_{3.} & ＝ r_{2} x_{2} \\ x_{4} & ＝ r_{3.} x_{3.} \\ x_{5} + x_{7} & ＝ r_{4} x_{4} + r_{6} x_{6} + r_{9} x_{9} \end{array}$

investconstr = optimconstr (T, 1);investconstr(1) = x(1) + x(6) == Capital_0;investconstr (2) = x (2) + (8) + x (9) = = r (1) * x (1);Investconstr (3) = x(3) == r(2)*x(2);Investconstr (4) = x(4) == r(3)*x(3);investconstr (5) = (5) + x (7) = = r (4) * x (4) + r (6) * x (6) + r (9) * x (9);interestprob.Constraints.investconstr = investconstr;

约束约束:无借款

因为投资的每一项都必须是正的，溶液向量中的每一项 $x$ 必须是积极的。通过在解向量上设置一个下界来包含这个约束 $x$ ．解向量没有明确的上界。

x.LowerBound = 0;

解决这个问题

解决这个问题，不要限制你可以投资债券的金额。内点算法可用于求解这类线性规划问题。

选项= Optimoptions（“linprog”，'算法'，'内点'）;[溶胶,fval exitflag] =解决(interestprob,'选项'选项)

使用linprog解决问题。在解决过程中找到的解决方案。

sol =结构体字段:x (9 x1双):

fval = 1.2625e + 03

ExitFlag = OptimalAllyolution.

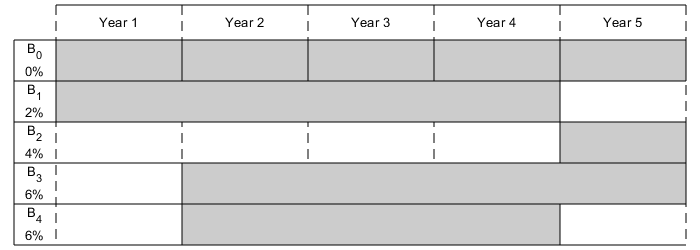
可视化解决方案

退出标志表明求解器找到了最优解。的值fval，作为第二个输出参数返回，对应于最终财富。看看最终投资和随着时间的推移投资分配。

流('在％d年后，初始$％g的回报是％g \ n'，．..t，capital_0，fval）;

5年后，最初1000美元的回报率是1262.48美元

plotInvestments (N, PurchaseYears、成熟度、利率、sol.x)

拥有有限持有的最佳投资

为了分散您的投资，您可以选择将投资于任何债券的金额限制在一定的百分比PMAX.当年的总资本（包括当前期限内的债券退还）。您获得以下不等式系统：

$\begin{array}{ll} x_{1} & \leq P 米一个 x \times {C 一个 p 我 t 一个 l}_{0} \\ x_{2} & \leq P 米一个 x \times （ β_{1} x_{1} + β_{6} x_{6} ） \\ x_{3.} & \leq P 米一个 x \times （ β_{2} x_{2} + β_{6}^{2} x_{6} + β_{8} x_{8} + β_{9} x_{9} ） \\ x_{4} & \leq P 米一个 x \times （ β_{3.} x_{3.} + β_{6}^{3.} x_{6} + β_{8}^{2} x_{8} + β_{9}^{2} x_{9} ） \\ x_{5} & \leq P 米一个 x \times （ β_{4} x_{4} + β_{6}^{4} x_{4} + β_{8}^{3.} x_{8} + β_{9}^{3.} x_{9} ） \\ x_{6} & \leq P 米一个 x \times {C 一个 p 我 t 一个 l}_{0} \\ x_{7} & \leq P 米一个 x \times （ β_{4} x_{4} + β_{6}^{4} x_{4} + β_{8}^{3.} x_{8} + β_{9}^{3.} x_{9} ） \\ x_{8} & \leq P 米一个 x \times （ β_{1} x_{1} + β_{6} x_{6} ） \\ x_{9} & \leq P 米一个 x \times （ β_{1} x_{1} + β_{6} x_{6} ） \end{array}$

以任何债券投资的最大百分比最大百分比Pmax = 0.6;constrlimit = optimconstr (nPtotal, 1);constrlimit(1) = x(1) <= Pmax*Capital_0;constrlimit (2) = x (2) < = Pmax * (rt (1) * x (1) + rt (6) * x (6));constrlimit (3) = x (3) < = Pmax * (rt (2) * x (2) + rt (6) ^ 2 * x (6) + rt (8) * * (8) + rt (9) * x (9));constrlimit (4) = x (4) < = Pmax * (rt (3) * x (3) + rt (6) ^ 3 * x (6) + rt (8) ^ 2 * x (8) + rt (9) ^ 2 * x (9));constrlimit (5) = x (5) < = Pmax * (rt (4) * x (4) + rt (6) ^ 4 * x (6) + rt (8) ^ 3 * x (8) + rt (9) ^ 3 * x (9));constrlimit(6) = x(6) <= Pmax*Capital_0;constrlimit (7) = x (7) < = Pmax * (rt (4) * x (4) + rt (6) ^ 4 * x (6) + rt (8) ^ 3 * x (8) + rt (9) ^ 3 * x (9));constrlimit (8) = x (8) < = Pmax * (rt (1) * x (1) + rt (6) * x (6)); constrlimit(9) = x(9) <= Pmax*(rt(1)*x(1) + rt(6)*x(6)); interestprob.Constraints.constrlimit = constrlimit;

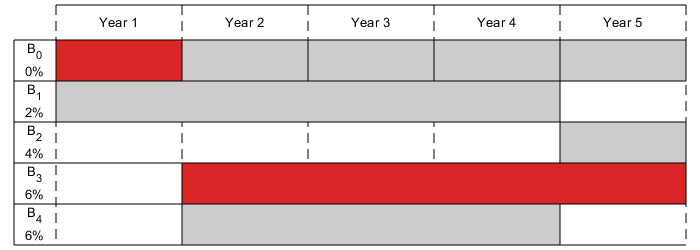
解决这个问题的方法是在任何一种资产上的投资不要超过60%。绘制购买结果。注意，如果没有这个限制，你的最终财富将少于投资。

[溶胶,fval] =解决(interestprob,'选项'，选项）;

使用linprog解决问题。最低发现满足约束。优化完成，因为目标函数在可行的方向上是非减小的，以便在功能公差的所选值内，并且对约束公差的所选值满足约束。

流('在％d年后，初始$％g的回报是％g \ n'，．..t，capital_0，fval）;

5年后，最初1000美元的回报率是1207.78美元

plotInvestments (N, PurchaseYears、成熟度、利率、sol.x)

任意尺寸模型

为问题的一般版本创建一个模型。说明使用T= 30年，400个随机产生的债券，利率为1％至6％。此设置导致具有430个决策变量的线性编程问题。

重复性的％rng默认的％初始金额Capital_0 = 1000;%以年为单位的时间段T = 30;%债券数量n = 400;%购买机会总数nPtotal = N + T;%生成随机的期限成熟= randi（[1 t-1]，nptotal，1）;债券1的到期日为1年成熟度(1:T) = 1;为每个债券随机生成年利率利率=兰迪(6 nPtotal 1);债券1的利率为0(不投资)利率(1:T) = 0;%一年的利息后的回报rt = 1 +利息/100;计算每只债券在到期时的收益:r = rt ^成熟;%为每个选项生成随机购买年份PurchaseYears = 0 (nPtotal, 1);每年都可以购买% Bond 1购买日期（1：T）= 1：T;为i = 1: N%随机生成债券在年底前到期的年份％t年购买日期（I + T）= RANDI（[1 T-Perurity（I + T）+1]）;结束计算每只债券在年底到期的年份成熟years =购买日期+成熟 -  1;

计算债券可以买卖的时间。的BuyIndex.矩阵持有潜在的购买时间，以及sellindex矩阵持有每个键的潜在销售时间。

buyindex = false (nPtotal T);%分配nPtotal-by-T矩阵为II = 1：T BuyIndex（：，ii）=购买== II;结束sellindex = false (nPtotal T);为ii = 1:T sellindex(:，ii) =到期日;结束

建立与化学键对应的优化变量。

x = optimvar (“x”，nptotal，1，'indowbound', 0);

建立优化问题和目标函数。

兴趣重量= OptimProblem（“ObjectiveSense”，'最大化'）;interestprob。目标=总和(x (sellindex (:, T))。* r (sellindex (:, T)));

为了方便起见，创建一个临时数组xBuy，其中的列表示我们在每个时间段可以购买的债券。

xbuy = repmat（x，1，t）。* Double（BuyIndex）;

类似地，创建一个临时数组xSell，其列表示我们在每个时间段可以出售的债券。

xSell = repmat (x 1 T)。*双(sellindex);

出售这些界限所产生的回报是

xReturnFromSell = xSell。* repmat (r, 1, T);

设定一个约束条件，即你在每个时间段的投资金额是你在上一个时间段卖出的金额。

exingprob.constraints.initialinvest = sum（xbuy（：，1））== capital_0;exingProb.Constraints.investConstraint = sum（xbuy（：，2：t），1）== sum（xreturnfromsell（：，1：t-1），1）;

无Holding Limit的解决方案

解决这个问题。

Tic [sol,fval,exitflag] = solve(兴趣问题，'选项'，选项）;

使用linprog解决问题。最低发现满足约束。优化完成，因为目标函数在可行的方向上是非减小的，以便在功能公差的所选值内，并且对约束公差的所选值满足约束。

toc

运行时间为0.256259秒。

这些投资做得怎么样?

流('在％d年后，初始$％g的回报是％g \ n'，．..t，capital_0，fval）;

30年后，最初1000美元的回报率是5167.58美元

有限持有的解决方案

为了限制每种资产的投资比例，可以建立一个矩阵，跟踪每次活跃债券的情况。以表示每个投资必须小于的约束PMAX.乘以总价值，建立一个矩阵，记录每次投资的价值。对于这个更大的问题，将最大分数设置为0.4。

Pmax = 0.4;

创建一个活跃的对应于债券可持有时间的矩阵，以及cactive持有每一活跃债券的累积期限的矩阵。债券的价值j在时间t是x（j）*（rt ^ cactive）．

Active = double(buyindex | sellindex);为ii = 1:T active(:，ii) = double((ii >= PurchaseYears & (ii <=到期日)));结束cactival = cumsum（活性，2）;cactivent = cactivent。*活跃;

创建矩阵，其条目(j,p)表示债券j在时间段p的值:

bondValue = repmat (x 1 T)。*活跃。* (rt ^ (cactive));

确定每个时间间隔的投资总额，这样您就可以对有限的持股施加约束。mvalue钱是否投资于每次期间结束时的所有债券nPtotal-经过-TMatrix.Moneyavaulable是在时间段开始投资的金钱键的总和，这意味着每次投资组合的价值。

constrlimit = optimconstr (nPtotal T);constrlimit(:，1) = xBuy(:，1) <= Pmax*Capital_0;constrlimit (:, 2: T) = xBuy (:, 2: T) < = repmat (Pmax *总和(bondValue (:, 1: T - 1), 1), nPtotal, 1)。*双(buyindex (:, 2: T));interestprob.Constraints.constrlimit = constrlimit;

用有限的资金解决问题。

Tic [sol,fval,exitflag] = solve(兴趣问题，'选项'，选项）;

使用linprog解决问题。最低发现满足约束。优化完成，因为目标函数在可行的方向上是非减小的，以便在功能公差的所选值内，并且对约束公差的所选值满足约束。

toc

经过的时间是1.197712秒。

流('在％d年后，初始$％g的回报是％g \ n'，．..t，capital_0，fval）;

30年后，最初的1000美元的回报是5095.26美元

为了加快求解速度，请尝试双单纯形算法。

选项= Optimoptions（“linprog”，'算法'，'双重simplex'）;Tic [sol,fval,exitflag] = solve(兴趣问题，'选项'，选项）;

使用linprog解决问题。找到最佳解决方案。

toc

运行时间为0.514705秒。

流('在％d年后，初始$％g的回报是％g \ n'，．..t，capital_0，fval）;

30年后，最初的1000美元的回报是5095.26美元

在这种情况下，双单位算法需要更少的时间来获得相同的解决方案。

定性结果分析

为了感受溶液，将其与量进行比较Fmax.如果你能把所有的初始资金以6%的利率(最高利率)投资于30年的债券，你就能得到。你也可以根据你的最终财富计算相应的利率。

%最大数量fmax = capital_0 *（1 + 6/100）^ t;％比率（百分比）老鼠= fval / fmax * 100;%等值利率(以百分比为单位)rsol = ((fval / Capital_0) ^ (1 / T) 1) * 100;流(['收集的金额为最高金额的％g％．..“你会从投资中获得一个债券。\ n'．..“你的最终财富相当于%g%%利率在%d年”．..“。\ n”]，大鼠，Fmax，RSOL，T）

已收回的金额是你投资于一个债券可获得的最高金额5743.49美元的88.7137%。你的最终财富相当于30年期间5.57771%的利率。

PlotInforcements（n，购买日期，成熟，有趣，sol.x，false）