旅行推销员问题：基于问题

打开生活的脚本

这个例子展示了如何使用二进制整数规划来解决经典的旅行商问题。这个问题涉及到通过一组站点(城市)找到最短的封闭路线(路径)。在这种情况下，有200个站点，但你可以很容易地改变nstops.变量以获得不同的问题大小。您将解决最初的问题，并看到解决方案具有子游览。这意味着找到的最佳解决方案不会给出一条贯穿所有点的连续路径，而是有几个不相连的循环。然后，您将使用一个迭代过程来确定子路径、添加约束并重新运行优化，直到消除子路径。

对于基于求解器的方法，请参阅旅行推销员问题：基于求解器。

问题制定

制定用于整数线性编程的旅行推销员问题，如下所示：

生成所有可能的行程，意味着所有不同的站点对。
计算每次旅行的距离。
最小化的成本函数是旅游中每次旅行的旅行距离的总和。
决策变量是二进制的，并且与每个旅程相关联，其中每个1表示巡回演出中存在的行程，每个0表示不在旅游时的行程。
为确保游览包括每个停止，包括每个停止都在恰好两次旅行的线性约束。这意味着一个到达，一个到达停止。

生成停止

在一个粗糙的多边形代表美国大陆内产生随机止损

加载（'usborder.mat'那“x”那“y”那“xx”那“yy”）;RNG（3，'twister'）％在缅因州和佛罗里达州停靠，并且是可重复的nStops = 200;你可以使用任何数字，但问题的规模是N^2stopsLon = 0 (nStops, 1);％分配NSTOPS的X坐标stopslat = stopslon;％allocate y-cocordinatesn = 1;而（n <= nstops）xp = rand * 1.5;yp = rand;如果Inpolygon（XP，YP，X，Y）如果在边界内，％tteststopsLon (n) = xp;stopsLat (n) = yp;n = n + 1;结尾结尾

计算点间距离

因为有200个站点，有19,900次行程，这意味着19,900个二进制变量(# variables = 200 choose 2)。

生成所有行程，意味着所有对的停止。

IDXS = NCHOOSEK（1：NSTOPS，2）;

假设地球是平的，用勾股定理计算所有的旅行距离。

drawtext (dixs (:，1) - dixs (:，2))， color0000ff;......stopsLon (idx(: 1))——stopsLon (idx (:, 2)));lendist =长度(经销);

有了这个定义经销矢量，旅游的长度是

dist'*旅行

在哪里旅行是代表解决方案所采用的旅行的二进制矢量。这是游览您尝试最小化的距离。

创建图形和绘制地图

用图来表示这个问题。创建一个图形，其中站点是节点，行程是边。

图G = (idx (: 1), idx (:, 2));

使用图形绘图显示停止。绘制没有图形边缘的节点。

图hGraph = plot(G，'xdata'stopsLon,“YData”，stopslat，“线型”那'没有任何'那“NodeLabel”, {});抓住在％绘制外界情节(x, y,'r-')举行从

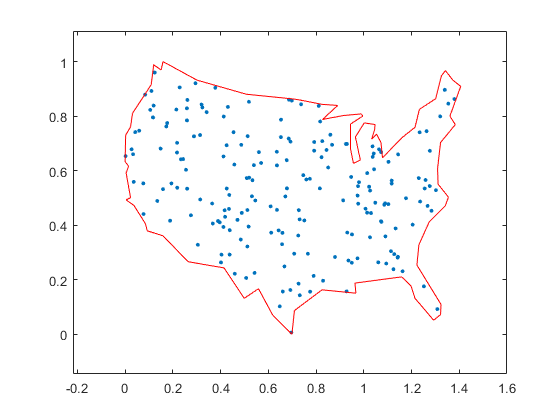
创建变量和问题

用表示潜在行程的二进制优化变量创建一个优化问题。

TSP = OptimProblem;trips = Optimvar（'旅行'，贷款人，1，“类型”那“整数”那'indowbound'0,'上行'1);

在问题中包含目标函数。

tsp。目标=距离' *旅行;

约束

创建每个停止有两个相关旅行的线性约束，因为必须有每个停止行程和行程离开每个站点。

使用图形表示法，通过找到与该停止相连接的所有边，来识别开始或结束于该停止的所有行程。对于每一站，创建约束条件，使该站的行程之和等于2。

constr2trips = optimconstr (nStops, 1);为了stop = 1:nStops wherhidxs = outedges(G,stop);识别与停车相关的行程CONSTR2TRIPS（STOP）= SUM（TRIPS（WHINDXS））== 2;结尾tsp.constraints.Constr2trips = Constr2.Rips;

解决初始问题

问题已准备好解决。要抑制迭代输出，请关闭默认显示。

opts = Optimoptions（“intlinprog”那“显示”那“关闭”）;Tspsol =解决（TSP，“选项”，选择）

tspsol =结构体字段:旅行：[19900×1双]

可视化解决方案

用解决方案行程作为边创建一个新图。为此，在某些值不是精确整数的情况下，将解四舍五入，并将结果值转换为逻辑。

tspsol.trips =逻辑（圆形（tspsol.trips））;GSOL = Graph（IDXS（Tspsol.trips，1），IDxs（Tspsol.trips，2），[]，numnodes（g））;% Gsol = graph(idxs(tspsol.trips,1)，idxs(tspsol.trips,2));%在大多数情况下也有效

覆盖现有绘图上的新图表并突出显示其边缘。

抓住在突出(hGraph Gsol,“线型”那' - ')标题('与副表的解决方案'）

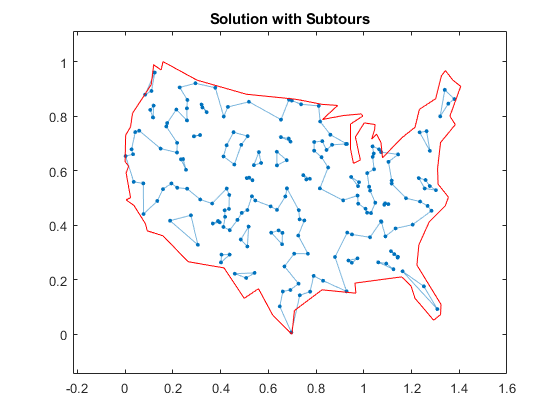
从地图上可以看到，该解决方案有几个子游览。到目前为止指定的约束并不能阻止这些子行程的发生。为了防止发生任何可能的子循环，您将需要大量的不等式约束。

子我们的限制

因为您不能添加所有的子游览约束，所以采用迭代的方法。检测当前解决方案中的子循环，然后添加不等约束以防止发生那些特定的子循环。通过这样做，您可以在几个迭代中找到合适的行程。

消除不等式约束的子学会。如果您在子台议会中有五个点，那么这是一个例子，那么你有五行连接这些点来创建子。通过实现不等式约束来说明这五点之间必须小于或等于四行，从而消除此子流。

更重要的是，找出这五个点之间的所有直线，并限制解中出现的直线不超过四条。这是一个正确的约束，因为如果一个解中存在5条或更多的直线，那么这个解就会有一个子环(一个带有 $N$ 节点和 $N$ 边缘总是包含一个循环）。

通过识别连接的组件来检测子流量Gsol，用当前解决方案中的边构建的图。conncomp返回一个向量，其中包含每条边所属的子游程的编号。

TouriDXS = Conncomp（GSOL）;numtours = max（touridxs）;％子台楼数fprintf（'# of subtours: %d\n', numtours);

小圈子数量:27个

包括线性不等式约束来消除子流，并反复调用求解器，直到只需一个子电台。

%为子游览添加的约束的索引k = 1;而numtours> 1％重复，直到只有一个子系统％添加子大楼约束为了II = 1：NumTours Insubtour =（TouriDXS == II）;当前子系统中的％边缘一个= (inSubTour (idx), 2);％完整的图形指数，两端在子大学中CONSTRNAME =.“subtourconstr”+ num2str (k);tsp.Constraints.(constrname) = sum(trips(a)) <= (nnz(inSubTour) - 1);K = K + 1;结尾再次尝试优化[TSPSOL，FVAL，EXITFLAG，输出] =求解（TSP，“选项”，选择）;tspsol.trips =逻辑（圆形（tspsol.trips））;GSOL = Graph（IDXS（Tspsol.trips，1），IDxs（Tspsol.trips，2），[]，numnodes（g））;% Gsol = graph(idxs(tspsol.trips,1)，idxs(tspsol.trips,2));%在大多数情况下也有效％plot新解决方案rugk.linestyle =.'没有任何';％删除先前突出显示的路径突出(hGraph Gsol,“线型”那' - ') drawnow％这次有多少子流？TouriDXS = Conncomp（GSOL）;numtours = max（touridxs）;％子台楼数fprintf（'# of subtours: %d\n'，numtours）结尾

分游数量:20

7个

9个

9个

二

7个

二

#分游:1

标题('消除了副表的解决方案'）;抓住从

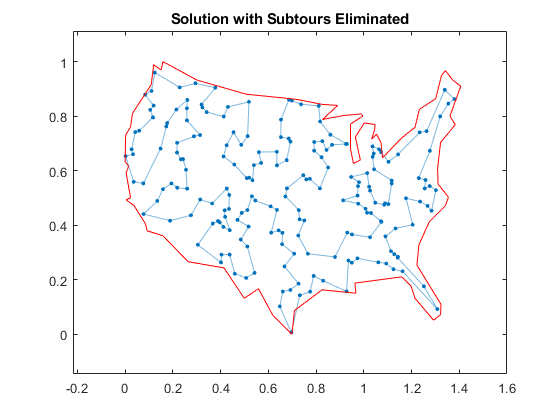
解决方案质量

该解决方案代表了可行的巡演，因为它是单个闭环。但这是一个最低的成本之旅吗？一个方法可以检查输出结构。

disp（output.absolutegap）

0.

绝对隙的小于意味着解决方案是最佳的，或者具有接近最佳的总长度。