频域线性回归

该示例示出了如何使用离散傅立叶变换来构建线性回归模型的时间系列。在这个例子中所用的时间序列是在美国意外死亡事件从1973年的月数，以1979年的数据公布在Brockwell和Davis（2006）。最初来源是美国国家安全委员会。

输入数据。复制exdata矩阵入MATLAB®工作区。

exdata = [9007 7750 8162 7717 7792 7836 8106 6981 7306 7461 6957 6892 8928 8038 8124 7776 7726 7791 9137 8422 7870 7925 8106 8129 10017 8714 9387 8634 8890 9115 10826 9512 9556 8945 9299 9434 11317 10120 10093 10078 10625 10484 10744 9823 9620 9179 93029827 9713 8743 8285 8037 8314 9110 9938 9129 8433 8488 8850 9070 9161 8710 8160 7874 8265 8633 8927 8680 8034 8647 8796 9240];

exdata是一个12×6矩阵。的每一列exdata包括12个月的数据。每列的第一行包含美国意外死亡的相应今年一月份的数量。每列的最后一行包含美国意外死亡相应年度的月数。

重塑数据矩阵划分成72×1时间系列和1973绘制数据的年到1978年。

TS =重塑（exdata，72,1）;年= linspace（1973,1979,72）;图（多年，TS，“邻”，'MarkerFaceColor'，'汽车'）xlabel（'年'）ylabel（“意外死亡数”）

的数据的目视检查表明意外死亡人数以周期性的方式变化。振荡的周期似乎是大约（一年12个月）。数据的周期性质表明，适当的模型可能是

哪里 $$\mu$$是整体平均， $$ñ$$是时间序列的长度，和 $$\epsilon （ñ）$$是独立同分布（IID）高斯随机变量的具有零均值和方差一些白噪声序列。加性噪声术语占该数据中固有的随机性。模型的参数是总体均值和余弦和正弦的幅度。该模型是线性的参数。

为了构建一个线性回归模型在时域中，必须指定要使用的频率的余弦和正弦，形成设计矩阵，并解决了正规方程，以获得模型参数的最小二乘估计。在这种情况下，它更容易使用离散傅立叶变换来检测周期性，仅保留傅里叶系数的一个子集，并且反转的变换，以获得拟合的时间序列。

执行数据的频谱分析揭示其频率在数据中的可变性显著贡献。由于信号的总平均是大约9000，并且正比于傅立叶在0频率变换，减去平均值之前的频谱分析。这减少了在0频率的大的幅度傅立叶系数，使任何显著振荡更容易检测。在傅立叶频率变换以即时间序列长度，1/72的倒数的间隔隔开。月度采样数据，在频谱分析中的最高频率为1个周期/ 2个月。在这种情况下，方便的是看谱分析在周期/年的条款，以便相应地缩放所述频率可视化。

tsdft = FFT（TS-平均值（TS））;FREQ = 0：1/72：1/2;图（频率* 12，ABS（tsdft（1：长度（TS）/ 2 + 1）），“邻”，...'MarkerFaceColor'，'汽车'）xlabel（“周期/年”）ylabel（'大小'）AX = GCA;ax.XTick = [1/6 1 2 3 4 5 6];

基于大小，1个循环/ 12个月的频率是数据最显著振荡。在1个循环/ 12个月大小超过两倍的任何其它大小。然而，频谱分析表明，也有在数据的其他周期分量。例如，似乎有周期性分量在谐波的1个循环/ 12个月（整数倍）。此外，还似乎是一个周期为1个循环/ 72个月周期分量。

基于该数据的频谱分析，适合使用余弦和正弦项的最显著分量的频率的线性回归模型的简单：1个循环/年（1个循环/ 12个月）。

确定所述离散傅里叶频率槽转换对应于1个循环/ 12个月。由于频率在1/72间隔开并且与第一仓对应于0频率，正确的二进制值是12分之72+ 1。这是的频点正频率。您还必须包括相应的频率仓负频率：-1周期/ 12个月。用MATLAB索引，负频率的频率仓是72-72 / 12 + 1。

创建零的72×1矢量。填有对应于1个循环/ 12个月一个正和负频率的傅立叶系数的矢量的适当元件。反傅立叶变换，并添加总体平均获得适合的意外死亡数据。

freqbin = 72/12;freqbins = [freqbin 72 freqbin] +1;tsfit =零（72,1）;tsfit（freqbins）= tsdft（freqbins）;tsfit = IFFT（tsfit）;亩=平均（TS）;tsfit =亩+ tsfit;

绘制原始数据使用两个傅里叶系数拟合系列一起。

图（多年，TS，“邻”，'MarkerFaceColor'，'汽车'）xlabel（'年'）ylabel（“意外死亡数”）保持上图（年，tsfit，'行宽'，2）图例（'数据'，“拟合模型”）保持离

拟合模型似乎捕获数据，并支持初步结论的数据为1年的周期振荡的一般周期性质。金宝app

为了评估的1个循环/ 12个月的单频率如何充分占观察到的时间序列，形成所述残差。如果残差类似于白噪声序列，其中一个频率的简单的线性模型已充分建模的时间序列。

为了评估残差，使用具有95％-confidence间隔自相关序列为白噪声。

渣油= TS-tsfit;[XC，滞后] = xcorr（渣油，50％，“系数_”）;茎（滞后（51：结束），XC（51：结束），'填充'）保持上lconf = -1.96 *酮（51.1）/ SQRT（72）;uconf = 1.96 *酮（51.1）/ SQRT（72）;情节（滞后（51：结束），lconf，'R'）情节（滞后（51：结束），uconf，'R'）xlabel（'落后'）ylabel（“相关系数”）标题（“残差自相关”）保持离

自相关值在一些滞后的落在95％置信区间之外。它不会出现残差是白噪声。结论是，与一个正弦分量的简单线性模型不占意外死亡人数的所有振荡。这是预期的，因为频谱分析，除了主导振荡透露额外的周期分量。创建包含由频谱分析表明将改善配合美白残差额外的周期项的模型。

适合它由三个最大的傅里叶系数大小的模型。因为你要保留相应正面和负面的频率的傅里叶系数，保留了最大的6个索引。

tsfit2dft =零（72,1）;[Y，I] =排序（ABS（tsdft），“降序”）;指数= I（1：6）;tsfit2dft（指数）= tsdft（索引）;

表明，仅保留72的傅立叶系数（3个频率）的6保留大部分的信号的能量。首先，证明，保留所有的原始信号和傅立叶之间的傅里叶系数产量能量等价变换。

范数（1 / SQRT（72）* tsdft，2）/规范（TS-平均值（TS），2）

ANS = 1.0000

的比率为1。现在，检查能量比其中仅3个频率被保留。

范数（1 / SQRT（72）* tsfit2dft，2）/规范（TS-平均值（TS），2）

ANS = 0.8991

的能量的大约90％被保留。等价地，时间序列的方差的90％是由3种频率成分占。

形成根据3个频率分量的数据的估计值。比较原始数据，具有一个频率的模型，并用3个频率模型。

tsfit2 =亩+ IFFT（tsfit2dft，“对称”）;图（多年，TS，“邻”，'markerfacecolor'，'汽车'）xlabel（'年'）ylabel（“意外死亡数”）保持上图（年，tsfit，'行宽'2）图（年，tsfit2，'行宽'，2）图例（'数据'，“1个频率”，“3个频率”）保持离

使用3个频率提高了拟合到原始信号。您可以通过检查从3频率模型的残差的自相关看到这一点。

渣油= TS-tsfit2;[XC，滞后] = xcorr（渣油，50％，“系数_”）;茎（滞后（51：结束），XC（51：结束），'填充'）保持上lconf = -1.96 *酮（51.1）/ SQRT（72）;uconf = 1.96 *酮（51.1）/ SQRT（72）;情节（滞后（51：结束），lconf，'R'）情节（滞后（51：结束），uconf，'R'）xlabel（'落后'）ylabel（“相关系数”）标题（“残差自相关”）保持离

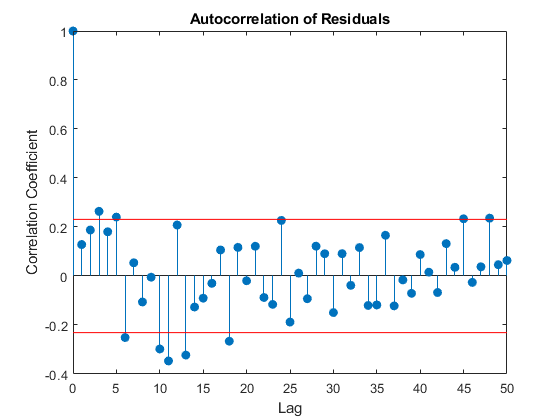
使用3个频率导致残差是更接近白噪声过程。

表明，从傅里叶获得的参数的值的变换是等效于时域的线性回归模型。查找整体平均最小二乘估计，余弦幅度，并为三个频率通过形成设计矩阵和解决正规方程的正弦振幅。比较从傅立叶变换得到的拟合时间序列。

X =酮（72.7）;X（：，2）= COS（2 * PI / 72 *（0:71））';X（：，3）= SIN（2 * PI / 72 *（0:71））';X（：，4）= COS（2 * PI *72分之6*（0:71））';X（：，5）= SIN（2 * PI *72分之6*（0:71））';X（：，6）= COS（2 * PI *72分之12*（0:71））';X（：，7）= SIN（2 * PI *72分之12*（0:71））';的β= X \ TS;tsfit_lm = X *β;MAX（ABS（tsfit_lm-tsfit2））

ANS = 7.2760e-12

这两种方法得到相同的结果。两个波形之间的差的最大绝对值为10-12的量级上。在这种情况下，频域的方法是比同等的时域方法更容易。你自然地使用频谱分析，以在视觉上检查其振荡存在于数据。从该步骤中，使用简单的傅立叶系数来构建模型由总和余弦和正弦的信号。

对于在时间序列上的频谱分析的详细信息，并与时域回归见（沙姆韦和斯托弗，2006年）的等价性。

虽然频谱分析可以回答这周期分量的数据的变化显著贡献，它并没有解释为什么这些组件都存在。如果你仔细研究这些数据，你看到的是，在12个月的周期的最低值往往在二月份出现，而最大值出现在七月。这些数据似乎合理的解释是，人们自然更活跃在夏季比冬季。不幸的是，因为这增加了活动的结果，有致命事故的发生概率提高。

参考

Brockwell，彼得J.，和理查德·戴维斯。时间序列：理论与方法。纽约：施普林格，2006年。

沙姆韦，罗伯特H.，和David S.斯托弗。时间序列分析及其为R应用实例。纽约：施普林格，2006年。

也可以看看

FFT|IFFT|xcorr