拉普拉斯操作员的特征值

打开直播脚本

这个例子说明了如何解决l形区域上拉普拉斯算子的特征值问题。

膜的问题

考虑固定在边界处的膜。 $\partial Ω$ 一个地区 $Ω$ 在飞机上。它的位移 $U (x, Y)$ 由特征值问题描述 $Δ U = λ U$ ,在那里 $Δ U = U_{x x} + U_{Y Y}$ 是拉普拉斯算子和 $λ$ 为标量参数。边界条件为 $U (x, Y) = 0$ 对所有 $(x, Y) \in \partial Ω$ .

拉普拉斯算子是自伴负定的，即只有实负特征值 $λ$ 存在有一个最大（负）离散特征值，对应的特征函数 $U$ 被称为基态.在本例中， $Ω$ 是一个l型区域，与此区域相关联的基态是MATLAB®标志的l型膜。

九点有限差分近似

解决特征值问题的最简单的方法是近似拉普拉斯算子 $Δ U$ 通过有限差分近似（a钢网)在具有距离的点的正方形网格上hx在里面 $x$ 方向和距离hy在里面 $Y$ 方向。在本例中，近似 $Δ U$ 用一笔S_h由围绕中点的九个规则网格点组成 $(x, Y)$ .未知数就是重量 ${A.}_{- 1. - 1.}, \dots, {A.}_{1. 1.}$ .

信谊u (x, y)EPSA11A10a1_1A01A00a0_1a_11a_10a_1_1信谊hxhy积极的s_h = a_11 * u（x  -  eps * hx，y + eps * hy）+......(1) x (x,y + y......(a) x + e *h,y + e *h,y + e *h......(x - Eps*hx,y) +......* u(x,y) +......A10 * U（X + EPS * HX，Y）+......a_1_1* u(x - Eps*hx,y - Eps*hy) +......1 . u(x,y - y) + (x,y......(x + y *h,y - y);

使用符号参数EPS通过权力对此表达的扩展进行分类hx和hy. 知道权重后，可以通过设置EPS = 1.

T =泰勒（S_H，EPS，'命令'7);

使用非零系数函数以提取具有相同项幂的项的系数EPS.每个系数都是一个表达式，包含hx,hy，以及U关于 $x$ 和 $Y$ . 自从S_h代表 $U_{x x} + U_{Y Y}$ ，的所有其他导数的系数U必须是零。通过替换所有的导数来提取系数U除了 $U_{x x}$ 和 $U_{Y Y}$ ，以0。代替 $U_{x x}$ 和 $U_{Y Y}$ 到1点。这将泰勒展开减少到您想要计算的系数，并导致以下六个线性方程。

C =公式(coeffs(t, Eps，“全部”));方程= subs(C(7)，u(x,y)) == 0;eq11 =潜艇(C (6), (diff (u, x) diff (u, y)], [1,0]) = = 0;eq12 =潜艇(C (6), (diff (u, x) diff (u, y)], [0,1]) = = 0;eq21 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [1, 0, 0)) = = 1;eq22 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [0, 1,0]) = = 0;eq23 =潜艇(C (5), (diff (u, x, x) diff (u, x, y), diff (u, y, y)], [0, 0, 1]) = = 1;

由于有九个未知权重S_h，通过要求U是0。

eq31 = summ（c（4），[diff（u，x，x，x），diff（u，x，x，y），diff（u，x，y，y），diff（u，y，y，Y），[1,0,0,0]）== 0;eq32 = summ（c（4），[diff（u，x，x，x），diff（u，x，x，y），diff（u，x，y，y），diff（u，y，y，y）]，[0,1,0,0]）== 0;eq33 = summ（c（4），[diff（u，x，x，x），diff（u，x，x，y），diff（u，x，y，y），diff（u，y，y，y）]，[0,0,1,0]）== 0;eq34 = summ（c（4），[diff（u，x，x，x），diff（u，x，x，y），diff（u，x，y，y），diff（u，y，y，y），[0,0,0,1]）== 0;

解决九个未知权重的由此产生的十个方程。用returnconditions.找到包括任意参数在内的所金宝搏官方网站有解。

[A11，A10，A1_1，A01，A00，A0_1，A_11，A_10，A_1_1，参数，条件] =......解决（[EQ0，EQ11，EQ12，EQ21，EQ22，EQ23，EQ31，EQ32，EQ33，EQ34，EQ34]，......[A11，A10，A1_1，A01，A00，A0_1，A_11，A_10，A_1_1]，......“ReturnConditions”，真的）;展开（[A_11，A01，A11;......a_10、a00 a01;......a1_1、a0_1 a_1_1])

ans=
                 
                   $(\begin{array}{c} Z & \frac{1.}{{hy}^{2.}} - 2. Z & Z \\ \frac{1.}{{hx}^{2.}} - 2. Z & 4. Z - \frac{2.}{{hx}^{2.}} - \frac{2.}{{hy}^{2.}} & \frac{1.}{{hy}^{2.}} - 2. Z \\ Z & \frac{1.}{{hy}^{2.}} - 2. Z & Z \end{array})$

参数

参数=
                  $Z$

使用subs函数以将权重替换为其计算值。

C =简化(潜艇(C));

的表情C（7）,C（6），和C（4）包含第0个、第1个和第3个U消失

[C（7），C（6），C（4）]

ans=
                  $(\begin{array}{c} 0 & 0 & 0 \end{array})$

表达方式C（5）是拉普拉斯式的U.

C（5）

ans=
                 
                   $\frac{\partial^{2.}}{\partial x^{2.}} U (x, Y) + \frac{\partial^{2.}}{\partial Y^{2.}} U (x, Y)$

因此，通过上面计算的权重值，模具S_h将拉普拉斯近似到最高阶hx^2,hy^2对于任意参数的任何值Z，条件是Z被选为有秩序的O (1 / hx ^ 2, 1 / hy ^ 2).

含有第四和高阶衍生物的条款

尽管解包含一个自由参数Z，表示C（3）包含四阶衍生物U不能由一个合适的选择变成零Z.另一种选择是将其转换为Laplace操作员的正方形。

信谊D拉普拉斯=@（u）拉普拉斯（u，[x，y]）；展开（d*拉普拉斯（拉普拉斯（u）））

ans (x, y) =
                 
                   $D \frac{\partial^{4.}}{\partial x^{4.}} U (x, Y) + 2. D \frac{\partial^{2.}}{\partial Y^{2.}} \frac{\partial^{2.}}{\partial x^{2.}} U (x, Y) + D \frac{\partial^{4.}}{\partial Y^{4.}} U (x, Y)$

挑选不同的衍生品U在里面C（3），并将其系数与相应的项相等。

subs（C（3），[diff（u，x，x，x，x），diff（u，x，x，y，y），diff（u，y，y，y）]，[1,0,0]）==d

ans=
                 
                   $\frac{{hx}^{2.}}{12.} = D$

子（C（3），[差异（u，x，x，x，x），diff（u，x，x，y，y），diff（u，y，y，y，y）]，[0，1,0]）== 2 * d

ans=
                  ${hx}^{2.} {hy}^{2.} Z = 2. D$

潜艇(C (3), [diff (u, x, x, x, x), diff (u, x, x, y, y), diff (u, y, y, y, y)], [0, 0, 1]) = = d

ans=
                 
                   $\frac{{hy}^{2.}}{12.} = D$

因此，你可以选择D = hx^2/12 = hy^2/12和z=2*d/（hx^2*hy^2），暗示hx=hy和Z = 1 /（6 * HX * HY）.因此，模版S_h在方形网格上近似改进的拉普拉斯hx = hy = h.

$s_{H} = Δ U + \frac{H^{2.}}{1. 2.} Δ^{2.} U + O (H^{3.}) . (1.)$

信谊Hhx=h；hy=h；d=h^2/12；

取代hx和hy通过H.

C =潜艇(C);

取代Z通过其价值，h ^ 1 / (6 * 2).因为ZMATLAB®工作区中不存在，您只能以存储在参数大堆

C =潜艇(C、参数1 / (6 * h ^ 2));

验证公式(1)。

简化(C (3) - d *拉普拉斯(拉普拉斯(u)))

ans (x, y) =
                  $0$

现在，考虑三阶项hx,hy.

简化（C（2））

ans=
                  $0$

由于在模板的扩展中没有存在这些条款，因此术语 $O (H^{3.})$ 在（1）中，事实上是有序的 $O (H^{4.})$ . 考虑模版的四阶项。

系数（简化（C（1）））

ans=
                 
                   $(\begin{array}{c} \frac{1.}{360.} & H & H & H & H & \frac{\partial^{6.}}{\partial x^{6.}} U (x, Y) + 5. \frac{\partial^{2.}}{\partial Y^{2.}} \frac{\partial^{4.}}{\partial x^{4.}} U (x, Y) + 5. \frac{\partial^{4.}}{\partial Y^{4.}} \frac{\partial^{2.}}{\partial x^{2.}} U (x, Y) + \frac{\partial^{6.}}{\partial Y^{6.}} U (x, Y) \end{array})$

检查这些术语是否可以用LaPlace运算符的另一个电源识别。但是，比较

拉普拉斯（拉普拉斯（拉普拉斯（u）））

ans (x, y) =
                 
                   $\frac{\partial^{6.}}{\partial x^{6.}} U (x, Y) + 3. \frac{\partial^{2.}}{\partial Y^{2.}} \frac{\partial^{4.}}{\partial x^{4.}} U (x, Y) + 3. \frac{\partial^{4.}}{\partial Y^{4.}} \frac{\partial^{2.}}{\partial x^{2.}} U (x, Y) + \frac{\partial^{6.}}{\partial Y^{6.}} U (x, Y)$

说明了表达式的顺序 $O (H^{4.})$ 不能被识别为拉普拉斯算子的三次方的倍数，因为系数不能匹配。

总结

对于有距离的正方形网格H在相邻栅格点和上述权重选择之间，可以得到：

$s_{H} = Δ U + \frac{H^{2.}}{1. 2.} Δ^{2.} U + O (H^{4.}) . (2.)$

用这个展开式求解特征值问题的数值方法 $Δ U = λ U$ . 加上几倍 $Δ^{2.} U = λ^{2.} U$ 到特征值方程。

$Δ U + \frac{H^{2.}}{1. 2.} Δ^{2.} U = (λ + \frac{H^{2.}}{1. 2.} λ^{2.}) U .$

该等式的左侧由模板很好地逼近 $s_{H}$ . 因此，使用（2），数值特征值 $μ$ 模板的质量令人满意 $s_{H} U = μ U$ 必须是特征值的近似值 $λ$ 拉普拉斯运营商的

$μ = λ + \frac{H^{2.}}{1. 2.} λ^{2.} + O (H^{4.}) .$

理所当然 $μ$ ,解决 $λ$ 得到拉普拉斯特征值的一个更好的近似。注意，在二次方程的解中 $λ$ 方形的正确迹象是由要求提供的 $λ \to μ$ 对于 $H \to 0$ .

$λ = \frac{6.}{H^{2.}} (\sqrt{1. + \frac{μ H^{2.}}{3.}} - 1.) = \frac{2. μ}{\sqrt{1. + \frac{μ H^{2.}}{3.}} + 1.} . (3.)$

用符号矩阵求解特征值问题

考虑L形区域 $Ω$ 由三个单位正方形组成。

$Ω = {(x, Y); - 1. \leq. x \leq. 0, - 1. \leq. Y \leq. 0} \cup {(x, Y); 0 \leq. x \leq. 1., - 1. \leq. Y \leq. 0} \cup {(x, Y); - 1. \leq. x \leq. 0, 0 \leq. Y \leq. 1.} .$

定义区域角点的坐标值。

xmin = 1;xmax = 1;ymin = 1;Ymax = 1;

考虑由奇数组成的正方形网格nx = 2 * nx-1网格点x方向和奇数ny = 2 * ny-1网格点Y方向。

nx=6；Nx=2*Nx-1；hx=（xmax xmin）/（Nx-1）；ny=6；Ny=2*Ny-1；hy=（ymax-ymin）/（Ny-1）；

创建一个纽约——- - - - - -NX.象征性的矩阵 $U$ . 它的条目u (i, j)代表的值U (xmin + (j - 1)*hx,ymin + (i - 1)*hy)解决方案的u (x, y)特征值问题 $Δ U = λ U$ .

u =符号(“你”，[Ny，Nx]）；

边界 $Ω$ 对应以下索引：

左边界对应于（i=1:Ny，j=1）.
下界对应于（i = 1，j = 1：nx）.
正确的边界对应于（i=1:ny，j=Nx）和（i=ny:ny，j=nx）.
上边界对应于（i = ny，j = 1：nx）和（i=ny，j=nx:nx）.

U（：，1）= 0;%左边界u（1，：）=0；%下边界U（1：NY，NX）= 0;%右边界，上部u（ny:ny，nx）=0；%右边界，下半部分u (Ny, 1: nx) = 0;%上边界，左边部分nx u(纽约:nx) = 0;%上边界，右部分

有 $0 < x \leq. 1.$ 和 $0 < Y \leq. 1.$ 不属于 $Ω$ . 设置相应的矩阵项(i = ny + 1: ny, j = nx + 1: nx)为零。它们不再扮演任何角色，也将被忽视。

u（ny+1:ny，nx+1:nx）=0；

问题的未知是以下矩阵条目：

u =
                 
                   $(\begin{array}{c} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & U_{2., 2.} & U_{2., 3.} & U_{2., 4.} & U_{2., 5.} & U_{2., 6.} & U_{2., 7.} & U_{2., 8.} & U_{2., 9} & U_{2., 10.} & 0 \\ 0 & U_{3., 2.} & U_{3., 3.} & U_{3., 4.} & U_{3., 5.} & U_{3., 6.} & U_{3., 7.} & U_{3., 8.} & U_{3., 9} & U_{3., 10.} & 0 \\ 0 & U_{4., 2.} & U_{4., 3.} & U_{4., 4.} & U_{4., 5.} & U_{4., 6.} & U_{4., 7.} & U_{4., 8.} & U_{4., 9} & U_{4., 10.} & 0 \\ 0 & U_{5., 2.} & U_{5., 3.} & U_{5., 4.} & U_{5., 5.} & U_{5., 6.} & U_{5., 7.} & U_{5., 8.} & U_{5., 9} & U_{5., 10.} & 0 \\ 0 & U_{6., 2.} & U_{6., 3.} & U_{6., 4.} & U_{6., 5.} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & U_{7., 2.} & U_{7., 3.} & U_{7., 4.} & U_{7., 5.} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & U_{8., 2.} & U_{8., 3.} & U_{8., 4.} & U_{8., 5.} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & U_{9, 2.} & U_{9, 3.} & U_{9, 4.} & U_{9, 5.} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & U_{10., 2.} & U_{10., 3.} & U_{10., 4.} & U_{10., 5.} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array})$

区域的内部点

Ω ∖ \partial Ω

与指数相对应

(我, J)

包含未知值的

U (我, J)

问题。在向量中收集这些未知数vars..

将符号表达式与每个索引（即每个未知）相关联（由本示例的第一部分中导出的模板给出）。

因为这个表达式在未知元素中是线性的U(存储在vars.)，你可以把它看作作用于向量的矩阵vars..

你可以治疗S_h作为拉普拉斯算子的矩阵近似。计算其特征向量和特征值。

因为对于这个近似，你使用了一个有少量点的网格，只有特征值的前导数字是正确的。

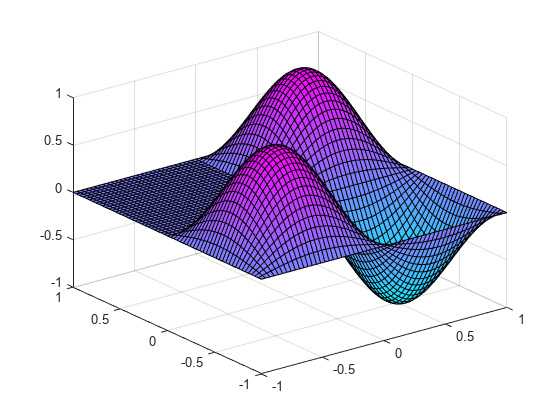
L形区域上拉普拉斯算子的第三高特征值

Ω

这是众所周知的。拉普拉斯算子的精确本征函数是

U (x, Y) = 罪 (π x) 罪 (π Y)

与(确切的)特征值相关联的

- 2. π^{2.} = - 1. 9 . 7. 3. 9 2. . . .

. 实际上，使用上面的方程（3），你可以得到拉普拉斯特征值的更好的近似值

λ

从模板特征值

μ

使用双精度矩阵来解决特征值问题

当您使用符号矩阵时，不建议毫无推荐地增加网格点数，因为符号计算比使用MATLAB双精度矩阵的数值计算显着慢。该示例的这一部分演示了如何使用稀疏双算法，允许改进数值网格。L形区域

Ω

与以前相同的方式设置。通过符号未知数，而不是表示内部点，而是初始化网格值U并定义

Ω

通过将边界点和外部点的值设置为零。而不是定义每个内部点的符号表达，而是将模板计算为jacobian，直接将模板矩阵直接设置为稀疏矩阵。

这里，S_h是（稀疏）模具矩阵。使用EIG它处理稀疏矩阵来计算三个最大的特征值。

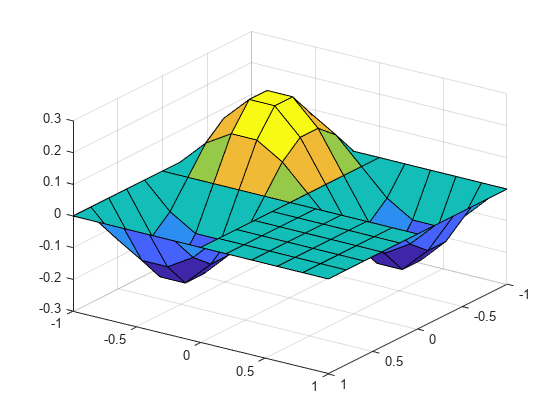
D（3,3）近似准确的特征值

- 2. π^{2.} = - 1. 9 . 7. 3. 9 2. 0 8. 8. . . .

.使用上述方程式（3），推导拉普拉斯特征值的更精确近似值

λ

从模板特征值

μ

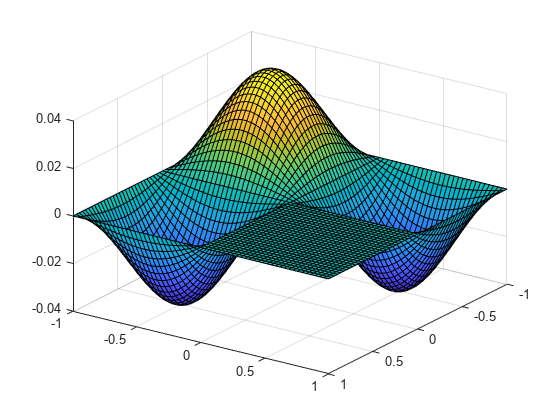
注意，MATLAB膜函数通过不同的方法计算拉普拉斯算子的本征函数。

拉普拉斯操作员的特征值

膜的问题

九点有限差分近似

含有第四和高阶衍生物的条款

总结

用符号矩阵求解特征值问题

使用双精度矩阵来解决特征值问题

符号数学工具箱文档

金宝app

数学建模与符号数学工具箱