非抽取离散平稳小波变换(SWTs) - MATLAB和Simulink金宝app - 金宝app,下载188bet金宝搏,金宝搏官方网站

非抽取离散平稳小波变换

我们知道经典的小波变换有一个缺点:小波变换不是定常变换。这意味着，即使是周期信号扩展，信号翻译后的DWTX是不是，一般来说，DWT的翻译版本X．

如何恢复平移不变性，这是经典DWT所丢失的一个理想性质?其思想是对一些略有不同的小波变换(ε-decimated DWT)进行平均，以定义平稳小波变换(SWT)。此属性对于多个应用程序(如断点检测)非常有用。

SWT的主要应用是去噪。有关基本原理的更多信息，请参阅[CoiD95]参考文献．有关示例,请参见一维平稳小波变换和二维平稳小波变换．

其原理是对几个去噪信号进行平均。它们中的每一个都是使用通常的去噪方案(见小波去噪与非参数函数估计)，但适用于ε-decimated DWT的系数。

请注意

SWT仅对长度可被2整除的信号定义^J,在那里J为最大分解级别。SWT使用周期性(每)扩展。

ε摧毁DWT

什么是ε-decimated DWT?

离散小波变换有很多不同的处理方法。让我们回想一下，DWT的基本计算步骤是卷积后进行抽取。抽取甚至保留了索引元素。

但抽取可以通过选择奇数索引元素而不是偶数索引元素来实现。这个选择涉及到分解过程的每一步，所以在每一层我们都选择奇数或偶数。

如果我们对原始信号进行所有可能的分解，得到2^J不同的分解，对于给定的最高水平J．

让我们用ε表示_j= 1或0在step中选择奇数或偶数索引的元素j．每个分解都用0和1的序列标记:ε = ε₁…,ε_J．这种变换称为ε-decimated DWT。

通过对标准DWT的基向量进行移位，可以得到ε-decimated DWT的基向量，并对应于基函数原点的特殊选择。

如何计算ε-Decimated DWT: SWT

通过计算每个可能序列ε的近似和细节系数，可以计算出长度为N的给定信号的所有ε-decimated DWT。通过迭代来完成，表单DWT的基本步骤的一个稍微修改的版本:

[D] = dwt (X, wname‘模式’,‘/’,‘转移’,e);

最后两个参数指定执行抽取步骤的方式。这是经典的e =0,但是对于e =奇数索引的元素通过抽取保留下来。

当然，这不是计算所有ε-decimated DWT的好方法，因为许多计算要执行很多次。现在我们将描述另一种方法，即平稳小波变换(SWT)。

SWT算法非常简单，接近DWT算法。更准确地说，对于第1级，一个给定信号的所有ε-抽取小波分量(在这个级别只有两个)，可以像小波分量的情况下一样，通过与适当的滤波器卷积得到，但不需要下采样。然后，第1级的近似系数和细节系数都是大小的N，即信号长度。这可以在下图中显示出来。

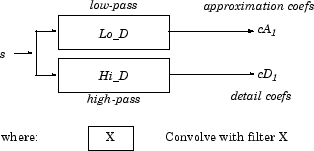
一般的步骤j在水平处卷积近似系数j-1，使用适当的原始滤波器的上采样版本，以产生水平上的近似和细节系数j．这可以在下图中显示出来。

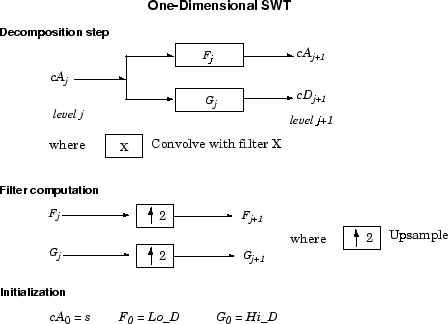
接下来，我们演示了如何从SWT的近似和细节系数结构中提取给定的ε-decimated DWT。

我们用SWT分解高度序列，在级别上J= 3，使用正交小波。

这个函数swt依次计算下列数组，其中一个(j,ε₁,…,ε_j）或D (j,ε₁,…,ε_j）表示水平上的近似或细节系数jε=[ε]， ε-decimated DWT₁,…,εj]．

步骤0(原始数据)

一个(0)

步骤1

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
(1,0)	(1)	(1,0)	(1)	(1,0)	(1)	(1,0)	(1)

步骤2

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
D (2 0 0)	D (2, 1, 0)	D (2 0 1)	D (2, 1, 1)	D (2 0 0)	D (2, 1, 0)	D (2 0 1)	D (2, 1, 1)
(2, 0, 0)	(2, 1, 0)	(2 0 1)	(2, 1, 1)	(2, 0, 0)	(2, 1, 0)	(2 0 1)	(2, 1, 1)

步骤3

D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)	D (1,0)	D (1,1)
D (2 0 0)	D (2, 1, 0)	D (2 0 1)	D (2, 1, 1)	D (2 0 0)	D (2, 1, 0)	D (2 0 1)	D (2, 1, 1)
D (0, 0, 0)	D(3、1,0,0)	D (3 0 1 0)	D (3 1 1 0)	D (0, 0, 1)	D (3, 1,0, - 1)	D (0, 1, 1)	D(3、1、1、1)
(3, 0, 0, 0)	(3、1 0 0)	(3 0 1 0)	(3 1 1 0)	(3 0 0,1)	(3, 1,0, - 1)	(3 0, 1, 1)	(3、1、1、1)

让j表示当前电平，其中j也是算法的当前步骤。然后我们得到ε的抽象关系_我= 0或1:

[tmpAPP, tmpDET] = dwt ((j,ε₁,ɛ_j)、wname‘模式’,‘/’,‘转移’,ɛ_{j + 1}）;一个(j + 1,ɛ₁,ɛ_j,ɛ_{j + 1}) = circshift (tmpAPP,ɛ_{j + 1}）;D (j + 1,ɛ₁,ɛ_j,ɛ_{j + 1}) = circshift (tmpDET,ɛ_{j + 1}）;

在哪里circshift对输入向量进行ε-圆位移。因此,如果ε_j＋１= 0,circshift指令是无效的，可以被压制。

设ε = [ε .₁,…,ε_J与ε)_我= 0或1。我们有2^J= 2^3.= 8个不同的3级ε-decimated dwt。选择ε，我们可以从SWT阵列中得到相应的ε-decimated DWT。

现在，考虑最后一步，J= 3，设[Cε，Lε]表示ε-decimated DWT对给定ε的小波分解结构。然后，通过选择合适的系数从SWT分解结构中检索，如下所示:

Cε=

(3ε₁,ε₂,ε_3.）

D(3ε₁,ε₂,ε_3.）

D(2ε₁,ε₂）

D(ε₁）

Lε= [1,1,2,4,8)

例如ε-decimated DWT对应于ε = [ε₁,ε₂,ε_3.=[1,0,1]在前面示例的数组序列中以粗体显示。

这可以扩展到二维情况。图像平稳小波变换的算法如下图所示。

逆离散平稳小波变换(ISWT)

每个ε-decimated DWT对应于一个给定的ε可以被反演。

利用给定的ε-decimated小波变换(ε-decimated DWT)重构原始信号₁,…,ε_J，我们可以使用抽象算法

FOR j = j:-1:1 A(j-1， ε₁,ɛ_{j - 1}) =…得到一个(ɛj₁,ɛ_j)、D (S,ɛ₁,ɛ_jwname)],“模式”,“每”、“转变”,ɛ_j）;结束

对于每个ε = (ε₁,…,ε_J)，我们得到原始信号A(0)，从略有不同的分解开始，以不同的方式捕捉分析信号的主要特征。

离散平稳小波逆变换的思想是对每一个ε-decimated小波变换的逆变换求平均。这可以从级别开始递归地完成J到第一级。

ISWT通过以下抽象算法得到:

FOR j = j:-1:1 X0 = idwt(A(j，ɛ.)₁,ɛ_jɛ)、D (j₁,ɛ_j), wname,…“模式”、“每”、“转变”,0);X1 =得到((ɛj₁,ɛ_jɛ)、D (j₁,ɛ_j), wname,…“模式”、“每”、“转变”,1);X1 = circshift (X1, 1);(ɛj - 1₁,ɛ_{j - 1}) = (X0 + X1) / 2;结束

沿着同样的思路，这可以扩展到二维情况。