建模框架概述

本例的最终目的是比较来自不同噪声过程的一篮子期权价格。第一个噪声过程是一个传统的布朗运动模型，其指数组合价格过程是由相关高斯随机吸引驱动的。另一种方法是将布朗运动基准与高斯和学生驱动的噪声过程进行比较t交媾，统称为a布朗系词。

copula是一个边缘分布均匀的多元累积分布函数(CDF)。虽然理论基础是几十年前建立的，但在过去几年里，copulas经历了一次巨大的流行，主要是作为一种建模非高斯投资组合风险的技术。

虽然存在大量的科系，但所有的交点都代表了一种统计工具，用于模拟两个或多个随机变量之间的依赖结构。此外，重要的统计数据，如等级相关和尾巴的依赖是一个给定的系词的性质和不变通过他们的利润的单调变换。

这些连接词产生相关的随机变量，这些随机变量随后被转换成单独的变量(边距)。这种转换是通过具有广义帕累托尾的半参数概率分布实现的。

要模拟的风险中性市场模型是

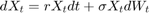
其中无风险利率，r，是在期权的有效期假设为常数。因为这是一个可分离的多变量模型，无风险回报率是在相同的无风险回报率适用于所有指数对角矩阵。股息收益率都将被忽略，以简化模型及其相关数据的收集。

相比之下，曝光矩阵的规格，σ，取决于不确定性的驱动源是如何建模的。你可以直接将它建模为一个布朗运动(相关高斯随机数隐式映射到高斯边缘)，或者将它建模为一个布朗copula(相关高斯或t随机数字显式映射到半参数边值)。

由于单变量分布的CDF和逆CDF(分位数函数)都是单调变换，因此copula提供了一种方便的方法来模拟边缘不相似且任意分布的相依随机变量。此外，由于copula定义了一个给定的依赖结构，而不考虑它的边界，copula参数校准通常比联合分布函数的估计更容易。

一旦你的模拟样本路径，选择由朗斯塔夫＆施瓦茨（见的最小二乘回归方法定价通过模拟美国价值评估选项：一个简单的最小二乘法，《金融研究评论》，2001年春季)。这种方法使用最小二乘法来估计如果不立即执行期权的预期收益。它是通过将未来收到的贴现期权现金流回归到与所有货币样本路径相关的底价的当前价格上来实现的。延拓函数由一个简单的三阶多项式估计，其中回归中的所有现金流和价格都用期权执行价格标准化，提高了数值稳定性。

导入支持的历史数据集金宝app

加载一个3个月Euribor的每日历史数据集，交易日期从07-Feb-2001到24-Apr-2006，以及以下代表性大型股票指数的收盘指数水平:

清晰的负载Data_GlobalIdx2

下面的图说明了这些数据。具体而言，这些图表显示了各指数的相对价格走势和欧元区银行间同业拆借利率(Euribor)的无风险利率代理。每个指标的初始水平已标准化为统一，以便比较历史记录的相对性能。

nIndices =大小(数据,2)1;索引的% #价格=数据（：，1：端-1）;产率=数据（：，端）;日有效产量%收率= 360 *日志（1 +产率）;连续复合年化产率情节(日期、ret2tick (tick2ret(价格,“方法”,“连续”）“方法”,“连续”））datetick（“x”）xlabel（“日期”）ylabel（“指数值”)标题(“正常每日指数收盘”）图例（系列{1：端-1}，'位置',“西北”)

plot(日期，100 *产量)“x”）xlabel（“日期”）ylabel（'年收益率（％）')标题(“无风险利率（3个月期Euribor连续复合的）”)

极值理论和分段概率分布

为了准备copula模型，分别描述每个指数的收益分布。虽然每个回归序列的分布可以用参数化的方法来描述，但是使用具有广义帕累托尾的分段分布来拟合半参数模型是有用的。它使用极值理论来更好地描述每个尾部的行为。

统计和机器学习工具箱™软件目前支持两种与EVT相关的单变量概率分布，EVT是一种用于建模金融数据(如资产回报和保险损失)厚尾行为金宝app的统计工具:

下面的分析强调了在风险管理应用程序中更广泛使用的Pareto分布。

假设我们要创建的股票指数中的任一项日常资产收益的概率分布的一个完整的统计描述。假设该描述是通过一个分段半参数分布，其中在每个尾部的渐近行为的特征在于广义Pareto分布提供。

最终，一个copula将被用来产生随机数来驱动模拟。CDF和逆CDF转换将捕获模拟收益的波动性，作为SDE的扩散项的一部分。各指标的平均收益率由无风险利率控制，并纳入SDE的漂移项。下面的代码段集中了每个索引的返回(即提取平均值)。

由于下面的分析使用了极值理论来描述每个股票指数回报序列的分布，因此有助于研究特定国家的细节:

返回= tick2ret(价格,“方法”,“连续”);将价格转换为收益返回= bsxfun(@减，返回，均值(返回));％中心的回报指数= 3;%德国存储在第3列情节（日期（2：结束），返回（：，索引））datetick（“x”）xlabel（“日期”）ylabel（'返回'）标题（[“每日对数收益为中心：”系列{指数}])

请注意，此代码段可以更改为检查任何国家的详细信息。

使用这些中心的回报，估计每个索引的经验，或非参数，CDF具有高斯内核。这种平滑CDF估计，消除非平滑样本的CDF的阶梯模式。虽然非参数内核CDF估计非常适合的分布，其中大部分的数据被发现的内部，他们往往在施加到上和下尾表现不佳。为了更好地估计分布的尾部，适用于EVT落在每个尾部的回报。

具体地说，找到最高和最低的阈值，以便为每个尾部保留10%的回报。然后根据极大似然法，拟合每个尾部的极端收益超过相关阈值到帕累托分布的数量。

下面的代码段创建了一个类型对象paretotails对于每个索引返回序列。这些Pareto尾对象封装了参数化Pareto下尾、非参数化核平滑内部和参数化Pareto上尾的估计，从而为每个指标构建一个复合半参数化CDF。

tailFraction = 0.1;％小数分配给每个尾尾巴=细胞(nIndices, 1);帕累托尾对象％单元阵列为I = 1：nIndices尾巴{I} = paretotails（返回（：，i）中，tailFraction，1  -  tailFraction，'核心');结束

得到的分段分布对象允许在CDF内部插值和在每个尾部外推(功能评估)。外推法允许对历史记录之外的分位数进行估计，这对于风险管理应用程序是非常宝贵的。

帕累托尾对象也提供方法评估CDF和逆CDF（位数功能），以及查询所述分段分布的每个段之间的边界的累积概率和位数。

现在已经估计了分段分布的三个不同区域，以图形方式连接和显示结果。

下面的代码调用了感兴趣的Pareto tails对象的CDF和逆CDF方法，所使用的数据与fit所基于的数据不同。引用的方法可以访问拟合状态。它们现在被用来选择和分析概率曲线的特定区域，作为一个强大的数据过滤机制。

作为参考，图还包括相同的标准偏差的零均值高斯CDF。到一定程度，在期权价格的变化反映在何种程度上每个资产不同的从该正常曲线分布。

minProbability = CDF（尾部{索引}，（分钟（返回（：，索引））））;maxProbability = CDF（尾部{索引}，（最大（返回（：，索引））））;pLowerTail = linspace（minProbability，tailFraction，200）;％下尾pUpperTail = linspace（1  -  tailFraction，maxProbability，200）;％上尾pinner = linspace(尾分数，1 -尾分数，200);%的室内情节(icdf(反面{指数},pLowerTail) pLowerTail,“红色”,“线宽”2）保持上格上情节（ICDF（尾部{索引}，pInterior），pInterior，“黑”,“线宽”， 2) plot(icdf(tails{index}， pUpperTail)， pUpperTail，“蓝”,“线宽”极限=轴;x = linspace(极限(1)，极限(2));plot(x, normcdf(x, 0, std(returns(:，index))))，'绿色',“线宽”， 2)图= gcf;fig.颜色= [1,1,1];持有离xlabel（“集中返回”）ylabel（'可能性')标题(“半参数/分段CDF：”传奇系列{指数}])({“帕累托低尾”内核内部平滑的…“帕累托上尾”'Gaussian with Same \sigma'},'位置',“西北”)

下部和上部尾部区域，在红色和蓝色显示，分别适合于外插，而内核平滑内部，在黑色，是适合于内插。

连系动词校准

统计和机器学习工具箱软件包括的功能，校准和模拟高斯和t连系动词。

利用每天的指数收益，估计高斯的参数和t使用功能连接函数copulafit。自t当标量自由度参数(DoF)变得无限大时，这两个copula实际上是同一科的，因此共享一个作为基本参数的线性相关矩阵。

虽然高斯系词的线性相关矩阵的校准很简单，一个的校准t系词是没有的。为此，统计和机器学习Toolbox软件提供了两种技术来校准t连系动词:

当均匀变量被每个边缘的经验CDF转换时，这种校准方法通常被称为正则极大似然(CML)。下面的代码段首先通过上面推导的分段半参数CDFs将以日为中心的返回值转换为一致的变量。然后它符合高斯分布t转换后的数据交点:

U = 0(大小(回报));为i = 1: nIndices U (:, i) = cdf(反面{我},返回(:,我));将每个边距转换为均匀的结束选项= statset（'显示',“关”,“TolX”1的军医);[rhoT, DoF] = copulafit(“t”U“方法”,“ApproximateML”,“选项”、选择);rhoG = copulafit (“高斯”U);

所估计的相关矩阵是非常相似但不相同。

corrcoef（返回）日收益的线性相关矩阵

ans = 1.0000 0.4813 0.5058 0.6526 0.4813 1.0000 0.8485 0.2261 0.4617 1.0000 0.2001 0.7650 0.6136 0.2261 0.2001 0.2295 0.1473 0.4573 0.8575 0.2295 1.0000 0.4617 0.6526 0.5102 0.1439 0.4617 1.0000

rhoG%的线性相关矩阵的优化高斯copula

rhoG = 1.0000 0.4745 0.5018 0.1857 0.4721 0.6622 0.4745 1.0000 0.8606 0.2393 0.8459 0.4912 0.5018 0.8606 1.0000 0.2126 0.7608 0.5811 0.1857 0.2393 0.2126 1.0000 0.2396 0.1494 0.4721 0.8459 0.7608 0.2396 1.0000 0.4518 0.6622 0.4912 0.5811 0.1494 0.4518 1.0000

rhoT优化后t copula的线性相关矩阵%

rhoT = 1.0000 0.4671 0.4858 0.1907 0.4721 0.4671 1.0000 0.4739 0.4769 1.0000 0.2326 0.7723 0.5877 0.1907 0.2567 0.2326 1.0000 0.2539 0.1539 0.4734 0.8500 0.7723 1.0000 0.4769 0.6521 0.5122 0.1539 0.4769 1.0000

注意从所获得的相对低的自由度参数的tcopula校准，表明明显偏离了高斯分布的情况。

景深％标度的优化吨系词自由参数的

景深= 4.8613

介体模拟

在估算了联结参数后，利用该函数模拟联合相关的均匀变量copularnd。

然后，通过对帕累托尾的外推和光滑内插，对推导出的一致变量进行变换copularnd通过每个指数的逆CDF以日为中心返回。这些模拟的居中返回与从历史数据集获得的结果一致。假设收益在时间上是独立的，但在任何时间点上都具有由给定的联结关系所引起的相关性和秩相关。

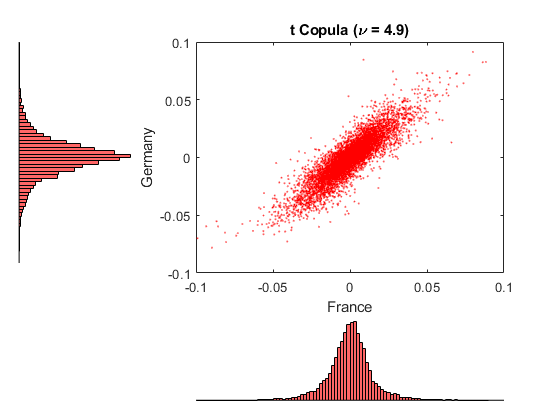
下面的代码段通过使用t连系动词。然后使用统计和机器学习工具箱为法国CAC 40和德国DAX绘制具有边缘直方图的二维散点图scatterhist功能。法国和德国的指标进行了简单的选择，因为他们有可用数据的相关性最高。

nPoints = 10000;模拟观测％＃s = RandStream.getGlobalStream ();重置(s) R = 0 (nPoints, nIndices);预分配模拟返回数组U = copularnd (“t”，RHOT，自由度，nPoints）;%从t copula中模拟U(0,1)为J = 1：nIndices R（：，J）= ICDF（尾部{Ĵ}，U（：，J））;结束h = scatterhist(R(:，2)， R(:，3)，'颜色',“r”,“标记”,“。”,'MarkerSize'1);无花果= gcf;fig.颜色= [1,1,1];日元= ylim (h (1));y3 = ylim (h (3));xlim (h (1), (-。1 .1]) ylim(h(1)，[-。1 .1]) xlim(h(2)，[-。1。1)ylim (h (3), ((y3 (1) + (-0.1 - y1 (1))) (y3 (2) + (0.1 - y1(2)))))包含(“法国”）ylabel（'德国'）标题（['t Copula (\nu = 'num2str(景深,2)'）']）

现在，模拟和情节使用高斯系词中心的回报。

重置(s) R = 0 (nPoints, nIndices);预分配模拟返回数组U = copularnd (“高斯”、rhoG nPoints);%从高斯copula中模拟U(0,1)为J = 1：nIndices R（：，J）= ICDF（尾部{Ĵ}，U（：，J））;结束h = scatterhist(R(:，2)， R(:，3)，'颜色',“r”,“标记”,“。”,'MarkerSize'1);无花果= gcf;fig.颜色= [1,1,1];日元= ylim (h (1));y3 = ylim (h (3));xlim (h (1), (-。1 .1]) ylim(h(1)，[-。1 .1]) xlim(h(2)，[-。1。1)ylim (h (3), ((y3 (1) + (-0.1 - y1 (1))) (y3 (2) + (0.1 - y1(2)))))包含(“法国”）ylabel（'德国')标题(“高斯系词”)

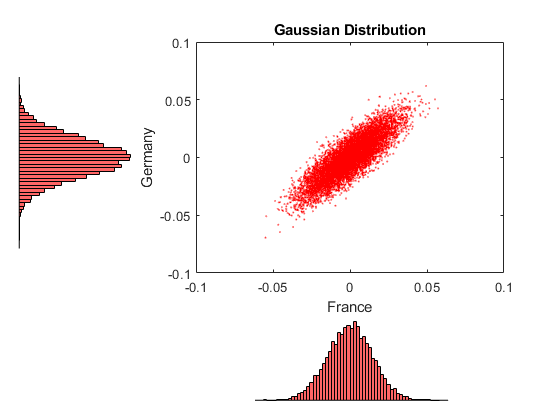
看看这两个数字。每个图形对应轴上的微型直方图之间有很强的相似性。这种相似性并非巧合。

这两个copula都模拟均匀随机变量，然后通过每个指数的分段分布的逆CDF将其转换为以日为中心的收益率。因此，任何给定索引的模拟返回值都是同分布的，而不受copula的影响。

然而，每个图的散点图表示与给定的连接函数相关联的相关结构，并且在与在所述直方图中所示的单变量边距，散点图是不同的。

再次，Copula函数定义的依赖结构，无论其利润率，并因此提供了许多功能单独不限于校准。

作为参考，使用传统的布朗运动模型下的高斯分布来模拟和绘制居中返回。

复位（S）R = mvnrnd（零（1，nIndices），COV（返回），nPoints）;h = scatterhist(R(:，2)， R(:，3)，'颜色',“r”,“标记”,“。”,'MarkerSize'1);无花果= gcf;fig.颜色= [1,1,1];日元= ylim (h (1));y3 = ylim (h (3));xlim (h (1), (-。1 .1]) ylim(h(1)，[-。1 .1]) xlim(h(2)，[-。1。1)ylim (h (3), ((y3 (1) + (-0.1 - y1 (1))) (y3 (2) + (0.1 - y1(2)))))包含(“法国”）ylabel（'德国')标题(高斯分布的)

采用Longstaff & Schwartz方法的美国期权定价

既然copula已经被校准了，那么比较一下从各种方法中得出的平价美国一揽子期权的价格。简单地分析一下，假设:

现在计算所有仿真方法共有的参数:

dt = 1 / 252;％时间增量= 1天=二百五十二分之一年产率=数据（：，端）;日有效产量%收率= 360 *日志（1 +产率）;％连续-复利，年收益率r =意味着(收益率);历史平均300万欧元X = repmat(100, nIndices, 1);％的初始状态矢量罢工= (X)之和;初始化一个取钱篮nTrials = 100;% #独立试验nPeriods = 63;仿真周期% #:63/252 = 0.25年= 3个月

现在，创建两个可分离多维市场的车型，其中无风险回报率和波动曝光矩阵都是对角线。

虽然两者都是对角GBM模型具有相同的风险中性返回时，第一是由相关的布朗运动驱动，并且明确指定样品线性中心返回的相关矩阵。此相关布朗运动过程然后通过年度指数波动率或标准偏差的对角矩阵加权。

另一种选择是，同样的模型可以由不相关的布朗运动驱动(标准布朗运动)通过指定相关作为单位矩阵，或者通过简单地接受默认值。在这种情况下，曝光矩阵σ指定为指标返回协方差矩阵的下Cholesky因子。由于基于copula的方法模拟相依随机数，为了一致性，选择了对角曝光形式。详情请见诱导依赖性和相关性的替代方案。

西格玛= STD（返回）* SQRT（252）;%的年化波动相关= corrcoef(回报);％相关高斯干扰GBM1 = gbm(diag(r(ones(1,nIndices)))， diag(sigma)，“StartState”,X,…“相关”、相关);

现在用单位矩阵建立第二个由布朗系数驱动的模型σ。

GBM2 = gbm(diag(r(one (nIndices)))， eye(nIndices)，“StartState”,X);

新创建的模型可能看起来不太寻常，但它突出了SDE体系结构的灵活性。

使用连系动词时,往往是方便让随机数生成器函数Z (t, X)诱导的依赖(线性相关的传统概念是一个特例)连系动词,并诱导变异的大小或规模(类似于波动或标准差)semi-parametric CDF和逆CDF实验组的转换。由于每个指数的CDF和逆CDF转换继承了历史回报率的特征，这也解释了为什么现在的回报率是居中的。

在下面的章节，之类的语句：

Z = Example_CopulaRNG（返回* SQRT（252），nPeriods， '高斯'）;

要么

z = Example_CopulaRNG(返回* sqrt(252)， nperiod， 't');

符合高斯和t分别是copula依赖结构，以及半参数边际到中心收益的比例为每年交易天数的平方根(252)。这种比例并没有对以日为中心的回报进行年化。相反，它使波动率与对角年化敞口矩阵保持一致σ之前建立的传统布朗运动模型(GBM1)。

在本例中，您还指定了一个期末处理函数，它接受状态(t,X)后的时间，并将投资组合的样本时间和值记录为所有指数的单单位加权平均值。该函数还与其他函数共享该信息，这些函数旨在使用Longstaff & Schwartz的最小二乘回归方法为具有恒定无风险利率的美国期权定价。

f = Example_LongstaffSchwartz(nperiod, nTrials)

f = struct with fields: longstaffprice: @Example_LongstaffSchwartz/ saveprices CallPrice: @Example_LongstaffSchwartz/getCallPrice PutPrice: @Example_LongstaffSchwartz/getPutPrice price: @Example_LongstaffSchwartz/getPutPrice

现在使用默认的模拟股票指数价格的独立试验超过3个日历月simByEuler方法。没有输出从模拟方法要求;实际上，各个索引的模拟价格包含篮子是不必要的。看涨期权价格为报道方便：

复位（S）simByEuler（GBM1，nPeriods，'nTrials'nTrials,“DeltaTime”，DT，…“流程”,f.LongstaffSchwartz);BrownianMotionCallPrice = f。CallPrice(罢工,r);BrownianMotionPutPrice = f。PutPrice(罢工,r);重置z = Example_CopulaRNG(返回* sqrt(252)， nperiod，“高斯”);f = Example_LongstaffSchwartz(nperiod, nTrials);simByEuler (GBM2 nPeriods,'nTrials'nTrials,“DeltaTime”，DT，…“流程”f.LongstaffSchwartz,'Z',z);GaussianCopulaCallPrice = f。CallPrice(罢工,r);GaussianCopulaPutPrice = f。PutPrice(罢工,r);

现在，随着重复系词模拟t连系动词结构的依赖。对两个交点使用相同的模型对象;只需要重新初始化随机数生成器和选项定价函数。

重置z = Example_CopulaRNG(返回* sqrt(252)， nperiod，“t”);f = Example_LongstaffSchwartz(nperiod, nTrials);simByEuler (GBM2 nPeriods,'nTrials'nTrials,“DeltaTime”，DT，…“流程”f.LongstaffSchwartz,'Z',z);tCopulaCallPrice = f.CallPrice（击，R）;tCopulaPutPrice = f.PutPrice（击，R）;

最后，比较来自所有模型得到的美式看跌和看涨期权的价格。

DISP（' '）fprintf中（'蒙特卡洛试验＃：％8D \ n'nTrials)流(时间段/试验的数量:%8d\n\n'，nPeriods）fprintf中（“布朗运动美国指数篮子价格:%8.4f\n”BrownianMotionCallPrice)流('布朗运动美式看跌篮子价格：％8.4f \ n \ n'，BrownianMotionPutPrice）fprintf中（' Gaussian Copula American Call Basket Price: %8.4f\n'GaussianCopulaCallPrice)流(' Gaussian Copula American Put Basket Price: %8.4f\n\n'GaussianCopulaPutPrice)流(美国存托股票篮子价格:%8.4f\n'tCopulaCallPrice)流(美国存托股票一篮子价格:%8.4f\n'tCopulaPutPrice)

蒙特卡洛试验＃：100＃时间段/试用：63的布朗运动的美式看涨篮子价格：25.9456布朗运动美式看跌篮子价格：16.4132高斯Copula函数的美式看涨篮子价格：24.5711高斯系词美式看跌篮子价格：17.4229吨系词美国呼叫篮子价格：22.6220吨Copula的美式看跌篮子价格：20.9983

此分析仅代表一个小规模的模拟。如果仿真重复10万次的试验，得到以下结果：

蒙特卡罗试验次数:100000次/试验次数:63次

布朗运动美国看跌篮子价格:20.2214布朗运动美国看跌篮子价格:16.5355

高斯系词美式看涨篮子价格：20.6097高斯系词美式看跌篮子价格：16.5539

牛逼系词美式看涨篮子价格：21.1273吨Copula的美式看跌篮子价格：16.6873

有趣的是，结果非常一致。从copulas获得的看跌期权价格比布朗运动的看跌期权价格高出不到1%。

关于波动性和利率调整的说明

同样的期权价格也可以通过（每天在这种情况下，）与unannualized工作中心的收益和无风险利率，其中时间增量获得dt=1天而非二百五十二分之一年。换句话说，投资组合的价格仍然会模拟每个交易日;数据被简单地缩放不同。

尽管没有执行，并且通过首先将随机流重置为其初始内部状态，下面的代码段使用以日为中心的回报率和无风险利率，并生成相同的期权价格。

高斯分布/布朗运动和日常数据：

复位（S）

f = Example_LongstaffSchwartz(nperiod, nTrials);GBM1 = gbm(diag(r(ones(1,nIndices))/252)， diag(std(returns))，“StartState”,X,…“相关”、相关);

simByEuler（GBM1，nPeriods，'nTrials'nTrials,“DeltaTime”,1…“流程”,f.LongstaffSchwartz);

BrownianMotionCallPrice = f。CallPrice(罢工，r/252) BrownianMotionPutPrice = f。PutPrice(罢工,r / 252)

高斯Copula &日数据:

复位（S）

z = Example_CopulaRNG(返回，nperiod，“高斯”);f = Example_LongstaffSchwartz(nperiod, nTrials);GBM2 = gbm(diag(r(ones(1,nIndices))/252)， eye(nIndices)，“StartState”,X);

simByEuler (GBM2 nPeriods,'nTrials'nTrials,“DeltaTime”,1…“流程”，f.LongstaffSchwartz，'Z',z);

GaussianCopulaCallPrice = f.CallPrice（击，R / 252）= GaussianCopulaPutPrice f.PutPrice（击，R / 252）

牛逼系词日用品数据：

复位（S）

z = Example_CopulaRNG(返回，nperiod，“t”);f = Example_LongstaffSchwartz(nperiod, nTrials);

simByEuler (GBM2 nPeriods,'nTrials'nTrials,“DeltaTime”,1…“流程”，f.LongstaffSchwartz，'Z',z);

tCopulaCallPrice = f.CallPrice（击，R / 252）= tCopulaPutPrice f.PutPrice（击，R / 252）