旋转,方向和四元数
这个例子回顾概念,三维旋转和四元如何被用来描述取向和旋转。四元数超复数的倾斜场。他们发现,在航空航天,计算机图形学和虚拟现实应用。在MATLAB®,四元数数学可以通过操纵来表示四元数班级。
这个HelperDrawRotation类用于说明此示例的几个部分。
dr=helperdraw旋转;
在三个维度的旋转
所有三维旋转都可以由旋转轴和绕旋转轴旋转的角度来定义。考虑最左边的图中一个茶壶的三维图像。茶壶在第二个图中围绕z轴旋转45度。在第三张图中显示了一个更复杂的绕轴[1 0 1]旋转15度。四元数封装了轴和旋转角度,并有一个操作这些旋转的代数。这个四元数类,而这个例子中,用“右手法则”公约定义旋转。即,从原点观察时正旋转是顺时针方向绕旋转轴线。
Drawteapotions博士;

点旋转
茶壶的顶点围绕参考系的旋转轴旋转,考虑一个点(0.7,0.5)绕Z轴旋转30度。
数字;dr.draw2DPointRotation(GCA);

框架旋转
从某种意义上说,帧旋转与点旋转相反。在帧旋转中,对象的点保持固定,但参考帧旋转。再次,考虑点(0.7,0.5)。现在,参照系绕Z轴旋转30度。请注意,虽然点(0.7,0.5)保持固定,但它在新的旋转参照系中具有不同的坐标。
图形博士(gca);

方向
取向是指物体相对于参考的帧的的角位移。典型地,取向由引起从起始取向这个角位移的旋转说明。在此示例中,取向被定义为发生在母参考帧中的量,以一个子帧参考的旋转。取向通常被给定为一个四元数,旋转矩阵,设置欧拉角,或者旋转矢量。孩子参照系是相对父框架旋转:考虑定向框架的旋转是有用的。
考虑一个例子,其中子参考帧围绕矢量[1/3,2/3,2/3 ]旋转30度。
数字;dr.draw3DOrientation(GCA,[1/3 2/3 2/3],30);

四元数
四元数是这种形式的数
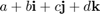
在哪里
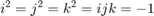
和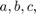 和
和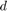 是实数。在这个例子中的休息,四位数字
是实数。在这个例子中的休息,四位数字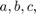 和
和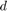 被称为部分四元数的一种形式。
被称为部分四元数的一种形式。
用于旋转和方向的四元数
轴和旋转角度被封装在四元数部分中。为单位矢量旋转轴[x,Y,Z],和旋转角度 ,描述此旋转的四元数为
,描述此旋转的四元数为
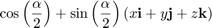
注意,要用四元数来描述旋转,四元数必须是单位四元数.单位四元数的范数为1,范数定义为
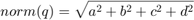
在MATLAB中有多种构造四元数的方法,例如:
q1=四元数(1,2,3,4)
Q1 =四元数1 + 2I + 3J + 4K
四元数数组的制作方法相同:
四元数([1 10;-1 1], [2 20;-2 2], [3 30;-3 3], [4 40;4 4])
Ans = 2x2四元数数组1 + 2i + 3j + 4k 10 + 20i + 30j + 40k -1 - 2i - 3j - 4k 1 + 2i + 3j + 4k
有四列的数组也可以用来构造四元数,每一列表示四元数的一部分:
qmgk=四元数(魔法(4))
qmgk = 4×1四元阵列16 + 2I + 3J + 13K 5 + 11i的+ 10J + 8K 9 + 7I + 6J + 12K 4 + 1141 + 15J + 1K
四元数可以被索引和操作就像任何其他阵列:
qmgk(3)
ANS =四元数9 + 7I + 6J + 12K
重塑(qmgk,2,2)
Ans = 2x2四元数数组16 + 2i + 3j + 13k 9 + 7i + 6j + 12k 5 + 11i + 10j + 8k 4 + 14i + 15j + 1k
[q1;q1]
Ans = 2x1四元数数组1 + 2i + 3j + 4k 1 + 2i + 3j + 4k
四元数数学
四元数具有定义良好的算术运算。加法和减法类似于复数:部分是独立加/减的。由于前面的等式,乘法更为复杂:
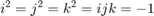
这意味着四元数的乘法是不可交换的。也就是说,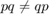 对于四元
对于四元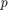 和
和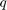 .然而,每一个四元数具有乘法逆,所以四元数可以划分。的数组
.然而,每一个四元数具有乘法逆,所以四元数可以划分。的数组四元数类可以在MATLAB中进行加、减、乘和除。
Q =四元数(1,2,3,4);P =四元数(-5,6,-7,8-);
除了
p+q
ans=四元数-4+8i-4j+12k
减法
p-q
ans=四元数-6+4i-10j+4k
乘法
p *
ans=四元数-28-56i-30j+20k
按相反顺序乘法(注意不同的结果)
q * p
Ans =四元数-28 + 48i - 14j - 44k
权划分P通过Q相当于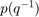 .
.
p、 /q
ANS =四元数0.6 + 2.2667i + 0.53333j - 0.13333k
左部Q通过P相当于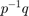 .
.
p。\问
Ans =四元数0.10345 + 0.2069i + 0j - 0.34483k
四元数的共轭是通过对每个非实数部分求反形成的,类似于复数的共轭:
缀(p)的
Ans =四元数-5 - 6i + 7j - 8k
四元数可以在MATLAB中标准化:
pnormed=标准化(p)
pnormmed =四元数-0.37905 + 0.45486i - 0.53067j + 0.60648k
标准(pnormed)
ans = 1
具有四元数的点和帧旋转
四元数可以用来旋转点在参考静态帧,或以旋转的参考自身的帧。这个旋转点函数旋转一个点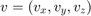 使用四元数q通过下列方程:
使用四元数q通过下列方程:
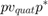
在哪里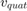 是
是
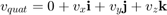
和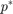 表示四元数共轭。请注意,上面的四元数乘法结果是四元数的实部,
表示四元数共轭。请注意,上面的四元数乘法结果是四元数的实部, ,等于0。这个
,等于0。这个 ,
, ,
,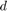 部分结果形成旋转点(
部分结果形成旋转点( ,
, ,
,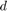 ).
).
考虑上面的点旋转的例子。点(0.7,0.5)绕z轴旋转30度。在三维空间中,这个点的z坐标为0z。使用轴-角公式,可以用[0 0 1]作为旋转轴构造四元数。
ang=deg2rad(30);q=四元数(cos(ang/2),0,0,sin(ang/2));pt=[0.7,0.5,0];% z坐标在X-Y平面上为0ptrot = rotatepoint(Q,PT)
ptrot=0.3562 0.7830 0
同样地rotateframe函数取四元数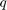 和点
和点 计算
计算
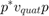
再次上述四元数相乘的结果以四元数与0实部。这 ( ,
, ,
,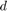 )结果的一部分构成点的坐标
)结果的一部分构成点的坐标 在新的旋转的参考系中。使用
在新的旋转的参考系中。使用四元数班级:
Ptframerot = rotateframe(q, pt)
ptframerot = 0.8562 0.0830 0
由于点和帧旋转方程的对称性,四元数及其共轭具有相反的效果。通过共轭旋转“撤消”旋转。
rotateframe(缀(q)中,ptframerot)
ANS = 0.7000 0.5000 0
由于方程的对称性,这段代码执行相同的旋转。
旋转点(q,ptframerot)
ANS = 0.7000 0.5000 0
其他旋转表示
常旋转和取向使用替代来描述:欧拉角,旋转矩阵,和/或旋转矢量。所有这些互操作在MATLAB四元数。
欧拉角被频繁使用,因为它们很容易解释。考虑的参考框架旋转了绕Z轴30度,然后绕Y轴20度,然后-50绕X轴度。这里注意,并在整个围绕各轴的旋转是固有的:每个随后的旋转是围绕所述新创建的组轴。换句话说,第二旋转是围绕“新的” Y轴由所述第一旋转所产生,而不是周围的原始Y轴。
数字;euld = [30 20 -50]。dr.drawEulerRotation(GCA,euld);
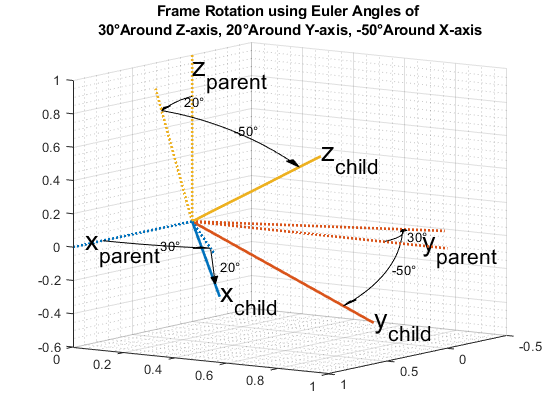
为了建立从这些欧拉角为框架旋转的目的,四元数,使用四元数构造函数。因为旋转的顺序是先绕z轴旋转,然后绕新的y轴旋转,最后绕新的x轴旋转,所以使用“ZYX”旗帜。
qeul =四元数(函数(euld),“欧拉”,“ZYX”,“框架”)
qeul=四元数0.84313-0.44275i+0.044296j+0.30189k
这个“欧拉”标志指示第一个参数以弧度为单位。如果参数是度数,则使用“欧勒德”旗帜。
qeuld=四元数(euld,“欧勒德”,“ZYX”,“框架”)
qeuld=四元数0.84313-0.44275i+0.044296j+0.30189k
要转换回Euler角度,请执行以下操作:
rad2deg(欧拉(qeul,“ZYX”,“框架”))
Ans = 30.000 20.0000 -50.000
同样,欧勒德方法可以使用。
eulerd(qeul,“ZYX”,“框架”)
Ans = 30.000 20.0000 -50.000
或者,相同的旋转可以表示为旋转矩阵:
rmat=rotmat(qeul,“框架”)
RMAT = 0.8138 0.4698 -0.3420 -0.5483 0.4257 -0.7198 -0.1926 0.7733 0.6040
转换回四元数的过程类似:
四元数(rmat'rotmat',“框架”)
Ans =四元数0.84313 - 0.44275i + 0.044296j + 0.30189k
就像四元数可以用于点或帧旋转一样,它也可以转换为用于点或帧旋转的旋转矩阵(或欧拉角集)。点旋转的旋转矩阵是坐标系旋转的转置矩阵。要在旋转表示之间进行转换,必须指定'观点'或“框架”.
对于本实施例的点旋转部的旋转矩阵为:
rotmatPoint=rotmat(q,'观点')
旋转点=0.8660-0.5000 0.5000 0.8660 0 0 1.0000
为了找到旋转点的位置,正确的乘旋转点通过转置阵pt.
rotmatPoint * (pt)
ans=0.3562 0.7830 0
对于本实施例的框架旋转部的旋转矩阵为:
rotmatFrame=rotmat(q,“框架”)
rotmatFrame = 0.8660 0.5000 0 -0.5000 0.8660 0 0 0 1.0000
为了找到该点的位置在旋转参考系中,右乘rotmatFrame通过转置阵pt.
旋转框架*(pt')
ANS = 0.8562 0.0830 0
旋转向量是一种替代的、紧凑的旋转封装。旋转向量只是一个三元素向量,表示单位长度的旋转轴,该旋转轴按旋转角度(弧度)放大。旋转向量没有与帧度或点度相关的属性。要转换为旋转向量,请执行以下操作:
rv=rotvec(qeul)
rv=-0.9349 0.0935 0.6375
要转换为四元数:
四元数(rv,'rotvec')
Ans =四元数0.84313 - 0.44275i + 0.044296j + 0.30189k
距离
四元数比欧拉角的一个优点是没有不连续。欧拉角有不连续点,它的变化取决于所使用的惯例。这个经销函数通过两个不同的四元数比较旋转的效果。结果是一个介于0到0之间的数字π.考虑从欧拉角建造两个四元:
eul1=[0,10,0];eul2=[0,15,0];qdist1=四元数(deg2rad(eul1),“欧拉”,“ZYX”,“框架”);qdist2=四元数(deg2rad(eul2),“欧拉”,“ZYX”,“框架”);
减去欧拉角,你可以看到没有绕z轴或x轴旋转。
eul2——eul1
ans=0 5 0
这两个旋转之间的差是绕y轴5度。这个经销这也显示了差异。
rad2deg (dist (qdist1 qdist2))
ans=5.0000
为欧拉角如eul1和eul2中,计算的角距离是微不足道的。一个更复杂的例子中,其跨越的欧拉角的不连续,是:
eul3=[0,89,0];eul4=[180,89,180];qdist3=四元数(deg2rad(eul3),“欧拉”,“ZYX”,“框架”);qdist4 =四元数(函数(eul4),“欧拉”,“ZYX”,“框架”);
虽然eul3和eul4表示几乎相同的方向,简单的欧拉角减法给人的印象是这两个方向相距很远。
Euldiff = eul4 - eul3
euldiff=180 0 180
使用经销在四元数表明,只有在这些旋转两度差函数:
euldist=rad2deg(区(qdist3,qdist4))
euldist=2.0000
四元数和它的负数表示相同的旋转。这在减去四元数时并不明显,但是经销功能使得它清除。
qpos=四元数(-cos(pi/4),0,0,sin(pi/4))
qpos=四元数-0.70711+0i+0j+0.70711k
qneg=-qpos
qneg=四元数0.70711+0i+0j-0.70711k
qdiff=qpos-qneg
qdiff=四元数-1.4142+0i+0j+1.4142k
dist (qpo qneg)
ANS = 0
金宝app支持功能
这个四元数类可以有效地在MATLAB中描述旋转和方向。函数可以找到四元数支持的函数的完整列表金宝app方法功能:
方法(“四元数”)
类四元数的方法:角度ismatrix prod cat四元数类隐含的isrow rdivide compact isscalar reconj isvector rotateframe ctranspose ldivide rotatepoint disp length rotmat dist log rotvec double meanrot rotvecd eq - single euler mtimes size eulerd slerp ne times horzcat范数转置iscolumn normalize uminus isempty nummelvalidateattributes isequal parts vertcat isequaln permute isfinite plus isinf power静态方法:1 0
