人口生态系统

在所有三个人口系统调查我们有趣的两个物种随时间的人口。模型,让x1 (t)和x2 (t)表示各自的物种的个体数量在时间t。让l1和l2表示出生率与x1 (t)和x2 (t),分别都假定为常数。物种的死亡率都取决于食品的可用性,如果捕食者存在,被吃掉的风险。经常(一般而言),物种的死亡率我(i = 1或2)可以编写ui (x1 (t), x2 (t)),在ui(.)是一些适当的函数。在实践中,这意味着ui (x1 (t), x2 (t)) * xi (t)的动物物种的我每次都死了。这些语句的净效应可以概括在一种状态空间模型结构:(时间序列):

d

——x1 (t) = l1 * x1 (t) - u1 (x1 (t), x2 (t)) * x1 (t)

dt

d

——x2 (t) = l2 * x2 (t) - u2 (x1 (t), x2 (t)) * x2 (t)

dt

这里是自然选择两种状态输出,即。,我们让日元(t) = x1 (t)和y2 (t) = x2 (t)。

. 1。两个物种争夺相同的食物

两个物种争夺同样的食物,那么它就是整个物种的种群控制食品的可用性,进而他们的死亡率。一个简单而常用的方法是假定死亡率可以写成:

ui (x1 (t) x2 (t)) = gi + di * (x1 (t) + x2 (t))

两个物种(i = 1或2),胃肠道和di未知参数。完全这给了状态空间结构:

d

——x1 (t) = (l1-g1) * x1 (t) - d1 * (x1 (t) + x2 (t)) * x1 (t)

dt

d

——x2 (t) = (l2-g2) * x2 (t) - d2 * (x1 (t) + x2 (t)) * x2 (t)

dt

立即这个结构问题是l1, g1, l2, g2不能单独确定。我们只能希望确定p1 = l1-g1和p3 = l2-g2。,也让p2 = d1和p4 = d2,一个得到reparameterized模型结构:

d

- - - x1 (t) = p1 * x1 (t) - p2 * (x1 (t) + x2 (t)) * x1 (t)

dt

d

——x2 (t) = p3 * x2 (t) - p4 * (x1 (t) + x2 (t)) * x2 (t)

dt

日元(t) = x1 (t)

y2 (t) = x2 (t)

在第一个人口我们诉诸于MATLAB文件示例建模。上面的方程然后进入一个MATLAB文件,preys_m。米,以下内容。

函数(dx, y) = preys_m (t, x, u, p1, p2, p3, p4,变长度输入宗量)

% PREYS_M两个物种争夺相同的食物。

%输出方程。

y = [x (1);…%的猎物物种1。

x (2)……%猎物2。

];

%状态方程。

dx = [p1 * x (1) p2 * x (x (1) + (2)) * x (1);…%的猎物物种1。

p3 * x (2) p4 * x (x (1) + (2)) * x (2)……%猎物2。

];

MATLAB文件,以及一个初始参数向量,一个适当的初始状态,一些行政信息下美联储作为输入IDNLGREY对象的构造函数。请注意,这两个参数的初始值和初始状态被指定为结构数组与禁食(参数对象的数量=数量的参数如果所有参数都是标量)和Nx(州)元素,分别。通过这些结构数组可以完全指定非默认属性值(“名称”、“单位”、“价值,”最大”、“最小”,和“固定”)每个参数和初始状态。这里我们有分配每个初始状态的“最小值”值为零(人口是积极的!),并指定默认初始状态都是估计。

文件名=“preys_m”;%文件描述模型结构。订单= (2 0 2);%模型[纽约νnx]命令。参数=结构(“名字”,{物种的生存因素,1 '“死亡因素,物种1”…物种的生存因素,2》《死亡因素,物种2》},…“单位”,{1 /年的1 /年的1 /年的1 /年的},…“价值”{1.8 0.8 1.2 0.8},…“最低”,{负负负无穷},…“最大”,{正正正正},…“固定”,{假假假假});%所有4参数估计。InitialStates =结构(“名字”,{“人口,物种1”《人口、物种2》},…“单位”,{的大小(千)的大小(千)},…“价值”{0.2 - 1.8},…“最低”,{0 0},…“最大”{正正无穷},…“固定”,{假假});%初始状态估计。t = 0;%的时间连续系统。nlgr = idnlgrey(文件名、秩序、参数、InitialStates Ts,…“名字”,“两个物种争夺同样的食物”,…“OutputName”,{“人口,物种1”《人口、物种2》},…“OutputUnit”,{的大小(千)的大小(千)},…“TimeUnit”,“年”);

当前命令可用于视图初始模型的信息:

礼物(nlgr);

nlgr =连续时间非线性灰色矩形模型定义为“preys_m”(MATLAB文件):dx / dt = F (t) x (t), p1,…p4) y (t) = H (t) x (t), p1,…,p4) + e(t) with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4). States: Initial value x(1) Population, species 1(t) [Size (in t..] xinit@exp1 0.2 (estimated) in [0, Inf] x(2) Population, species 2(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf] Outputs: y(1) Population, species 1(t) [Size (in thousands)] y(2) Population, species 2(t) [Size (in thousands)] Parameters: Value p1 Survival factor, species 1 [1/year] 1.8 (estimated) in [-Inf, Inf] p2 Death factor, species 1 [1/year] 0.8 (estimated) in [-Inf, Inf] p3 Survival factor, species 2 [1/year] 1.2 (estimated) in [-Inf, Inf] p4 Death factor, species 2 [1/year] 0.8 (estimated) in [-Inf, Inf] Name: Two species competing for the same food Status: Created by direct construction or transformation. Not estimated. More information in model's "Report" property.

由信用证。输入输出数据

我们下一个负载(模拟,虽然噪声损坏)数据和创建一个IDDATA对象描述一个特定的情况下两个物种争夺同样的食物。这些数据集包含201个数据样本覆盖20年的进化。

负载(fullfile (matlabroot“工具箱”,“识别”,“iddemos”,“数据”,“preydata”));z = iddata (y, [], 0.1,“名字”,“两个物种争夺同样的食物”);集(z,“OutputName”,{“人口,物种1”,《人口、物种2》},…“Tstart”0,“TimeUnit”,“年”);

出具。初始的两种模型的性能

模拟与初始模型清楚地表明,它无法应付真正的种群动态。看到阴谋图。IDNLGREY模型的时间序列类型注意模型的输出是由初始状态决定。

比较(z nlgr 1);

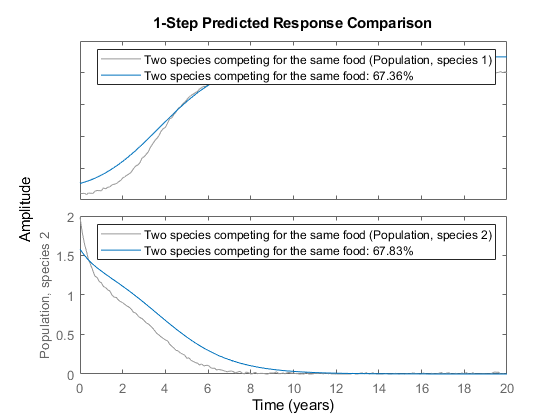
图1:比较真实的输出和初始的两种模型的模拟输出。

各。参数估计

为了克服,而表现不佳的初始模型进行估计4未知参数和2使用NLGREYEST初始状态。使用NLGREYESTOPTIONS指定评估选项;在这种情况下“显示”设置为“上”,这意味着评估进展信息显示在窗口的进展。您可以使用NLGREYESTOPTIONS指定算法的基本属性,如‘GradientOptions’,‘SearchMethod’,‘MaxIterations’,‘宽容’,‘显示’。

选择= nlgreyestOptions;opt.Display =“上”;opt.SearchOptions。MaxIterations = 50;nlgr = nlgreyest (z, nlgr,选择);

本。估计两种模型的性能

估计的参数和初始状态值很符合那些用于生成真正的输出数据:

disp (“真正的估计参数向量”);

真正的估计参数向量

ptrue = [2;1;1;1);流(“% 6.3 f % 6.3 f \ n”[ptrue ';getpvec (nlgr) '));

2.000 2.004 1.000 1.002 1.000 1.018 1.000 1.010

disp (' ');

disp (“真估计初始状态”);

正确估计初始状态

x0true = (0.1;2);流(“% 6.3 f % 6.3 f \ n”[x0true ';cell2mat (getinit (nlgr,“价值”))));

0.100 0.101 2.000 1.989

进一步评估的质量模型,说明了改进的初始模型相比)我们还模拟估计模型。模拟输出比较一块真正的输出窗口。可以看到,估计模型相当好。

比较(z nlgr 1);

图2:比较真实的输出和估计的两种模型的模拟输出。

提供进一步的信息估计模型,例如,关于参数的不确定性,和相关的其他估计量,如损失函数和Akaike消防工程(最终的预测误差)措施。

礼物(nlgr);

nlgr =连续时间非线性灰色矩形模型定义为“preys_m”(MATLAB文件):dx / dt = F (t) x (t), p1,…p4) y (t) = H (t) x (t), p1,…,p4) + e(t) with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4). States: Initial value x(1) Population, species 1(t) [Size (in t..] xinit@exp1 0.100729 (estimated) in [0, Inf] x(2) Population, species 2(t) [Size (in t..] xinit@exp1 1.98855 (estimated) in [0, Inf] Outputs: y(1) Population, species 1(t) [Size (in thousands)] y(2) Population, species 2(t) [Size (in thousands)] Parameters: ValueStandard Deviation p1 Survival factor, species 1 [1/year] 2.00429 0.00971109 (estimated) in [-Inf, Inf] p2 Death factor, species 1 [1/year] 1.00235 0.00501783 (estimated) in [-Inf, Inf] p3 Survival factor, species 2 [1/year] 1.01779 0.0229598 (estimated) in [-Inf, Inf] p4 Death factor, species 2 [1/year] 1.0102 0.0163506 (estimated) in [-Inf, Inf] Name: Two species competing for the same food Status: Termination condition: Near (local) minimum, (norm(g) < tol).. Number of iterations: 5, Number of function evaluations: 6 Estimated using Solver: ode45; Search: lsqnonlin on time domain data "Two species competing for the same food". Fit to estimation data: [98.42;97.92]% FPE: 7.747e-09, MSE: 0.0001743 More information in model's "Report" property.

责任。一个经典的捕食系统

现在假设第一个物种生活在第二个。的可用性物种的食物然后1 x2 (t)成正比(物种的个体数量2),这意味着1物种的死亡率减少当x2 (t)增加。这一事实被简单的表达式:

u1 (x1 (t), x2 (t)) = g1 - a1 * x2 (t)

g1和a1未知参数。同样,物种的死亡率2将会增加当第一个物种的个体数量的增加,例如,根据:

u2 (x1 (t), x2 (t)) = g2 + a2 * x1 (t)

g2和a2两个未知参数。使用线性出生率假定上面得到状态空间结构:

d

——x1 (t) = (l1-g1) * x1 (t) + a1 * x2 (t) * x1 (t)

dt

d

——x2 (t) = (l2-g2) * x2 (t) - a2 * x1 (t) * x2 (t)

dt

作为人口在前面的例子,这里也不可能来唯一地标识的六个人参数。与同样的reparameterization在上述情况下,即,p1 = l1-g1, p2 = a1, p3 = l2-g2, and p4 = a2, the following model structure is obtained:

d

- - - x1 (t) = p1 * x1 (t) + p2 * x2 (t) * x1 (t)

dt

d

——x2 (t) = p3 * x2 (t) - p4 * x1 (t) * x2 (t)

dt

日元(t) = x1 (t)

y2 (t) = x2 (t)

这样能更好的从一个估计的观点。

这一次我们这个信息输入到一个C MEX-file predprey1_c.c命名。模型文件结构作为标准IDNLGREY C MEX-file(见例子题为“创建IDNLGREY模型文件”或idnlgreydemo2.m),与国家和输出更新功能,compute_dx compute_y,如下。

空白compute_dx(双* dx,双t,双* x,双* * p,

const mxArray * auxvar)

{

/ *获取模型参数。* /

双* p1, p2, p3, p4 *;

p1 = p [0];/ *生存因素,捕食者。* /

p2 = p [1];/ *死亡因素,捕食者。* /

p3 = p [2];/ *生存因素,猎物。* /

p4 = p [3];/ *死亡因素,猎物。* /

/ * x[0]:食肉动物物种。* /

/ * x[1]:猎物物种。* /

dx [0] = p1 [0] * x [0] + p2 [0] * x [1] * [0];

dx [1] = p3 [0] * x [1] p4 [0] * x [0] * [1];

}

/ *输出方程。* /

空白compute_y(双* y,双t,双* x,双* * p,

const mxArray * auxvar)

{

/ * y[0]:食肉动物物种。* /

/ * y[1]:猎物。* /

y [0] = x [0];

y [1] = x [1];

}

从时间序列的模型类型,无论是compute_dx还是compute_y包括u在输入参数列表。事实上,predprey1_c的主界面功能。c,甚至不宣布u即使空([])总是传递给IDNLGREY predprey1_c的方法。

编译C MEX-file,连同一个初始参数向量,一个适当的初始状态,和一些行政信息作为输入参数下美联储IDNLGREY对象构造函数:

文件名=“predprey1_c”;%文件描述模型结构。订单= (2 0 2);%模型[纽约νnx]命令。参数=结构(“名字”,{“生存因素,捕食者”“死亡因素,捕食者”…“生存因素,猎物”“死亡因素,猎物”},…“单位”,{1 /年的1 /年的1 /年的1 /年的},…“价值”{-1.1 0.9 1.1 0.9},…“最低”,{负负负无穷},…“最大”,{正正正正},…“固定”,{假假假假});%所有4参数估计。InitialStates =结构(“名字”,{“人口,捕食者”“人口,猎物”},…“单位”,{的大小(千)的大小(千)},…“价值”{1.8 - 1.8},…“最低”,{0 0},…“最大”{正正无穷},…“固定”,{假假});%初始状态估计。t = 0;%的时间连续系统。nlgr = idnlgrey(文件名、秩序、参数、InitialStates Ts,…“名字”,“古典1捕食者- 1猎物系统”,…“OutputName”,{“人口,捕食者”,“人口,猎物”},…“OutputUnit”,{的大小(千)的大小(千)},…“TimeUnit”,“年”);

捕食者猎物模型下通过当前文本查看命令。

礼物(nlgr);

nlgr =连续时间非线性灰色矩形模型定义为“predprey1_c”(MEX-file): dx / dt = F (t) x (t), p1,…p4) y (t) = H (t) x (t), p1,…,p4) + e(t) with 0 input(s), 2 state(s), 2 output(s), and 4 free parameter(s) (out of 4). States: Initial value x(1) Population, predators(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf] x(2) Population, preys(t) [Size (in t..] xinit@exp1 1.8 (estimated) in [0, Inf] Outputs: y(1) Population, predators(t) [Size (in thousands)] y(2) Population, preys(t) [Size (in thousands)] Parameters: Value p1 Survival factor, predators [1/year] -1.1 (estimated) in [-Inf, Inf] p2 Death factor, predators [1/year] 0.9 (estimated) in [-Inf, Inf] p3 Survival factor, preys [1/year] 1.1 (estimated) in [-Inf, Inf] p4 Death factor, preys [1/year] 0.9 (estimated) in [-Inf, Inf] Name: Classical 1 predator - 1 prey system Status: Created by direct construction or transformation. Not estimated. More information in model's "Report" property.

B.2。输入输出数据

我们的下一步是负载(模拟,虽然噪声损坏)数据和创建一个IDDATA对象描述这个特殊的捕食者-猎物的情况。这个数据集还包含了201个数据样本覆盖20年的进化。

负载(fullfile (matlabroot“工具箱”,“识别”,“iddemos”,“数据”,“predprey1data”));z = iddata (y, [], 0.1,“名字”,“古典1捕食者- 1猎物系统”);集(z,“OutputName”,{“人口,捕食者”,“人口,猎物”},…“Tstart”0,“TimeUnit”,“年”);

B.3。最初的经典捕食模型的性能

初始模型的仿真表明,它不能准确地应对真正的种群动态。看到图窗口。

比较(z nlgr 1);

图3:比较真实的输出和初始的古典捕食模型的模拟输出。

B.4。参数估计

提高初始模型的性能我们继续估计4未知参数和2使用NLGREYEST初始状态。

nlgr = nlgreyest (z, nlgr nlgreyestOptions (“显示”,“上”));

B.5。估计经典捕食模型的性能

估计的参数和初始状态值非常接近那些被用来生成真正的输出数据:

disp (“真正的估计参数向量”);

真正的估计参数向量

ptrue = [1;1;1;1);流(“% 6.3 f % 6.3 f \ n”[ptrue ';getpvec (nlgr) '));

-1.000 -1.000 1.000 1.000 1.000 1.000 1.000 0.999

disp (' ');

disp (“真估计初始状态”);

正确估计初始状态

x0true = [2;2);流(“% 6.3 f % 6.3 f \ n”[x0true ';cell2mat (getinit (nlgr,“价值”))));

2.000 2.002 2.000 2.000

进一步评估模型的质量(并说明改进初始模型相比)我们还模拟估计模型。模拟输出比较一块真正的输出窗口。我们可以看到,估计模型相当好。

比较(z nlgr 1);

图4:比较真实的输出和模拟估计古典捕食模型的输出。

正如所料,PE返回的预测误差都很小,一个随机的本质。

体育(z, nlgr);

图5:获得的预测错误的估计IDNLGREY古典捕食模型。

C.1。猎物的捕食系统拥挤

过去人口研究也致力于1捕食者和猎物系统,区别在于,我们在这里介绍的一个术语p5 * x2 (t) ^ 2代表迟钝的猎物增长由于拥挤。reparameterized模型结构从前面的例子就补充这个拥挤条件:

d

- - - x1 (t) = p1 * x1 (t) + p2 * x2 (t) * x1 (t)

dt

d

——x2 (t) = p3 * x2 (t) - p4 * x1 (t) * x2 (t) - p5 * x2 (t) ^ 2

dt

日元(t) = x1 (t)

y2 (t) = x2 (t)

这些方程的解释本质上是上面的一样,除了没有捕食者猎物种群的增长将保持在海湾。

新的建模情况反映在一个C MEX-file称为predprey2_c。predprey1_c.c c,这几乎是一样的。除了更改相关模型参数的数量(5而不是4),主要的区别在于compute_dx状态更新功能:

/ *状态方程。* /

空白compute_dx(双* dx,双t,双* x,双* * p,

const mxArray * auxvar)

{

/ *获取模型参数。* /

双* p1, p2, p3, p4, * p5;

p1 = p [0];/ *生存因素,捕食者。* /

p2 = p [1];/ *死亡因素,捕食者。* /

p3 = p [2];/ *生存因素,猎物。* /

p4 = p [3];/ *死亡因素,猎物。* /

p5 = p [4];/ *拥挤因素,猎物。* /

/ * x[0]:食肉动物物种。* /

/ * x[1]:猎物物种。* /

dx [0] = p1 [0] * x [0] + p2 [0] * x [1] * [0];

dx [1] = p3 [0] * x [1] p4 [0] * x [0] * [1] p5[0] *战俘(x [1], 2);

}

注意,添加缺陷项计算是p5[0] *战俘(x [1], 2)。函数战俘(的力量。,。) is defined in the C library math.h, which must be included at the top of the model file through the statement #include "math.h" (this is not necessary in predprey1_c.c as it only holds standard C mathematics).

编译C MEX-file,连同一个初始参数向量,一个适当的初始状态,和一些行政信息作为输入参数下美联储IDNLGREY对象构造函数:

文件名=“predprey2_c”;%文件描述模型结构。订单= (2 0 2);%模型[纽约νnx]命令。参数=结构(“名字”,{“生存因素,捕食者”“死亡因素,捕食者”…“生存因素,猎物”“死亡因素,猎物”…“拥挤因素,猎物”},…“单位”,{1 /年的1 /年的1 /年的1 /年的1 /年的},…“价值”{-1.1 0.9 1.1 0.9 0.2},…“最低”,{负负负负无穷},…“最大”,{正正正正正},…“固定”,{假假假假假});%所有5参数估计。InitialStates =结构(“名字”,{“人口,捕食者”“人口,猎物”},…“单位”,{的大小(千)的大小(千)},…“价值”{1.8 - 1.8},…“最低”,{0 0},…“最大”{正正无穷},…“固定”,{假假});%初始状态估计。t = 0;%的时间连续系统。nlgr = idnlgrey(文件名、秩序、参数、InitialStates Ts,…“名字”,1捕食者- 1猎物系统表现出拥挤的,…“OutputName”,{“人口,捕食者”,“人口,猎物”},…“OutputUnit”,{的大小(千)的大小(千)},…“TimeUnit”,“年”);

通过输入模型对象的名字(nlgr)基本信息模型是在命令窗口中显示。注意,像以前一样,现在(nlgr)提供了一个更全面的模型的总结。

nlgr

nlgr =连续时间非线性灰色矩形模型定义为“predprey2_c”(MEX-file): dx / dt = F (t) x (t), p1,…、p5) y (t) = H (t) x (t), p1,…,p5) + e(t) with 0 input(s), 2 state(s), 2 output(s), and 5 free parameter(s) (out of 5). Name: 1 predator - 1 prey system exhibiting crowding Status: Created by direct construction or transformation. Not estimated.

C.2。输入输出数据

接下来我们负载(模拟,虽然噪声损坏)数据和创建一个IDDATA对象描述这种拥挤的捕食者-猎物的情况。这些数据集包含201个数据样本覆盖20年的进化。

负载(fullfile (matlabroot“工具箱”,“识别”,“iddemos”,“数据”,“predprey2data”));z = iddata (y, [], 0.1,“名字”,1捕食者- 1猎物系统表现出拥挤的);集(z,“OutputName”,{“人口,捕食者”,“人口,猎物”},…“Tstart”0,“TimeUnit”,“年”);

C.3。初始的捕食模型的性能与拥挤的猎物

模拟与初始模型清楚地表明,它无法应付真正的种群动态。见图。

clf比较(z nlgr 1);

图6:比较真实的输出和初始的捕食模型的模拟输出与拥挤的猎物。

C.4。参数估计

提高性能的初始模型进行估计5未知参数和2初始状态。

nlgr = nlgreyest (z, nlgr nlgreyestOptions (“显示”,“上”));

C.5。估计捕食模型的性能与拥挤的猎物

估计的参数值和初始状态又非常接近那些被用来生成真正的输出数据:

disp (“真正的估计参数向量”);

真正的估计参数向量

ptrue = [1;1;1;1;0.1);流(“% 6.3 f % 6.3 f \ n”[ptrue ';getpvec (nlgr) '));

-1.000 -1.000 1.000 1.001 1.000 1.002 1.000 1.002 0.100 0.101

disp (' ');

disp (“真估计初始状态”);

正确估计初始状态

x0true = [2;2);流(“% 6.3 f % 6.3 f \ n”[x0true ';cell2mat (getinit (nlgr,“价值”))));

2.000 2.003 2.000 2.002

进一步评估的质量模型,说明了改进的初始模型相比)我们还模拟估计模型。模拟输出比较一块真正的输出窗口。我们可以看到,估计模型相当好。

比较(z nlgr 1);

图7:比较真实的估计捕食模型的输出和模拟输出与拥挤的猎物。

我们结束第三个人口例子展示返回的模型信息。

礼物(nlgr);

nlgr =连续时间非线性灰色矩形模型定义为“predprey2_c”(MEX-file): dx / dt = F (t) x (t), p1,…、p5) y (t) = H (t) x (t), p1,…,p5) + e(t) with 0 input(s), 2 state(s), 2 output(s), and 5 free parameter(s) (out of 5). States: Initial value x(1) Population, predators(t) [Size (in t..] xinit@exp1 2.00281 (estimated) in [0, Inf] x(2) Population, preys(t) [Size (in t..] xinit@exp1 2.00224 (estimated) in [0, Inf] Outputs: y(1) Population, predators(t) [Size (in thousands)] y(2) Population, preys(t) [Size (in thousands)] Parameters: Value Standard Deviation p1 Survival factor, predators [1/year] -0.999914 0.00280581 (estimated) in [-Inf, Inf] p2 Death factor, predators [1/year] 1.00058 0.00276684 (estimated) in [-Inf, Inf] p3 Survival factor, preys [1/year] 1.0019 0.00272154 (estimated) in [-Inf, Inf] p4 Death factor, preys [1/year] 1.00224 0.00268423 (estimated) in [-Inf, Inf] p5 Crowding factor, preys [1/year] 0.101331 0.0005023 (estimated) in [-Inf, Inf] Name: 1 predator - 1 prey system exhibiting crowding Status: Termination condition: Change in cost was less than the specified tolerance.. Number of iterations: 8, Number of function evaluations: 9 Estimated using Solver: ode45; Search: lsqnonlin on time domain data "1 predator - 1 prey system exhibiting crowding". Fit to estimation data: [97.53;97.36]% FPE: 4.327e-08, MSE: 0.0004023 More information in model's "Report" property.

结论

这个例子展示了如何执行IDNLGREY时间序列建模基于MATLAB和墨西哥人模型文件。