离散时间Narendra-Li基准系统

Narendra-Li系统的离散时间方程为：

x1（t+Ts）=（x1（t）/（1+x1（t）^2）+p（1））*sin（x2（t））x2（t）=x2（t）*cos（x2（t））+x1（t）*exp（-（x1（t）^2+x2（t）^2）/p（2））+u（t）^3/（1+u（t）^2+p（3）*cos（x1（t）+x2（t））

y（t）=x1（t）/（1+p（4）*sin（x2（t））+p（5）*sin（x1（t）））

其中，具有输入（t）和输出（t）信号的输入（t）和输出（p）元素是具有输入（t）和输出（p）信号的状态。

IDNL灰色离散时间Narendra-Li模型

从IDNLGREY模型文件的角度来看，连续时间系统和离散时间系统之间没有区别。因此，Narendra Li模型文件必须返回状态更新向量dx和输出y，并且应将t（时间）、x（状态向量）、u（输入）、p（参数）和varargin作为输入参数：

函数[dx，y]=narendrali_m（t，x，u，p，varargin）%narendrali_m是一个离散时间的narendrali基准系统。

%输出方程y=x（1）/（1+p（4）*sin（x（2））+x（2）/（1+p（5）*sin（x（1））；

%状态方程。dx=[（x（1）/（1+x（1）^2）+p（1））*sin（x（2））；…%状态1.x（2）*cos（x（2））+x（1）*exp（-（x（1）^2+x（2）^2）/p（2））…%状态2.+u（1）^3/（1+u（1）^2+p（3）*cos（1）+x（2））…]；

请注意，我们在这里选择将所有5个参数压缩为一个参数向量，其中i:th元素以通常的MATLAB方式引用，即通过p（i）。

以该模型文件为基础，我们接下来创建一个反映建模情况的IDNLGREY对象。这里值得强调的是，模型的离散性是通过Ts（=1秒）的正值指定的。还要注意的是，参数只包含一个元素，一个5乘1的参数向量，并且SETPAR用于指定该向量的所有分量都是严格正的。

文件名=“narendrali_m”;%描述模型结构的文件。顺序=[12]；%型号订单[ny nu nx]。参数={[1.05；7.00；0.52；0.52；0.48]}；%真实初始参数（向量）。初始状态=零（2，1）；%初始状态的初始值。Ts=1；%Ts=1s的时间离散系统。nlgr=IDNLGRY（文件名、顺序、参数、初始状态、Ts、，“姓名”,...“离散时间Narendra-Li基准系统”,...“时间单位”,'s')；nlgr=setpar（nlgr，“最低限度”，{eps（0）*one（5,1）}；

输入的Narendra Li模型结构的摘要可通过当前命令获得：

出席（nlgr）；

nlgr=由narendrali_m（MATLAB文件）定义的离散时间非线性灰箱模型：x（t+Ts）=F（t，u（t），x（t），p1）y（t）=H（t，u（t），x（t），p1）+e（t），具有1个输入、2个状态、1个输出和5个自由参数（共5个）。输入：u（1）（t）状态：初始值x（1）x1（t）xinit@exp1[Inf，Inf]x（2）x2（t）中的0（固定）xinit@exp10（固定）在[-Inf，Inf]输出中：y（1）（t）参数：值p1（1）p1 1.05（估计）in]0，Inf]p1（2）7（估计）in]0，Inf]p1（3）0.52（估计）in]0，Inf]p1（4）0.52（估计）in]0，Inf]p1（5）0.48（估计）在[0，Inf]Name:离散时间Narendra Li基准测试系统采样时间：1秒状态：由直接构造或转换创建。未估计。有关详细信息，请参阅模型的“报告”属性。

输入输出数据

有两个输入-输出数据记录，每个记录有300个样本，一个用于估计，一个用于验证。用于这两个记录的输入向量相同，被选为两个正弦波的总和：

u（t）=sin（2*pi*t/10）+sin（2*pi*t/25）

对于t=0，1，…，299秒，我们创建两个不同的IDDATA对象来保存这两个数据记录，ze用于估计，zv用于验证。

加载（完整文件）（matlabroot，“工具箱”,“识别”,“iddemos”,“数据”,“narendralidata”)); ze=iddata（y1，u，Ts，“启动”, 0,“姓名”,“Narendra Li估算数据”,...“姓名”,“泽”)；zv=iddata（y2，u，Ts，“启动”, 0,“姓名”,“Narendra Li验证数据”,...“姓名”,“zv”);

用于估算的输入输出数据显示在绘图窗口中。

身材(“姓名”，ze.姓名）；地块（ze）；

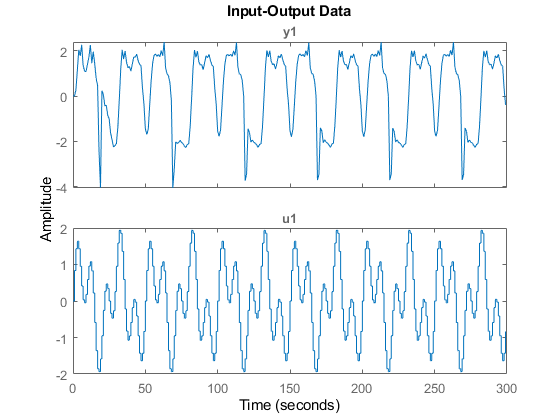
图1：来自Narendra Li基准系统的输入输出数据。

初始Narendra-Li模型的性能

现在让我们使用COMPARE来研究初始Narendra-Li模型的性能。模拟和测量的输出泽和零电压已生成，并适合泽默认情况下显示。使用绘图关联菜单将数据切换到实验零电压. 这两个数据集的拟合度都没有那么差（约74%）。这里我们应该指出，默认情况下比较估计初始状态向量，在这种情况下，一个初始状态向量用于泽还有一个是给你的零电压.

比较（合并（ze，zv），nlgr）；

图2：初始Narendra-Li模型的真实输出和模拟输出之间的比较。

%%4%通过观察通过PE获得的预测误差，我们认识到%初始Narendra-Li模型显示出一些系统性和周期性差异%与真实输出相比。pe（合并（ze，zv），nlgr）；

图3：使用初始Narendra-Li模型获得的预测误差。使用上下文菜单在实验之间切换。

参数估计

为了减少系统差异，我们使用NLGRYEST估计了Narendra-Li模型结构的所有5个参数。仅基于估计数据集ze进行估计。

opt=nlgreyestOptions(“显示”,“开”); nlgr=NLGRYEST（ze、nlgr、opt）；

估计Narendra-Li模型的性能

再次使用COMPARE来研究估计模型的性能，但这次我们使用模型内部存储的初始状态向量（[0；0]用于两个实验），而不进行任何初始状态向量估计。

clf opt=比较选项(“初始条件”,“我是); 比较（合并（ze，zv），nlgr，opt）；

图4：估计的Narendra-Li模型的真实输出和模拟输出之间的比较。

估计后的改善是显著的，通过预测误差图可以最好地说明这一点：

图：pe（合并（ze，zv），nlgr）；

图5：使用估计的Narendra-Li模型获得的预测误差。

估算的Narendra-Li模型的建模能力也通过通过REDIS提供的相关分析得到确认：

身材(“姓名”，[nlgr.Name“：估计模型的残差”])(zv,nlgr);；

图6：使用估计的Narendra-Li模型获得的残差。

事实上，获得的模型参数也非常接近用于生成真实模型输出的参数：

disp(“真实估计参数向量”)；ptrue=[1；8；0.5；0.5；0.5]；fprintf(“%1.4f%1.4f\n”，[ptrue'；getpvec（nlgr'）；

真实估计参数向量1.0000 1.0000 8.0000 8.0082 0.5000 0.5003 0.5000 0.4988 0.5000 0.5018

接下来通过当前命令提供一些额外的模型质量结果（损失函数、Akaike的FPE和模型参数的估计标准偏差）：

出席（nlgr）；

nlgr=由“narendrali_m”（MATLAB文件）定义的离散时间非线性灰箱模型：x（t+Ts）=F（t，u（t），x（t），p1）y（t）=H（t，u（t），x（t），p1）+e（t），具有1个输入、2个状态、1个输出和5个自由参数（共5个）。输入：u（1）u1（t）状态：初始值x（1）x1（t）xinit@exp1[Inf，Inf]x（2）x2（t）中的0（固定）xinit@exp1[Inf]输出中的0（固定）：y（1）y1（t）参数：值标准偏差p1（1）p1 0.99993 0.0117615（估计）in]0，Inf]p1（2）8.00821 0.885988（估计）in]0，Inf]p1（3）0.500319 0.0313092（估计）in]0，Inf]p1（4）0.498842 0.264806（估计值）in]0，Inf]p1（5）0.501761 0.30998（估计值）in]0，Inf]Name:离散时间Narendra Li基准系统采样时间：1秒状态：终止条件：参数变化小于指定公差。。迭代次数：16次，函数评估次数：17次，使用解算器估算：FixedStepDiscrete；搜索：时域数据“Narendra Li估计数据”上的lsqnonlin。适合估算数据：99.44%FPE:9.23e-05，MSE:8.927e-05模型“报告”属性中的更多信息。

对于连续时间输入输出系统，也可以对离散时间输入输出系统使用STEP。让我们对两个不同的步骤级别（1和2）执行此操作：

身材(“姓名”，[nlgr.Name“：估计模型的阶跃响应”])；t=（-5:50）；（nlgr，“b”，t，stepDataOptions(“阶跃振幅”，1）；行（t，步骤（nlgr，t，步骤数据选项(“阶跃振幅”,2)),“颜色”,“g”); 网格在…上；传奇('0 -> 1','0 -> 2',“位置”,“西北”);

图7：使用估计的Narendra-Li模型获得阶跃响应。

通过比较估计的IDNLGREY-Narendra-Li模型与一些基本线性模型的性能，我们总结了这个示例。后一种模型的拟合度大大低于估计的IDNLGREY模型的拟合度。

nk=延迟（ze）；arx22=arx（ze[2 nk]）；%二阶线性ARX模型。arx33=arx（ze，[3 nk]）；%三阶线性ARX模型。arx44=arx（ze[4 nk]）；%四阶线性ARX模型。oe22=oe（ze，[2 nk]）；%二阶线性OE模型。oe33=oe（泽，[3 nk]）；%三阶线性OE模型。oe44=oe（ze，[4 nk]）；%四阶线性OE模型。clf fig=gcf；Pos=图中的位置；图位置=[位置（1:2）*0.7，位置（3）*1.3，位置（4）*1.3]；比较（zv，nlgr，“b”，arx22，“m-”，arx33，m:'，arx44，“我——”,...oe22，“g-”，oe33，g:'，oe44，“g——”);

图8：许多估计的Narendra-Li模型的真实输出和模拟输出之间的比较。

结论

在本例中，我们使用了一个虚拟的离散时间Narendra Li基准系统来说明执行离散时间IDNLGREY建模的基础。