具有雅可比稀疏模式的大型非线性方程组
这个例子展示了如何提供一个雅可比稀疏模式来有效地求解一个大型稀疏方程组。本例使用的目标函数是为一个系统定义的n方程,
要解的方程是
，
．示例使用
．的nlsf1a的辅助函数。本例结束实现目标函数
．
在这个例子中具有雅可比矩阵的大型稀疏非线性方程组求解同一系统时，目标函数具有显式的雅可比矩阵。然而，有时你不能显式地计算雅可比矩阵，但你可以确定雅可比矩阵中哪些元素是非零的。在这个例子中，雅可比矩阵是三对角线的，因为唯一出现在定义中的变量 是 ， , ．雅可比矩阵中唯一非零的部分在主对角线上和它相邻的两条对角线上。雅可比矩阵稀疏模式是一个矩阵，其非零元素对应于雅可比矩阵中的(潜在的)非零元素。
创建一个稀疏的
——- - - - - -
表示雅可比稀疏模式的三对角矩阵。(有关此代码的解释，请参见spdiags．）
N = 1000;E = ones(n,1);Jstr = spdigs ([e e e]，-1:1,n,n);
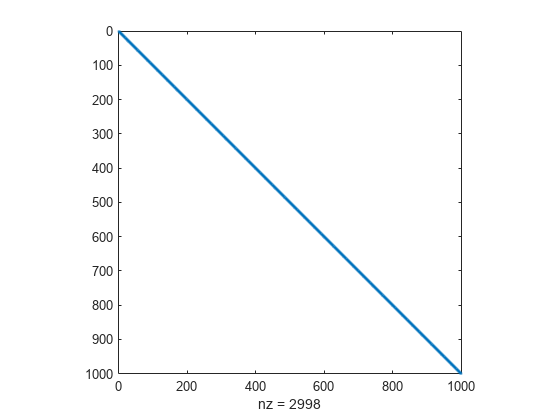
查看结构Jstr．
间谍(Jstr)
集fsolve选项，以使用“信赖域”算法，这是唯一的fsolve可以使用雅可比稀疏模式的算法。
选项= optimoptions(“fsolve”，“算法”，“信赖域”，“JacobPattern”, Jstr);
设定起始点x0到一个含有-1元素的向量。
X0 = -1*ones(n,1);
解决问题。
[x,fval,exitflag,output] = fsolve(@nlsf1a,x0,options);
方程解决。Fsolve是完成的，因为函数值的向量通过函数公差的值测量接近于零，并且通过梯度测量问题显得有规律。
检查所得到的残差范数和函数求值的数量fsolve需要。
disp(规范(fval))
1.0523 e-09
disp (output.funcCount)
25
残差范数接近于零，表明fsolve正确解决问题。函数求值的数量相当少，大约只有24个。将此函数求值的数量与没有提供的雅可比稀疏模式的数量进行比较。
选项= optimoptions(“fsolve”，“算法”，“信赖域”）;[x,fval,exitflag,output] = fsolve(@nlsf1a,x0,options);
方程解决。Fsolve是完成的，因为函数值的向量通过函数公差的值测量接近于零，并且通过梯度测量问题显得有规律。
disp(规范(fval))
1.0657 e-09
disp (output.funcCount)
5005
这个解算器基本上得到了与之前相同的解，但需要进行数千次函数计算。
此代码创建nlsf1a函数。
函数F = nlsf1a(x)计算向量函数N =长度(x)F = 0 (n,1);I = 2:(n-1);F(i) = (3-2*x(i)).*x(i)-x(i-1)-2*x(i+1) +1;F(n) = (3-2*x(n)).*x(n)-x(n-1) + 1;F(1) = (3-2*x(1)).*x(1)-2*x(2) + 1;结束
另请参阅
相关的话题
您也可以从以下列表中选择一个网站:
