模拟股价 - Matlab＆Simulink - Mathwork金宝apps한국 - 金宝app,下载188bet金宝搏,金宝搏官方网站

模拟股票价格

模拟多维市场模型

这个例子比较了可分离的多元几何布朗运动过程的替代实现，通常被称为多维市场模式．它模拟了一个股票指数投资组合的样本路径钻，Sdeddo.，SDELD.，cev,GBM.对象。

模拟的市场模型为:

d X_{t} ＝ μ X_{t} d t + D （ X_{t} ） σ d W_{t}

（1）

地点:

μ是预期索引返回的对角线矩阵。
D对角矩阵是多少X_t沿着对角线。
σ是指数回报标准差的对角矩阵。

使用SDE对象表示市场模型

创建一个钻对象使用钻来表示股票市场模型。

加载data_globalidx2.数据集:

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];

将日常价格转换为退货：
```
回报= tick2ret(价格);
```

将数据统计信息计算为仿真方法：

nVariables = size(return, 2);expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);t = 0;X = 100;X = X ((nVariables, 1));

创建简单的匿名漂移和扩散功能（t，X_t）：

F = @(t,X) diag(expReturn) * X;g = @（t，x）诊断（x）* diag（sigma）;

使用以下函数钻创建一个钻对象表示的市场模型等式1：
```
sde = sde（f，g，“相关”的相关性,'startstate'， X）
```
```
SDE =类SDE：随机微分方程------------------------------------- 尺寸：状态= 6，布朗= 6 -------------------------------------------------- starttime：0 StartState：100（6x1双数组）相关性：6x6双阵列漂移：漂移率函数f（t，x（t））扩散：扩散速率g（t，x（t））仿真：仿真方法/功能SimByeuler
```
的钻对象需要其他信息来确定模型的维度，因为函数传递给钻物体仅通过它们（t，X_t）界面。换句话说，钻对象只需要两个输入:漂移率函数和扩散率函数，都可以通过通过采样时间和相应的状态向量(t，X_t）.
在这种情况下，这些信息不足以明确确定状态向量和布朗运动的维数。你可以通过指定一个初始状态向量来解决维度，StartState．SDE引擎已分配默认仿真方法，simByEuler,模拟范围。

使用SDEDDO对象代表市场模型

创建一个Sdeddo.对象使用Sdeddo.的市场模型等式1：

加载data_globalidx2.数据集:

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];

将日常价格转换为退货：
```
回报= tick2ret(价格);
```

将数据统计信息计算为仿真方法：

nVariables = size(return, 2);expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);

创建漂移和扩散对象的使用漂移和扩散：

f =漂移（零（nvariables，1），diag（expreturn））

A: 6x1双阵列B: 6x6对角线双阵列

g =扩散（那些（nvarialbles，1），diag（sigma））

G = Class DIFFUSION: DIFFUSION Rate Specification --------------------------------------------- Rate: DIFFUSION Rate function G(t,X(t)) Alpha: 6x1 double array Sigma: 6x6对角线double array

通过漂移和扩散对象Sdeddo.：
```
sdeddo = sdeddo（f，g，“相关”的相关性,......'startstate'，100）
```
```
SDE SDEDDO =类SDEDDO:从漂移和扩散对象  -------------------------------------------------- 维度:状态= 6,布朗= 6  -------------------------------------------------- 开始时间:0 StartState: 100 (6 x1双阵列)关系:6 x6双重数组漂移:漂移率函数F (t) X (t))扩散:模拟:模拟方法/函数simByEuler A: 6x1双阵B: 6x6对角双阵Alpha: 6x1双阵Sigma: 6x6对角双阵
```
的Sdeddo.对象需要两个输入对象，该对象提供比来自步骤4的两个功能更多的信息使用SDE对象表示市场模型．因此，维度更容易解决。实际上，每个索引的初始价格是标量（StartState＝100.）.这与钻对象，需要明确的状态向量，以唯一地确定问题的维度。
同样，每个对象的类都被清楚地标识，参数也像结构的字段一样显示。特别是,率将漂移和扩散对象的参数识别为时间和状态的可调用函数，f（t，x_t）和g（t，x_t）,分别。额外的参数,一个，B，Α,西格玛，为适当尺寸的数组，表示静态(非时变)参数。换句话说,X (t)_t），B (t) X_t），α(t, X_t）,sigma（t，x_t）是时间和状态的不变函数。

使用SDELD、CEV和GBM对象表示市场模型

创建SDELD.，cev,GBM.对象来表示市场模型等式1．

加载data_globalidx2.数据集:

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];

将日常价格转换为退货：
```
回报= tick2ret(价格);
```

将数据统计信息计算为仿真方法：

nVariables = size(return, 2);expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);t = 0;X = 100;X = X ((nVariables, 1));

创建一个SDELD.对象使用SDELD.：

SDELD = SDELD (0 (nVariables,1)， diag(expReturn)，......的(nVariables, 1),诊断接头(σ),“相关”，......相关性,'startstate'， X）

与线性漂移SDELD =类SDELD:钻  ---------------------------------------- 维度:状态= 6,布朗= 6  ---------------------------------------- 开始时间:0 StartState: 100 (6 x1双阵列)关系:6 x6双重数组漂移:漂移率函数F (t) X (t))扩散:扩散率函数G (t) X (t))模拟:simByEuler A: 6x1双阵B: 6x6对角线双阵Alpha: 6x1双阵Sigma: 6x6对角线双阵

创建一个cev对象使用cev：

CEV = CEV (diag(expReturn)， ones(nVariables,1)，......诊断（sigma），“相关”的相关性,......'startstate'， X）

cev = class cev：常量的异常弹性------------------------------------- 尺寸：状态= 6，布朗= 6 ------------------------------------------------  SignTime：0 StartState：100（6x1双数组）相关性：6x6双阵列漂移：漂移率函数f（t，x（t））扩散：扩散速率函数g（t，x（t））仿真：仿真方法/功能SimByeuler返回：6x6对角线双数组alpha：6x1双数组sigma：6x6对角线双数组

创建一个GBM.对象使用GBM.：

GBM = GBM (diag(expReturn)， diag(sigma)，“相关”，......相关性,'startstate'， X）

GBM =类GBM：广义几何布朗运动-------------------------------------------尺寸：状态= 6，布朗= 6 ---------------------------------------------------- Starttime：0 StartState：100（6x1双数组）相关性：6x6双阵列漂移：漂移率函数f（t，x（t））扩散：扩散速率函数g（t，x（t））仿真：仿真方法/功能SimByuuler返回：6x6对角线双数组Sigma：6x6对角线双数组

注意接口限制的连续性:

SDELD.对象要求您指定一个，B，Α,西格玛．
cev对象要求您指定返回，Α,西格玛．
GBM.对象只需要指定返回和西格玛．

然而，这三个对象代表了相同的多维市场模型。

还，cev和GBM.对象显示底层参数B来自于SDELD.对象返回．这是一个与股权模型共同关联的直观名称。

使用默认模拟方法模拟股票市场

加载data_globalidx2.数据集和使用钻来指定SDE模型使用SDE对象表示市场模型．

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];回报= tick2ret(价格);nvariables = size（返回，2）;expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);t = 0;X = 100;X = X ((nVariables, 1));f = @（t，x）诊断（expreturn）* x; G = @(t,X) diag(X) * diag(sigma); SDE = sde(F, G,“相关”，......相关性,'startstate', X);

使用默认值模拟一个日历年(定义为大约250个交易日)内相关股票指数价格的单一路径模拟方法：
```
nPeriods = 249;模拟观测的% #dt = 1;%时间增量= 1天rng (142857“旋风”）[s，t] =模拟（SDE，nperiods，'deltatime', dt);谁是年代
```
```
名称大小字节类属性S 250x6 12000双倍
```
输出数组年代是250×6 =（NPeriods + 1-经过-nvariables.-经过-1)数组具有相同的初始值，100.，用于所有索引。每一行的年代是对国家矢量的观察X_t在时间t．

绘制模拟路径。

情节(T, S),包含(“交易日”), ylabel (“价格”） 标题（“多维市场模式的单一路径”)({传奇“加拿大”'法国'“德国”“日本”'英国'“我们”}，......'地点'，“最佳”）

图中包含一个轴对象。以“多维市场模型的单一路径”为标题的轴对象包含6个线型对象。这些物体代表加拿大、法国、德国、日本、英国和美国。

使用SimByeuler方法模拟股票市场

因为simByEuler是一个有效的模拟方法，可以直接调用它，重写模拟参数的当前方法或函数(在本例中是simByEuler）.以下陈述会产生与生成的价格相同的价格路径使用默认模拟方法模拟股票市场：

加载data_globalidx2.数据集和使用钻来指定SDE模型使用SDE对象表示市场模型．

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];回报= tick2ret(价格);nvariables = size（返回，2）;expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);t = 0;X = 100;X = X ((nVariables, 1));f = @（t，x）诊断（expreturn）* x; G = @(t,X) diag(X) * diag(sigma); SDE = sde(F, G,“相关”，......相关性,'startstate', X);

使用。模拟单个路径simByEuler．

nPeriods = 249;模拟观测的% #dt = 1;%时间增量= 1天rng (142857“旋风”）[S，T] = SimByeuler（SDE，nperiods，'deltatime', dt);

在相同的初始条件下模拟10次试验，并进行检验年代：
```
rng (142857“旋风”）[s，t] =模拟（SDE，nperiods，'deltatime', dt,“nTrials”10);谁是年代
```
```
Name Size Bytes Class Attributes S 250x6x10 120000 double
```
现在输出数组年代是一个NPeriods + 1-经过-nvariables.-经过-ntrial时间序列数组。

绘制第一个路径。

情节(T, S(:,: 1)),包含(“交易日”), ylabel (“价格”） 标题（'多维市场模型的第一条路径')({传奇“加拿大”'法国'“德国”“日本”'英国'“我们”}，......'地点'，“最佳”）

图中包含一个轴对象。以“多维市场模型的第一条路径”为标题的坐标轴对象包含6个线型对象。这些物体代表加拿大、法国、德国、日本、英国和美国。

第一次意识到年代和图中的路径是一样的。

使用GBM仿真方法模拟股票市场

最后，考虑使用模拟GBM.仿真方法。可分GBM.模型有两种具体的仿真方法:

超载的欧拉仿真方法，simByEuler，为最佳性能而设计
一个函数,simBySolution，提供了潜在的随机微分方程的近似解，为精度而设计

加载data_globalidx2.数据集和使用钻来指定SDE模型使用SDE对象表示市场模型和GBM模型一样使用SDELD、CEV和GBM对象表示市场模型．

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];回报= tick2ret(价格);nvariables = size（返回，2）;expReturn =意味着(回报);σ=性病(回报);相关= corrcoef(回报);t = 0;X = 100;X = X ((nVariables, 1));f = @（t，x）诊断（expreturn）* x; G = @(t,X) diag(X) * diag(sigma); SDE = sde(F, G,“相关”，......相关性,'startstate', X);“绿带运动”=“绿带运动”(诊断接头(expReturn)诊断接头(σ),“相关”，......相关性,'startstate', X);

为了说明重载欧拉近似方法的性能优势，将试验次数增加到10000．

nPeriods = 249;模拟观测的% #dt = 1;%时间增量= 1天rng (142857“旋风”）[x，t] =模拟（gbm，nperiods，'deltatime', dt,......“nTrials”, 10000);谁是X

名称大小字节类属性x 250x6x10000 120000000双倍

输出X是一个更大的时间序列阵列。

使用此示例大小，检查加拿大TSX复合材料的终端分布，以定性地验证数据的逻辑字符。

直方图(挤压(X(1,:)), 30),包含(“价格”), ylabel (“频率”） 标题（'一年后价格的直方图：加拿大（TSX Composite）'）

图中包含一个轴对象。标题为“一年之后的价格直方图:加拿大(TSX Composite)”的轴对象包含一个直方图类型的对象。

模拟解决方案的10次试验，并绘制第一次试验:

rng (142857“旋风”）[s，t] =模拟（SDE，nperiods，'deltatime', dt,“nTrials”10);rng (142857“旋风”) [X,T] = simBySolution(GBM, nPeriods，......'deltatime', dt,“nTrials”10);子图（2,1,1）绘图（t，s（：，：，1）），xlabel（“交易日”），ylabel（“价格”） 标题（'多重暗淡市场模型的第1条路径：欧拉近似')子plot(2,1,2) plot(T, X(:，: 1))， xlabel(“交易日”），ylabel（“价格”） 标题（“多元暗淡市场模型的第一条路径:解析解”）

图中包含2个轴对象。轴对象1，标题为“多重昏暗市场模型路径1:欧拉近似”，包含6个类型为线的对象。轴对象2，题目为“多元市场模型路径1:解析解”，包含6个线型对象。

在这个例子中，所有的参数都是常数simBySolution确实取样了精确的溶液。任何给定试验的单个指数的细节表明，欧拉近似的价格路径和精确解是接近的，但不相同。

下图说明了这两种方法的区别:

plot(T, S(:，1,1) - X(:，1,1)，'蓝色'）， 网格（“上”）Xlabel（“交易日”), ylabel ('差价'） 标题（'欧拉大约减去精确解决方案：加拿大（TSX Composite）'）

图中包含一个轴对象。具有标题欧拉大约减去精确解决方案的轴对象：加拿大（TSX复合材料）包含类型线的对象。

的simByEuler欧拉近似字面上直接从运动方程计算随机微分方程，为一些合适的值dt时间增量。这种简单的近似遭受了离散化错误。此错误归因于所选选择之间的差异dt时间递增，理论上是什么是连续时间参数。

离散时间近似提高了DeltaTime接近零。欧拉法通常是最不精确和最通用的方法。仿真套件中的所有模型都有这个方法。

相比之下，simBySolution方法提供了对底层模型的更准确的描述。该方法通过对可分离模型的封闭解的近似来模拟价格路径。具体地说，它将欧拉方法应用到变换过程中，这通常不是这个问题的确切解GBM.模型。这是因为只有对于分段常数参数，模拟的状态向量和真实状态向量的概率分布是相同的。

当所有模型参数在每个观测周期内都是分段常数时，模拟过程对于采样状态向量的观测时间是精确的。由于本例中所有参数都是常量，simBySolution确实取样了精确的溶液。

以举例说明如何使用simBySolution要优化解的精度，请参阅金宝搏官方网站优化精度:关于解的精度和误差．

诱导依赖性和相关性

这个示例演示了两种诱导状态向量的各个元素之间的依赖关系的技术。它也说明了西格玛和相关．

第一种方法是生成相关高斯变量，形成具有相关分量的布朗运动过程。然后用对角波动率或敞口矩阵对这些成分进行加权西格玛．

第二种技术产生独立的高斯变量，形成一个标准的布朗运动过程，然后由所需协方差矩阵的较低的Cholesky因子加权。尽管这些技术可以用于许多模型，但它们之间的关系最容易通过使用可分离模型来说明GBM.模型(见使用GBM仿真方法模拟股票价格）.模拟的市场模型为:

$d X_{t} ＝ μ X_{t} d t + σ X_{t} d W_{t}$

在哪里μ是一个对角矩阵。

加载数据集:

负载data_globalidx2.价格= [dataset.tsx dataset.cac dataset.dax......dataset.nik dataset.fse dataset.sp];

将每日价格转换为回报:
```
回报= tick2ret(价格);
```
指定西格玛和相关使用第一种技术:
1. 使用第一种技术，指定西格玛作为资产收益标准差的对角矩阵:
  expReturn =诊断接头(意味着(回报));％预期回报载体sigma = diag（std（returns））;回报率波动率
2. 指定相关作为这些回报的样本相关矩阵。在这种情况下，布朗运动的分量是相关的:
  相关= corrcoef(回报);GBM1 = GBM（Expreturn，Sigma，“相关”，......相关);
指定西格玛和相关使用第二种技巧:
1. 使用第二种技术，指定西格玛作为资产返回协方差矩阵的较低弦因因素：
  协方差= x(回报);协方差σ= cholcov()”;
2. 集相关到身份矩阵：
  GBM2 =“绿带运动”(expReturn,σ);
  这里，σ捕捉资产回报不确定性的相关性和大小。与第一种方法不同，布朗运动的各分量是独立的。此外，该技术接受单位矩阵的默认赋值相关，并且更直接。

使用这两种技术模拟1000个观察（大约四年的日常数据）的单一试验。默认情况下，所有状态变量都已开始1：

RNG（22814，“旋风”) [X1,T] = simByEuler(GBM1,1000);%相关布朗运动RNG（22814，“旋风”）[x2，t] = simbyuular（gbm2,1000）;%标准布朗运动

基于相同的初始随机数状态时，每个技术会产生相同的资产价格路径：

子图（2,1,1）绘图（T，x1）标题（“相关布朗运动的样本路径”) ylabel ('资产价格'）子图（2,1,2）绘图（T，x2）标题（'标准布朗运动的样品路径'）Xlabel（“交易日”) ylabel ('资产价格'）

图中包含2个轴对象。标题为“相关布朗运动的样本路径”的轴对象1包含6个类型为line的对象。标题为“标准布朗运动的样本路径”的轴对象2包含6个类型为line的对象。

市场参数的动态行为

讨论了在创建数据对象，可以评估对象参数，就好像它们是matlab一样^®通用接口可访问的功能。这种可访问性提供了动态行为的印象，而不管底层参数是否真的是时变的。此外，由于参数可以通过公共接口访问，表面上简单的线性结构实际上可能代表复杂的非线性设计。

例如，考虑以下形式的单变量几何布朗运动(GBM)模型:

$d X_{t} ＝ μ （ t ） X_{t} d t + σ （ t ） X_{t} d W_{t}$

在这个模型中，回归，μ（T）波动,σ(t)，仅是时间的动态参数。然而，当创建GBM.对象表示底层模型，必须通过常见（t，X_t）界面。这反映了这一事实GBM.模型（和其他）是来自常规的受限参数化钻班级。

方便的是，您可以指定受限制模型的参数，例如GBM.模型，作为传统MATLAB阵列的适当维度。在这种情况下，这种阵列代表了一种静态特殊情况，可以通过（t，X_t）界面。

此外，当您将参数作为函数输入时，对象构造函数可以通过在初始时间和初始状态计算它们来验证它们是否返回大小正确的数组。否则，对象构造函数不知道任何特定的函数形式。

以下示例说明了一种技术，该技术包括通过将传统的MATLAB时间序列阵列映射到可调用函数的动态行为（t，X_t）界面。它还将函数与恒定参数的恒定参数进行比较。

因为时间序列数组表示的是动态行为，必须由(t，X_t）接口，您需要实用程序将传统的时间序列阵列转换为可调用的时间和状态函数。以下示例显示了如何使用转换函数执行此操作ts2func(时间序列的功能)。

加载数据。加载日常历史数据集，其中包含三个月的EURIBOR率和收盘指数水平法国CAC 40跨越2001年2月7日至2006年4月24日的时间间隔：
```
负载data_globalidx2.
```
模拟风险中性的样本路径。利用几何布朗运动模拟CAC 40指数的风险中性样本路径(GBM.）模型：

$d X_{t} ＝ r （ t ） X_{t} d t + σ X_{t} d W_{t}$

在哪里r（t）代表无风险回报率的演变。
此外，假设您需要将从每日数据中获得的相关信息按年计算(按年计算数据是可选的，但在与其他例子比较时很有用)，并且每个日历年包含250个交易日:
```
dt = 1/250;returns = tick2ret（dataset.cac）;sigma = std（返回）* sqrt（250）;产量= dataset.eb3m;产量= 360 * log（1 +产量）;
```
比较两种风险中性历史模拟方法的样本路径。比较两种风险中性历史模拟方法得到的样本路径，其中欧元银行间同业拆借利率(Euribor)日收益率作为无风险收益率的代理。
1. 第一种方法将风险中性回报指定为Euribor收益率的样本平均值，因此假设无风险回报为常数(非动态):
  nperiods =长度（产量）;%模拟观测RNG（5713，“旋风”) obj = gbm(mean(yield)，diag(sigma)，'startstate', 100)
  obj =类GBM:广义几何布朗运动 ------------------------------------------------ 维度:状态= 1,布朗= 1 ------------------------------------------------ 开始时间:0 StartState: 100相关:1漂移:漂移率函数F (t) X (t))扩散:扩散率函数G (t) X (t))模拟:返回值:0.0278117 Sigma: 0.231906
  [x1，t] =模拟（obj，nperiods，'deltatime', dt);
2. 相比之下，第二种方法将风险中性回报指定为欧元银行间同业拆借利率(Euribor)收益率的历史时间序列。因此，它假设一个动态的，但确定的回报率;这个例子没有说明随机利率。为了说明这种动态效果，可以使用ts2func用途:
  r = ts2func(产量,“次”，（0：nperiods - 1）'）;
  ts2func将指定的时间序列数组封装在可调用的时间和状态函数中，并与可选的时间向量进行同步。例如:
  r（0,100）
  ans = 0.0470
  评估（t= 0,X_t= 100）并返回首次观察到的EURIBOR产量。但是，您还可以在任何中间时间评估结果函数t和州X_t：
  r（7.5,200）
  ans = 0.0472
  此外，以下命令在单独调用时产生相同的结果：
  r（7.5）
  ans = 0.0472
  最后两个命令的等价性突出了一些重要特性。
  当将参数指定为函数时，它们必须在传递标量、实值采样时间(t），和据nvar-经过-1州矢量（X_t）.它们还必须生成一个适当的维数数组，在第一种情况下是一个标量常数，在第二种情况下是一个标量，单独的时间分段常数函数。
  您不需要使用任何时间（t）或州（X_t）.在当前的示例中，当经过的时间后跟状态时，该函数将正确计算，从而满足最小需求。当只经过时间时，它也能正确计算，这一事实只是表明函数不需要状态向量X_t．要做的重要点是当你通过它时它会工作（t，X_t）.
  此外,ts2func函数执行零阶保持(ZOH)分段常数插值。分段常数参数的概念在整个SDE体系结构中很普遍，在下文中将进行更详细的讨论优化精度:关于解的精度和误差．

使用相同的初始随机数状态执行第二次模拟。通过使用相同的初始随机数状态执行第二次模拟来完成比较:

RNG（5713，“旋风”) obj = gbm(r, diag(sigma)，'startstate', 100)

obj =类GBM:广义几何布朗运动  ------------------------------------------------ 维度:状态= 1,布朗= 1  ------------------------------------------------ 开始时间:0 StartState: 100相关:1漂移:漂移率函数F (t) X (t))扩散:扩散率函数G (t) X (t))模拟:返回:函数ts2func/vector2Function Sigma: 0.231906

X2 =模拟(obj, nPeriods'deltatime', dt);

比较两个模拟试验。绘制无风险参考率序列，以比较两个模拟试验:

子图（2,1,1）绘图（日期，100 *收益率）DateTick（“x”）Xlabel（“日期”) ylabel ('年化产量（％）'） 标题（'无风险费率（3-Mo Euribor不断复合）'次要情节(2,1,2)情节(T, X1,“红色”, T, X2,'蓝色'）Xlabel（'时间（年）') ylabel (“指数级”） 标题（“恒定收益率与动态收益率:CAC 40”)({传奇'不断利率''动态利率'}，......'地点'，“最佳”）

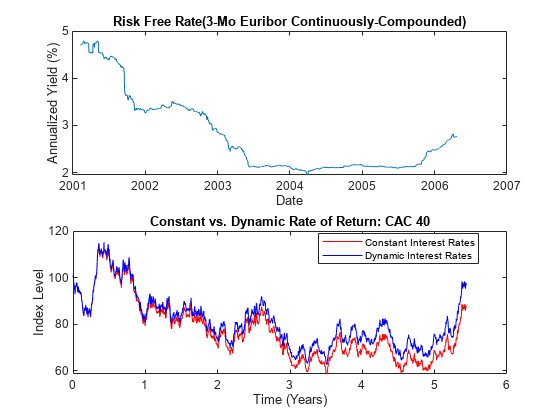
图中包含2个轴对象。轴对象1，标题为无风险利率(3-Mo Euribor连续复合)，包含一个类型为线的对象。轴对象2的标题为常量vs.动态回报率:CAC 40包含2个类型为line的对象。这些对象代表恒定利率，动态利率。

这些路径很近，但并不精确。最后一个图中的蓝线使用了所有的历史Euribor数据，并说明了历史模拟的单个试验。

股票期权定价

讨论了在确保积极的利率，所有的模拟和插值方法都允许您指定表单的一个或多个函数:

$X_{t} ＝ f （ t ， X_{t} ）$

在每个采样时间结束时评估。

相关的示例演示了一个简单、常见的期末处理函数，以确保非负利率。这个示例演示了一个处理函数，它允许您完全避免模拟输出。

考虑在Black-Scholes-Merton框架内通过Monte Carlo仿真定价欧洲股票期权。假设库存具有以下特征：

该股目前交易100。
该股票不支付股息。
该股每年的波动性为50%。
期权罢工价格为95。
期权三个月后到期。
无风险率为每年10％恒定。

要解决这个问题，通过恒定参数模拟单变量几何褐色运动（GBM）模型的底层库存的演变：

$d X_{t} ＝ 0.1 X_{t} d t + 0.5 X_{t} d W_{t}$

此外，假设每天模拟股价，每个日历月都包括21个交易日：

罢工= 95;速率= 0.1;Sigma = 0.5;dt = 1/252;nperiods = 63;t = nperiods * dt;obj = gbm（速率，sigma，'startstate', 100);

目标是模拟每日股票价格的独立路径，并计算欧洲期权的价格，作为从现在算起的63天到期时贴现的终端期权支付的风险中性样本平均值。这个例子通过两种方法计算期权价格:

一个蒙特卡罗模拟，明确要求模拟的储存路径作为输出。然后使用输出路径来价格为选项。
一个周期结束处理函数，可通过时间和状态访问，记录每个样本路径的终端股票价格。这个处理函数是作为一个嵌套函数实现的，可以访问共享信息。有关更多信息，请参见example_blackscholes.m.．

在模拟之前，调用示例文件来访问句号处理函数:

ntrials = 10000;％独立试验数量（即，路径）f = Example_BlackScholes (nPeriods nTrials)

F =结构体字段:blackscholes：@ exalde_blackscholes / saveterminalstockprice callprice：@ example_blackscholes / getcallprice putprice：@ example_blackscholes / getputprice

模拟10000个独立试验(样本路径)。请求模拟的股价路径作为输出，并指定周期结束处理函数:

rng (88161“旋风”X = simBySolution(obj,nPeriods，'deltatime'，dt，......“nTrials”nTrials,“过程”, f.BlackScholes);

直接从模拟的股票价格路径计算期权价格。因为这些是欧洲期权，所以忽略所有中间股票价格:

调用=意味着(exp(率* T *马克斯(挤压(X(:,:)),罢工,0))

电话= 13.9342

PUT =均值（EXP（-Rate * T）* MAX（Strike  -  Squeeze（x（x（结束，：，:)），0）））

把= 6.4166

通过调用嵌套函数来间接为选项定价:
```
f.CallPrice(罢工,率)
```
```
ans = 13.9342
```
```
f.PutPrice(罢工,率)
```
```
ans = 6.4166
```
作为参考，根据布莱克-斯科尔斯期权公式计算的理论看涨和看跌价格为13.6953和6.3497,分别。
虽然步骤3和步骤4产生相同的期权价格，但后一种方法直接与每个样本路径的终端股票价格一起工作。因此，它的内存效率更高。在本例中，没有强制要求输出的理由。