试用软件

试用软件

产品更新

产品更新

关于行业界限和行业指数

打开生活的脚本

圆锥扇形

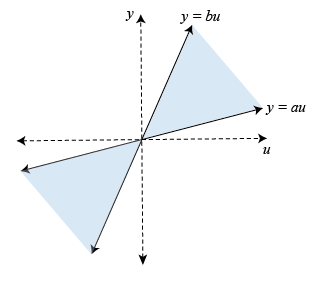
在最简单的形式中，圆锥扇形是由两条线划定的二维区域， $Y = A. U$ 和 $Y = B U$ ．

阴影区域的特征是不平等 $(Y - A. U) (Y - B U) < 0$ 。更一般而言，任何此类部门均可参数化为：

${(\begin{array}{c} Y \\ U \end{array})}^{T} Q (\begin{array}{c} Y \\ U \end{array}) < 0,$

哪里 $Q$ 是一个2x2对称不定矩阵( $Q$ 有一个正的和一个负的特征值)。我们称之为 $Q$ 这个扇区矩阵。这个概念推广到更高维。在N维空间中，圆锥扇形是一个集合：

$s = {Z \in R^{N} : Z^{T} Q Z < 0},$

哪里 $Q$ 还是一个对称不定矩阵。

扇区界限

扇区边界是对系统行为的约束。增益约束和无源约束是扇区边界的特殊情况。对于所有非零输入轨迹 $U (T)$ ，输出轨迹 $Z (T) = (H U) (T)$ 线性系统的稳定性 $H (s)$ 满足:

$\int_{0}^{T} Z^{T} (T) Q Z (T) D T < 0, \forall T > 0,$

然后输出轨迹 $H$ 位于带矩阵的二次曲线扇形内 $Q$ . 选择不同的 $Q$ 矩阵对系统的响应施加不同的条件。例如，考虑轨迹。 $Y (T) = (G U) (T)$ 以及以下值：

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array}) ．$

这些值对应于扇区界限：

$\int_{0}^{T} {(\begin{array}{c} Y (T) \\ U (T) \end{array})}^{T} (\begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array}) (\begin{array}{c} Y (T) \\ U (T) \end{array}) D T < 0, \forall T > 0 ．$

这个扇形界等价于 $G (s)$ :

$\int_{0}^{T} Y^{T} (T) U (T) D T > 0, \forall T > 0 ．$

换句话说，被动性是系统上的一个特定区域，定义为:

$H = (\begin{array}{c} G \\ 我 \end{array}) ．$

频域条件

因为时域条件必须适用于所有情况 $T > 0$ 在美国，推导一个等效的频域界限需要一点小心，而且并不总是可能的。让下面的:

$Q = W_{1.}^{T} W_{1.} - W_{2.}^{T} W_{2.}$

是不定矩阵的(任意)分解 $Q$ 它的积极和消极部分。当 $W_{2.}^{T} H (s)$ 为平方和最小相位（无不稳定零点），时域条件：

$\int_{0}^{T} (H U) (T)^{T} Q (H U) (T) D T < 0, \forall T > 0$

等效于频域条件：

$H (J ω)^{H} Q H (J ω) < 0 \forall ω \in R ．$

因此，检查实际频率的扇区不平等就足够了。通过分解 $Q$ ，这也相当于:

${‖ (W_{1.}^{T} H) (W_{2.}^{T} H)^{- 1.} ‖}_{\infty} < 1. ．$

注意 $W_{2.}^{T} H$ 什么时候是正方形的 $Q$ 有和输入通道一样多的负特征值 $H (s)$ 。如果不满足此条件，则（通常）仅查看真实频率是不够的。还要注意，如果 $W_{2.}^{T} H (s)$ 如果是正方形，则它必须是扇区绑定保持的最小相位。

这种频域特性是分析的基础sectorplot．具体地说,sectorplot绘制 $(W_{1.}^{T} H (J ω)) (W_{2.}^{T} H (J ω))^{- 1.}$ 作为频率的函数。当且仅当最大奇异值保持在1以下时才满足扇形界。此外，该图包含有关满足或违反扇形界的频带以及满足或违反扇形界的程度的有用信息。

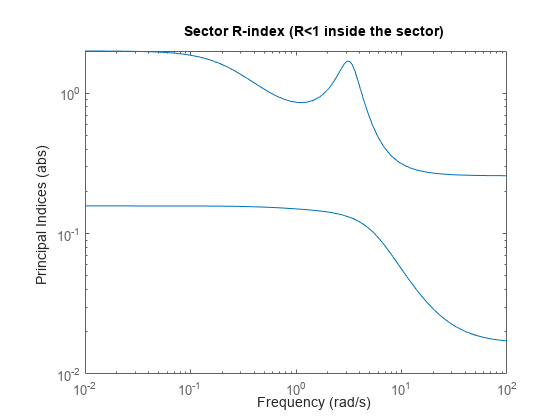
例如，检查特定扇区的2输出2输入系统的扇区图。

rng (4“龙卷风”）;H = rss(3、4、2);Q = [-5.12 2.16 -2.04 2.17 2.16 -1.22 -0.28 -1.11 -2.04 -0.28 -3.35 0.00 2.17 -1.11 0.00 - 0.18);sectorplot (H, Q)

图中包含一个轴对象。轴对象包含两个line类型的对象。此对象表示H。

图中显示了 $(W_{1.}^{T} H (J ω)) (W_{2.}^{T} H (J ω))^{- 1.}$ 在0.5 rad/s以下超过1，在3 rad/s左右的窄带内超过1。因此,H不满足由表示的扇区界限Q．

相对行业指数

我们可以将相对被动性指数的概念扩展到任意扇区。允许 $H (s)$ 是一个LTI系统，让:

$Q = W_{1.}^{T} W_{1.} - W_{2.}^{T} W_{2.}, W_{1.}^{T} W_{2.} = 0$

的正交分解 $Q$ 转化为它的积极部分和消极部分，这是很容易从舒尔分解得到的 $Q$ ．的相对行业指数 $R$ ，或R-index，定义为最小的 $R > 0$ 对于所有的输出轨迹 $Z (T) = (H U) (T)$ :

$\int_{0}^{T} Z^{T} (T) (W_{1.}^{T} W_{1.} - R^{2.} W_{2.}^{T} W_{2.}) Z (T) D T < 0, \forall T > 0 ．$

因为增加 $R$ 制造 $W_{1.}^{T} W_{1.} - R^{2.} W_{2.}^{T} W_{2.}$ 更为消极的是，不等式通常满足于 $R$ 足够大。但是，在某些情况下，它永远无法满足，在这种情况下，R指数是 $R = + \infty$ ．显然，当且仅当时，原始扇区边界满足 $R \leq 1.$ ．

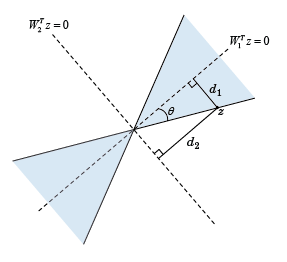
为了理解R指数的几何解释，考虑矩阵的锥族。 $Q (R) = W_{1.}^{T} W_{1.} - R^{2.} W_{2.}^{T} W_{2.}$ ．在2D中，圆锥的倾斜角 $θ$ 有关 $R$ 通过

$棕褐色 (θ) = R \frac{‖ W_{2.} ‖}{‖ W_{1.} ‖}$

(见下面的图)。更普遍的是, $棕褐色 (θ)$ 成正比 $R$ 因此，给定一个带矩阵的二次曲线扇形 $Q$ ， r指标值 $R < 1.$ 意味着我们可以减少 $棕褐色 (θ)$ (把圆锥体缩小)一个倍数 $R$ 在一些输出轨迹之前 $H$ 离开圆锥扇区。同样,一个值 $R > 1.$ 意味着我们必须增加 $棕褐色 (θ)$ (把圆锥体加宽)一倍 $R$ 的所有输出轨迹 $H$ ．这显然使r指数成为一个相对衡量的反应如何 $H$ 适合于特定的圆锥扇形。

在图表中，

$D_{1.} \frac{| W_{1.}^{T} Z |}{‖ W_{1.} ‖}, D_{2.} \frac{| W_{2.}^{T} Z |}{‖ W_{2.} ‖}, R = \frac{| W_{1.}^{T} Z |}{| W_{2.}^{T} Z |},$

和

$棕褐色 (θ) = \frac{D_{1.}}{D_{2.}} = R \frac{‖ W_{2.} ‖}{‖ W_{1.} ‖} ．$

当 $W_{2.}^{T} H (s)$ 是平方和最小相位，R指数也可以在频域中表征为最小 $R > 0$ 这样:

$H (J ω)^{H} (W_{1.}^{T} W_{1.} - R^{2.} W_{2.}^{T} W_{2.}) H (J ω) < 0 \forall ω \in R ．$

使用初等代数，可以得到:

$R = \underset{ω}{马克斯} ‖ (W_{1.}^{T} H (J ω)) (W_{2.}^{T} H (J ω))^{- 1.} ‖ ．$

换句话说，R指数是（稳定）传递函数的峰值增益 $Φ (s) : = (W_{1.}^{T} H (s)) (W_{2.}^{T} H (s))^{- 1.}$ 的奇异值 $Φ (J W)$ 可以被视为每个频率的“主要”R指数。这也解释了为什么绘制R指数与频率的关系图看起来像是奇异值图（参见sectorplot）.相对扇区指数与系统增益具有完全的相似性。然而，请注意，这种类比只适用于以下情况 $W_{2.}^{T} H (s)$ 为方形，最小相位。

定向行业指数

同样，我们可以将方向无源性指数的概念推广到任意扇区。给出一个带矩阵的圆锥扇形 $Q$ ，一个方向 $δ Q$ ，其中指向性板块指数最大 $τ$ 对于所有的输出轨迹 $Z (T) = (H U) (T)$ :

$\int_{0}^{T} Z^{T} (T) (Q + τ δ Q) Z (T) D T < 0, \forall T > 0 ．$

一个系统的定向无源性指标 $G (s)$ 对应:

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array}) ．$

方向扇区指数衡量我们需要在方向上使扇区变形多少 $δ Q$ 让它紧紧地围绕着输出轨迹 $H$ ．当且仅当指向性指数为正值时，行业界限是满足的。

常见的行业

有很多方法可以指定扇区边界。接下来我们将回顾常见的表达式并给出相应的系统 $H$ 和部门矩阵 $Q$ 对于所使用的标准表格getSectorIndex和sectorplot:

$\int_{0}^{T} (H U) (T)^{T} Q (H U) (T) D T < 0, \forall T > 0 ．$

为简单起见，这些描述使用以下符号：

$‖ x ‖_{T} = \int_{0}^{T} ‖ x (T) ‖^{2.} D T,$

和省略 $\forall T > 0$ 要求。

被动

被动性是一个与:

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array}) ．$

增益约束

获得约束 ${‖ G ‖}_{\infty} < γ$ 一个部门是否与以下方面有关：

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 我 & 0 \\ 0 & - γ^{2.} 我 \end{array}) ．$

距离的比例

考虑“内部”约束，

$‖ Y - C U ‖_{T} < R ‖ U ‖_{T}$

哪里 $C, R$ 标量和 $Y (T) = (G U) (T)$ 。这是一个与以下方面有关的行业：

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 我 & - C 我 \\ - C 我 & (C^{2.} - R^{2.}) 我 \end{array}) ．$

下面的二次曲线扇形是对称的 $Y = C U$ .同样，“外部”约束，

$‖ Y - C U ‖_{T} > R ‖ U ‖_{T}$

一个部门是否与以下方面有关：

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} - 我 & C 我 \\ C 我 & (R^{2.} - C^{2.}) 我 \end{array}) ．$

双重不平等

在处理静态非线性时，通常考虑圆锥形扇形。

$A. U^{2.} < Y U < B U^{2.},$

哪里 $Y = ϕ (U)$ 是非线性输出。虽然这种关系本身不是扇区界限，但它清楚地表明：

$A. \int_{0}^{T} U (T)^{2.} D T < \int_{0}^{T} Y (T) U (T) D T < B \int_{0}^{T} U (T)^{2.} D T$

沿着所有的I/O轨迹 $T > 0$ .此条件反过来相当于与以下条件绑定的扇区：

$H (s) = (\begin{array}{c} ϕ (．) \\ 1. \end{array}), Q = (\begin{array}{cc} 1. & - (A. + B) / 2. \\ - (A. + B) / 2. & A. B \end{array}) ．$

产品形式

形式的广义扇形界：

$\int_{0}^{T} (Y (T) - K_{1.} U (T))^{T} (Y (T) - K_{2.} U (T)) D T < 0$

对应于：

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = (\begin{array}{cc} 2. 我 & - (K_{2.} + K_{1.}^{T}) \\ - (K_{1.} + K_{2.}^{T}) & K_{1.}^{T} K_{2.} + K_{2.}^{T} K_{1.} \end{array}) ．$

如前所述，静态扇区边界:

$(Y - K_{1.} U)^{T} (Y - K_{2.} U) < 0$

表示上面的整数扇形界。

近年耗散

一个系统 $Y = G U$ 是qsr耗散的，如果满足:

$\int_{0}^{T} {(\begin{array}{c} Y (T) \\ U (T) \end{array})}^{T} (\begin{array}{cc} Q & s \\ s^{T} & R \end{array}) (\begin{array}{c} Y (T) \\ U (T) \end{array}) D T > 0, \forall T > 0 ．$

这是一个与:

$H (s) = (\begin{array}{c} G (s) \\ 我 \end{array}), Q = - (\begin{array}{cc} Q & s \\ s^{T} & R \end{array}) ．$

另见

getSectorIndex|sectorplot|getSectorCrossover

关于行业界限和行业指数

圆锥扇形

扇区界限

频域条件

相对行业指数

定向行业指数

常见的行业

另见

相关的话题

控制系统工具箱文档

金宝app

学习如何自动调整PID控制器增益