This is a follow-up tomy previous post.Classical Gram-Schmidt and Modified Gram-Schmidt are two algorithms for orthogonalizing a set of vectors. Householder elementary reflectors can be used for the same task. The three algorithms have very different roundoff error properties.

Contents

Pete Stewart

As I did in my previous post, I am using Pete Stewart's bookMatrix Algorithms, Volume I: Basic Decompositions. His pseudocode is MATLAB ready.

Classic Gram-Schmidt

The classic Gram-Schmidt algorithm is the first thing you might think of for producing an orthogonal set of vectors. For each vector in your data set, remove its projection onto the data set, normalize what is left, and include it in the orthogonal set. Here is the code.Xis the original set of vectors,Qis the resulting set of orthogonal vectors, andRis the set of coefficients, organized into an upper triangular matrix.

typegs

function [Q,R] = gs(X) % Classical Gram-Schmidt. [Q,R] = gs(X); % G. W. Stewart, "Matrix Algorithms, Volume 1", SIAM, 1998. [n,p] = size(X); Q = zeros(n,p); R = zeros(p,p); for k = 1:p Q(:,k) = X(:,k); if k ~= 1 R(1:k-1,k) = Q(:,k-1)'*Q(:,k); Q(:,k) = Q(:,k) - Q(:,1:k-1)*R(1:k-1,k); end R(k,k) = norm(Q(:,k)); Q(:,k) = Q(:,k)/R(k,k); end end

Modified Gram-Schmidt

这是一个相当不同的算法,不仅仅是一个年代imple modification of classical Gram-Schmidt. The idea is to orthogonalize against the emerging set of vectors instead of against the original set. There are two variants, a column-oriented one and a row-oriented one. They produce the same results, in different order. Here is the column version,

typemgs

function [Q,R] = mgs(X) % Modified Gram-Schmidt. [Q,R] = mgs(X); % G. W. Stewart, "Matrix Algorithms, Volume 1", SIAM, 1998. [n,p] = size(X); Q = zeros(n,p); R = zeros(p,p); for k = 1:p Q(:,k) = X(:,k); for i = 1:k-1 R(i,k) = Q(:,i)'*Q(:,k); Q(:,k) = Q(:,k) - R(i,k)*Q(:,i); end R(k,k) = norm(Q(:,k))'; Q(:,k) = Q(:,k)/R(k,k); end end

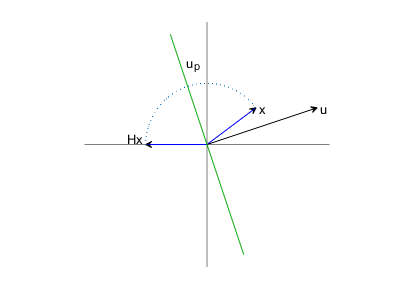
Householder Reflections

ComputeRby applying Householder reflections toXa column at a time. Do not actually computeQ, just save the vectors that generate the reflections. See the description and codes frommy previous post.

typehouse_qr

function [U,R] = house_qr(A) % Householder reflections for QR decomposition. % [U,R] = house_qr(A) returns % U, the reflector generators for use by house_apply. % R, the upper triangular factor. H = @(u,x) x - u*(u'*x); [m,n] = size(A); U = zeros(m,n); R = A; for j = 1:min(m,n) u = house_gen(R(j:m,j)); U(j:m,j) = u; R(j:m,j:n) = H(u,R(j:m,j:n)); R(j+1:m,j) = 0; end end

Comparison

For various matricesX, let's check how the three algorithms perform on two tasks, accuracy and orthogonality. How close isQ*RtoX? And, how close isQ'*QtoI.

typecompare.m

function compare(X); % compare(X). Compare three QR decompositions. I = eye(size(X)); qrerr = zeros(1,3); ortherr = zeros(1,3); %% Classic Gram Schmidt [Q,R] = gs(X); qrerr(1) = norm(Q*R-X,inf)/norm(X,inf); ortherr(1) = norm(Q'*Q-I,inf); %% Modified Gram Schmidt [Q,R] = mgs(X); qrerr(2) = norm(Q*R-X,inf)/norm(X,inf); ortherr(2) = norm(Q'*Q-I,inf); %% Householder QR Decomposition [U,R] = house_qr(X); QR = house_apply(U,R); QQ = house_apply_transpose(U,house_apply(U,I)); qrerr(3) = norm(QR-X,inf)/norm(X,inf); ortherr(3) = norm(QQ-I,inf); %% Report results fprintf('\n Classic Modified Householder\n') fprintf('QR error %10.2e %10.2e %10.2e\n',qrerr) fprintf('Orthogonality %10.2e %10.2e %10.2e\n',ortherr)

Well conditioned.

First, try a well conditioned matrix, a magic square of odd order.

n = 7; X = magic(n)

X = 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 11 20

检查它的状态。

kappa = condest(X)

kappa = 8.5681

Do the comparison.

compare(X);

Classic Modified Householder QR error 1.73e-16 6.09e-17 5.68e-16 Orthogonality 3.20e+00 1.53e-15 1.96e-15

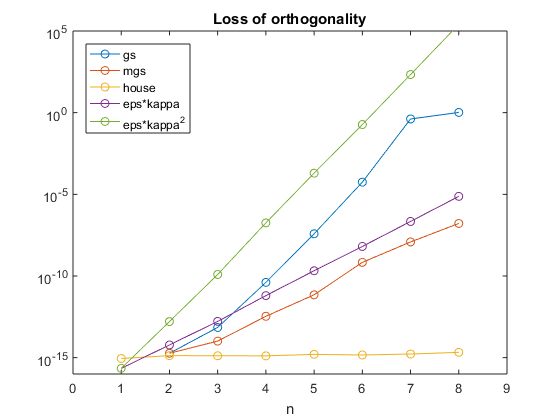
All three algorithms do well with accuracy, but classic Gram-Schmidt fails with orthogonality.

Poorly conditioned.

Next, try a Hilbert matrix that is poorly conditioned, but not exactly singular.

n = 7; X = hilb(n)

X = 1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.0833 0.1429 0.1250 0.1111 0.1000 0.0909 0.0833 0.0769

检查它的状态。

kappa = condest(X)

kappa = 9.8519e+08

Do the comparison.

compare(X)

Classic Modified Householder QR error 5.35e-17 5.35e-17 8.03e-16 Orthogonality 5.21e+00 1.22e-08 1.67e-15

All three algorithms do well with accuracy. Classic Gram-Schmidt fails completely with orthogonality. The orthogonality of MGS depends uponkappa. Householder does well with orthogonality.

单数。

Finally, an exactly singular matrix, a magic square of even order.

n = 8; X = magic(n)

X = 64 2 3 61 60 6 7 57 9 55 54 12 13 51 50 16 17 47 46 20 21 43 42 24 40 26 27 37 36 30 31 33 32 34 35 29 28 38 39 25 41 23 22 44 45 19 18 48 49 15 14 52 53 11 10 56 8 58 59 5 4 62 63 1

Check its rank.

rankX = rank(X)

rankX = 3

Do the comparison.

compare(X)

Classic Modified Householder QR error 1.43e-16 8.54e-17 4.85e-16 Orthogonality 5.41e+00 2.16e+00 1.30e-15

Again, all three algorithms do well with accuracy. Both Gram-Schmidts fail completely with orthogonality. Householder still does well with orthogonality.

Conclusion

All three of these algorithms provideQandRthat do a good job of reproducing the dataX, that is

On the other hand, their behavior is very different when it comes to producing orthogonality.

Reference

G. W. Stewart,Matrix Algorithms: Volume 1: Basic Decompositions, SIAM, xix+458, 1998.>

Get the MATLAB code

Published with MATLAB® R2016a